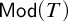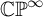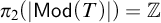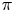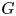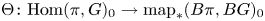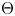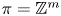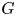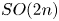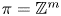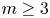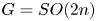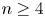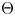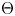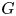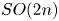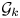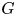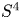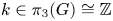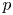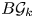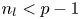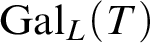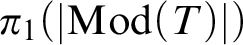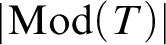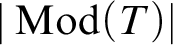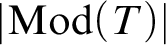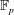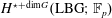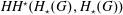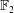Refine search
Actions for selected content:
16 results
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 2224-2239
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFECTING GROUP SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 2549-2591
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-TRIVIAL HIGHER HOMOTOPY OF FIRST-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 January 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The space of commuting elements in a Lie group and maps between classifying spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 735-755
- Print publication:
- June 2025
-
- Article
- Export citation
The mod-p homology of the classifying spaces of certain gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1805-1817
- Print publication:
- December 2023
-
- Article
- Export citation
CLASSIFYING SPACES AND THE LASCAR GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1396-1431
- Print publication:
- December 2021
-
- Article
- Export citation
The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 843-889
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
On the Cohomology of Classifying Spaces of Groups of Homeomorphisms
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 3 / October 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 763-778
-
- Article
-
- You have access
- Export citation
Spaces with Noetherian cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 13-25
-
- Article
-
- You have access
- Export citation
Homology of some Artin and twisted Artin Groups
-
- Journal:
- Journal of K-Theory / Volume 6 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2009, pp. 171-196
- Print publication:
- August 2010
-
- Article
- Export citation
Subgroup families controlling p-local finite groups
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 2 / September 2005
- Published online by Cambridge University Press:
- 23 August 2005, pp. 325-354
- Print publication:
- September 2005
-
- Article
- Export citation
Classifying Spaces for Monoidal Categories Through Geometric Nerves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-331
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
INTERNAL q-HOMOLOGY OF CROSSED MODULES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2004, pp. 397-409
-
- Article
-
- You have access
- Export citation
Classifying Spaces and Boundaries for Relatively Hyperbolic Groups
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 86 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 666-684
- Print publication:
- May 2003
-
- Article
- Export citation
Classifying spaces for polarized mixed Hodge structures and for Brieskorn lattices
-
- Journal:
- Compositio Mathematica / Volume 116 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-37
- Print publication:
- March 1999
-
- Article
-
- You have access
- Export citation
The Topology of Quasibundles
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 6 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1290-1316
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation