We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider the following self-organizing rule called POS(i): after a book in the jth position of a shelf is borrowed, it is moved up one position if j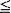
i, and is moved to the ith position if j > i. This is a family of move-forward rules, with POS(l) being the move-to-front rule and POS(n − 1) being the transposition rule where n is the number of books to be organized. We derive explicitly the stationary distribution under the POS(i) rule and show that its search cost compares favorably with that of move-to-front rule under any book access probabilities p1, p1, ···, pn.
