Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T17:48:26.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Cost comparison of a spectrum of self-organizing rules

Part of: Markov processes Theory of data

Published online by Cambridge University Press:  14 July 2016

K. S. Chong  and
K. Lam
K. S. Chong*
Affiliation:
The University of Hong Kong
K. Lam*
Affiliation:
The University of Hong Kong
*
∗Postal address: Statistics Department, The University of Hong Kong, Hong Kong.
∗Postal address: Statistics Department, The University of Hong Kong, Hong Kong.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the following self-organizing rule called POS(i): after a book in the jth position of a shelf is borrowed, it is moved up one position if j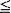i, and is moved to the ith position if j > i. This is a family of move-forward rules, with POS(l) being the move-to-front rule and POS(n − 1) being the transposition rule where n is the number of books to be organized. We derive explicitly the stationary distribution under the POS(i) rule and show that its search cost compares favorably with that of move-to-front rule under any book access probabilities p1, p1, ···, pn.

Keywords

MARKOV CHAIN MODELSLINEAR SEARCHCOMPARISON OF SEARCH COSTSMOVE-FORWARDMOVE-TO-FRONT RULETRANSPOSITION RULESTATIONARY PROBABILITY

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 68P10: Searching and sorting
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 3 , September 1997 , pp. 583 - 592
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of K. Lam is partially supported by a research grant from the University of Hong Kong.

References

Anderson, E. J., Nash, P. and Weber, R. R. (1982) A counterexample to a conjecture on optimal list ordering. J. Appl. Prob. 19, 730–732.CrossRefGoogle Scholar
Bitner, J. R. (1979) Heuristics that dynamically organize data structures. SIAM J. Comput. 8, 82–110.Google Scholar
Hendricks, W. J. (1976) An account of self-organizing systems. SIAM J. Comput. 5, 715–723.CrossRefGoogle Scholar
Kan, Y. C. and Ross, S. M. (1980) Optimal list order under partial memory constraints. J. Appl. Prob. 17, 1004–1015.Google Scholar
Lam, K. (1984) Comparison of self-organizing linear search rules. J. Appl. Prob. 21, 763–776.Google Scholar
Lam, K. and Cowan, R. (1992) Stochastic reversibility in self-organizing systems. Commun. Statist.-Stoch Models 8, 325–336.Google Scholar
Lam, K., Leung, M. Y. and Siu, M. K. (1984) Self-organizing files with dependent accesses. J. Appl. Prob. 21, 343–359.CrossRefGoogle Scholar
Lam, K., Siu, M. K. and Yu, C. T. (1981) A generalized counter scheme. Theoret. Comput. Sci. 16, 271–278.CrossRefGoogle Scholar
Nelson, P. R. (1982) The transposition replacement policy with a partial memory. J. Appl. Prob. 19, 733–736.CrossRefGoogle Scholar
Phatarfod, R. M. (1994) On the transition probabilities of the move-to-front scheme. J. Appl. Prob. 31, 570–574.CrossRefGoogle Scholar
Rivest, R. (1976) On self-organizing sequential search heuristics. Commun. ACM 19, 63–67.Google Scholar
Tenenbaum, A. M. and Nemes, R. M. (1982) Two spectra of self-organizing sequential search algorithms. SIAM J. Comput. 11, 557–566.CrossRefGoogle Scholar