We study the geometry of Hilbert spaces with complete Pick kernels and the geometry of sets in complex hyperbolic space, taking advantage of the correspondence between the two topics. We focus on questions of assembling Hilbert spaces into larger spaces and of assembling sets into larger sets. Model questions include describing the possible three-dimensional subspaces of four-dimensional Hilbert spaces with Pick kernels and describing the possible triangular faces of a tetrahedron in 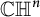 $\mathbb {CH}^{n}$. A novel technical tool is a complex analog of the cosine of a vertex angle.
$\mathbb {CH}^{n}$. A novel technical tool is a complex analog of the cosine of a vertex angle.
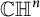 $\mathbb {CH} ^{n}$
$\mathbb {CH} ^{n}$