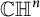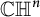1 Introduction and summary
We begin with an informal overview; precise statements are in the later sections.
1.1 Prelude
There are close relationships between the analytic properties of certain Hilbert spaces and the geometric properties of certain sets in complex hyperbolic space. Here, we explore some aspects of those relationships in detail; other aspects are studied in [Reference Arcozzi, Rochberg, Sawyer and WickARSW, Reference RochbergRo, Reference RochbergRo2, Reference RochbergRo3].
1.2 Introduction
A finite-dimensional reproducing kernel Hilbert space (RKHS) may have, or may fail to have, the complete Pick property (CPP), and substantial work has been done establishing which spaces have this property and describing its consequences, for instance, [Reference Agler and PickAM, Reference Arcozzi, Rochberg, Sawyer and WickARSW2, Reference HartzHa, Reference Shalit and AlpaySh]. Here, we study the rules governing building an RKHS+CPP from given pieces using specified amalgamation rules. Because of the correspondence between those Hilbert spaces and finite sets in complex hyperbolic space
![]() $\mathbb {CH}^{n}$
, we obtain at the same time rules governing assembly of finite sets in
$\mathbb {CH}^{n}$
, we obtain at the same time rules governing assembly of finite sets in
![]() $\mathbb {CH}^{n}$
into larger sets.
$\mathbb {CH}^{n}$
into larger sets.
We have two essentially equivalent model questions: one geometric and the other functional analytic. The geometric version of question is more intuitive so we present it first.
Question 1: Given four triangles in complex hyperbolic space,
![]() $\mathbb {CH}^{n},$
is there a tetrahedron in
$\mathbb {CH}^{n},$
is there a tetrahedron in
![]() $\mathbb {CH}^{n}$
with faces congruent to those triangles?
$\mathbb {CH}^{n}$
with faces congruent to those triangles?
In Euclidean space of any dimension, the necessary and sufficient condition for three segments to be the sides of a triangle is that the lengths satisfy the triangle inequality and if that holds then those lengths determine the triangle up to congruence. On the other hand, given four Euclidean triangles with matching side lengths, there might not be a tetrahedron with faces congruent to those triangles, or, what is the same thing, edges the same lengths as the sides of those triangles. For instance, the numbers
![]() $\left \{ 4,4,4,4,4,7\right \} $
are not the edge lengths of a tetrahedron. A necessary and sufficient condition for there to be such a tetrahedron is the nonnegativity of the determinant of the associated Cayley–Menger matrix, a matrix with entries constructed using the side lengths. This is an elegant condition, but it is an inequality for a sixth degree polynomial in the lengths, [Reference Wirth and DreidingWD].
$\left \{ 4,4,4,4,4,7\right \} $
are not the edge lengths of a tetrahedron. A necessary and sufficient condition for there to be such a tetrahedron is the nonnegativity of the determinant of the associated Cayley–Menger matrix, a matrix with entries constructed using the side lengths. This is an elegant condition, but it is an inequality for a sixth degree polynomial in the lengths, [Reference Wirth and DreidingWD].
In real or complex hyperbolic space, the necessary and sufficient condition for three lengths to be the side lengths of a triangle is that they satisfy the hyperbolic version of the triangle inequality (2.2) [Reference RochbergRo]. In
![]() $\mathbb {CH}^{1}$
and in
$\mathbb {CH}^{1}$
and in
![]() $\mathbb {RH}^{n}$
,
$\mathbb {RH}^{n}$
,
![]() $n\geq 1,$
those lengths determine the congruence class of the triangle; but in
$n\geq 1,$
those lengths determine the congruence class of the triangle; but in
![]() $\mathbb {CH}^{n}$
,
$\mathbb {CH}^{n}$
,
![]() $n>1,$
the side lengths do not determine the congruence class and an additional number is needed, for instance, the symplectic area of the triangle. Brehm [Reference BrehmBr] presents the inequalities the four numbers must satisfy and shows that if they are satisfied, then there is a triangle in
$n>1,$
the side lengths do not determine the congruence class and an additional number is needed, for instance, the symplectic area of the triangle. Brehm [Reference BrehmBr] presents the inequalities the four numbers must satisfy and shows that if they are satisfied, then there is a triangle in
![]() $\mathbb {CH}^{n},$
unique up to congruence, with that geometric data. We recall the details in Theorem 3.1.
$\mathbb {CH}^{n},$
unique up to congruence, with that geometric data. We recall the details in Theorem 3.1.
If we are given four triangles to be the faces of a tetrahedron in
![]() $\mathbb {CH}^{n}$
, then the starting data are determined by
$\mathbb {CH}^{n}$
, then the starting data are determined by
![]() $4\times 4=16$
parameters. If it is possible to form the tetrahedron, then various side lengths must be equal, reducing the number of parameters to
$4\times 4=16$
parameters. If it is possible to form the tetrahedron, then various side lengths must be equal, reducing the number of parameters to
![]() $10.$
Further, it is not hard to show that if there is a tetrahedron, then the sum of the signed symplectic areas of the triangular faces must vanish, reducing the number of free parameters to 9. We see in Theorem 3.2 that the congruence class of a tetrahedron in
$10.$
Further, it is not hard to show that if there is a tetrahedron, then the sum of the signed symplectic areas of the triangular faces must vanish, reducing the number of free parameters to 9. We see in Theorem 3.2 that the congruence class of a tetrahedron in
![]() $\mathbb {CH}^{n}$
is determined by nine numbers; Question 1 asks for the constraints those numbers must satisfy, and in Section 6, we give the explicit inequalities.
$\mathbb {CH}^{n}$
is determined by nine numbers; Question 1 asks for the constraints those numbers must satisfy, and in Section 6, we give the explicit inequalities.
The relative complexity of the results for Euclidean space in [Reference Wirth and DreidingWD] is partially due to the choice of side lengths as data. In answering Question 1, in addition to working with side lengths, we also consider the geometry of the vertices. We describe them using a functional
![]() $\operatorname *{kos}_{a}(b,c)$
of triples of points
$\operatorname *{kos}_{a}(b,c)$
of triples of points
![]() $\left \{ a,b,c\right \} $
in
$\left \{ a,b,c\right \} $
in
![]() $\mathbb {CH}^{n}$
which is a complex analog of the cosine of the angle at the vertex a formed by the segments
$\mathbb {CH}^{n}$
which is a complex analog of the cosine of the angle at the vertex a formed by the segments
![]() $ab$
and
$ab$
and
![]() $ac.$
If we can form a tetrahedron from given triangles, then at a vertex a of the tetrahedron there will be three edges and three bivalent vertices. The shape of each bivalent vertex is determined by a value of
$ac.$
If we can form a tetrahedron from given triangles, then at a vertex a of the tetrahedron there will be three edges and three bivalent vertices. The shape of each bivalent vertex is determined by a value of
![]() $\operatorname *{kos}_{a}(\cdot ,\cdot )$
. The lengths of those three edges together with the three complex values of
$\operatorname *{kos}_{a}(\cdot ,\cdot )$
. The lengths of those three edges together with the three complex values of
![]() $\operatorname *{kos}$
for the bivalent vertices give nine real parameters which suffice to determine if there is a tetrahedron and if so to determine its congruence class.
$\operatorname *{kos}$
for the bivalent vertices give nine real parameters which suffice to determine if there is a tetrahedron and if so to determine its congruence class.
Here is an informal statement of our results on Question 1. The first part is a restatement of Brehm’s result, and the second part is from Theorem 6.2. It includes the algebraic inequality that the values
![]() $\operatorname *{kos} _{a}(\cdot ,\cdot )$
must satisfy for there to be a tetrahedron.
$\operatorname *{kos} _{a}(\cdot ,\cdot )$
must satisfy for there to be a tetrahedron.
Theorem 1.1
-
(1) If
 $a,x,y$
are vertices of a triangle in
$a,x,y$
are vertices of a triangle in
 $\mathbb {CH}^{n}$
, then the two real numbers
$\mathbb {CH}^{n}$
, then the two real numbers
 $\operatorname *{length}\left ( ax\right ) $
and
$\operatorname *{length}\left ( ax\right ) $
and
 $\operatorname *{length}(ay)$
together with the complex number
$\operatorname *{length}(ay)$
together with the complex number
 $\operatorname *{kos}_{a}(x,y)$
determine the congruence class of the triangle.
$\operatorname *{kos}_{a}(x,y)$
determine the congruence class of the triangle.The lengths must be in the interval
 $(0,1)$
, and we must have
$(0,1)$
, and we must have
 $\left \vert \operatorname *{kos}_{a}(x,y)\right \vert \leq 1$
. Given data that satisfy those conditions, there is a triangle with those data.
$\left \vert \operatorname *{kos}_{a}(x,y)\right \vert \leq 1$
. Given data that satisfy those conditions, there is a triangle with those data. -
(2) If
 $a,x,y,z$
are the vertices of a tetrahedron
$a,x,y,z$
are the vertices of a tetrahedron
 $\mathbb {CH}^{n}$
, then the three real numbers
$\mathbb {CH}^{n}$
, then the three real numbers
 $\operatorname *{length}\left ( ax\right ) ,$
$\operatorname *{length}\left ( ax\right ) ,$
 $\operatorname *{length}(ay)$
, and
$\operatorname *{length}(ay)$
, and
 $\operatorname *{length}\left ( az\right ) $
together with the three complex numbers
$\operatorname *{length}\left ( az\right ) $
together with the three complex numbers
 $\operatorname *{kos}\nolimits _{a} (y,z)$
,
$\operatorname *{kos}\nolimits _{a} (y,z)$
,
 $\operatorname *{kos}\nolimits _{a}(z,x)$
, and
$\operatorname *{kos}\nolimits _{a}(z,x)$
, and
 $\operatorname *{kos} \nolimits _{a}(x,y)$
determine the congruence class of the tetrahedron.
$\operatorname *{kos} \nolimits _{a}(x,y)$
determine the congruence class of the tetrahedron.The lengths must be in the interval
 $(0,1)$
, and the values of
$(0,1)$
, and the values of
 $\operatorname *{kos}$
must be of modulus at most one and satisfy (1.1)
$\operatorname *{kos}$
must be of modulus at most one and satisfy (1.1) $$ \begin{align} \left\vert \operatorname*{kos}\nolimits_{a}(y,z)-\overline{\operatorname*{kos} \nolimits_{a}(x,y)}\operatorname*{kos}\nolimits_{a}(x,z)\right\vert ^{2} \leq(1-\left\vert \operatorname*{kos}\nolimits_{a}(x,y)\right\vert ^{2})(1-\left\vert \operatorname*{kos}\nolimits_{a}(x,z)\right\vert ^{2}). \end{align} $$
$$ \begin{align} \left\vert \operatorname*{kos}\nolimits_{a}(y,z)-\overline{\operatorname*{kos} \nolimits_{a}(x,y)}\operatorname*{kos}\nolimits_{a}(x,z)\right\vert ^{2} \leq(1-\left\vert \operatorname*{kos}\nolimits_{a}(x,y)\right\vert ^{2})(1-\left\vert \operatorname*{kos}\nolimits_{a}(x,z)\right\vert ^{2}). \end{align} $$
Given data that satisfy those inequalities, there is a tetrahedron with those data.
The functional
![]() $\operatorname *{kos}$
and also the functional
$\operatorname *{kos}$
and also the functional
![]() $\delta (\cdot ,\cdot ),$
the pseudohyperbolic distance between pairs of points, are defined for points in
$\delta (\cdot ,\cdot ),$
the pseudohyperbolic distance between pairs of points, are defined for points in
![]() $\mathbb {CH}^{n}$
. The “same” functionals are also defined for tuples of kernel functions in any RKHS. In an RKHS,
$\mathbb {CH}^{n}$
. The “same” functionals are also defined for tuples of kernel functions in any RKHS. In an RKHS,
![]() $\delta (a,b)$
is related to the angle between kernel functions and
$\delta (a,b)$
is related to the angle between kernel functions and
![]() $\operatorname *{kos} _{a}(b,c)$
describes the geometry of the projection of one kernel function onto the linear span two others. The functionals defined on points in
$\operatorname *{kos} _{a}(b,c)$
describes the geometry of the projection of one kernel function onto the linear span two others. The functionals defined on points in
![]() $\mathbb {CH}^{n}$
are invariant under automorphisms of
$\mathbb {CH}^{n}$
are invariant under automorphisms of
![]() $\mathbb {CH}^{n},$
and the RKHS versions are invariant under rescalings of the Hilbert space. Accepting the guidance of Klein’s Erlangen Program, these invariant quantities are geometric descriptors of sets in
$\mathbb {CH}^{n},$
and the RKHS versions are invariant under rescalings of the Hilbert space. Accepting the guidance of Klein’s Erlangen Program, these invariant quantities are geometric descriptors of sets in
![]() $\mathbb {CH}^{n}$
and of RKHS.
$\mathbb {CH}^{n}$
and of RKHS.
In Theorem 5.1, we use those functionals to give similar descriptions of finite sets in
![]() $\mathbb {CH}^{n}$
and of finite-dimensional RKHS with the CPP. The similarity extends to assembly questions in the two contexts, and in particular, Question 1 is essentially equivalent to the following.
$\mathbb {CH}^{n}$
and of finite-dimensional RKHS with the CPP. The similarity extends to assembly questions in the two contexts, and in particular, Question 1 is essentially equivalent to the following.
Question 2: Given four three-dimensional RKHS+CPP, is there a four-dimensional space RKHS+CPP whose regular three-dimensional subspaces are rescalings of the given spaces?
A basic question is giving conditions which insure a finite-dimensional RKHS H has the CPP. The question is trivial if H is one-dimensional and elementary if the dimension is 2. Because having the CPP is equivalent to an associated geometric configuration being realizable in
![]() $\mathbb {CH}^{n}$
, the three-dimensional case is settled by Brehm’s result, the first statement in the previous theorem. If H is four-dimensional, then it is certainly necessary that each regular three-dimensional subspace satisfies Brehm’s condition, but an example due to Quiggin [Reference Raghupathi and PaulsenQ] shows that those conditions are not sufficient. This work arose as an attempt to place Quiggin’s example in a general context and gives necessary and sufficient conditions for questions such as Question 2 to have a positive answer. The specific answer to Question 2, given in Theorem 6.4, is an inequality for values of the functional
$\mathbb {CH}^{n}$
, the three-dimensional case is settled by Brehm’s result, the first statement in the previous theorem. If H is four-dimensional, then it is certainly necessary that each regular three-dimensional subspace satisfies Brehm’s condition, but an example due to Quiggin [Reference Raghupathi and PaulsenQ] shows that those conditions are not sufficient. This work arose as an attempt to place Quiggin’s example in a general context and gives necessary and sufficient conditions for questions such as Question 2 to have a positive answer. The specific answer to Question 2, given in Theorem 6.4, is an inequality for values of the functional
![]() $\operatorname *{kos}.$
$\operatorname *{kos}.$
A theme of this paper is that certain geometric questions such as Question 1 and Hilbert space questions such as Question 2 are equivalent. Although we could have given a geometric analysis of Question 1 or a Hilbert space analysis of Question 2, we have combined the two viewpoints to emphasize their unity. However, the geometric language often seems to carry more intuition, for instance, discussing congruence of sets rather than rescaling of Hilbert spaces, and so we often just use the geometric language and do not record the equivalent Hilbert space statements. However, the Hilbert space statements are always part of the story and, in fact, it is the author’s view that they are more fundamental.
1.3 Contents
Here is an overview of the contents. In the next section, we give background information about geometry and about Hilbert spaces; in the section after that, we recall results connecting those topics. In Section 3, we formulate our basic assembly and coherence question and explain why Questions 1 and 2 are equivalent. Most of our analysis is based on the functional
![]() $\operatorname *{kos}$
introduced in Section 2. That functional is new, and we take time in Section 4 to discuss the geometry associated with it. In Section 5, we describe finite sets X in
$\operatorname *{kos}$
introduced in Section 2. That functional is new, and we take time in Section 4 to discuss the geometry associated with it. In Section 5, we describe finite sets X in
![]() $\mathbb {CH}^{n},$
and also an associated class of Hilbert spaces H. We use a version of spherical coordinates with values of
$\mathbb {CH}^{n},$
and also an associated class of Hilbert spaces H. We use a version of spherical coordinates with values of
![]() $\operatorname *{kos}$
taking the role of cosines of angles. That description involves the positive semidefiniteness of a matrix
$\operatorname *{kos}$
taking the role of cosines of angles. That description involves the positive semidefiniteness of a matrix
![]() $A,$
$A,$
![]() $A\succcurlyeq 0,$
which has the form
$A\succcurlyeq 0,$
which has the form
![]() $A= \left ( \operatorname *{kos} _{1}(i,j)\right ) .$
Principal submatrices of A encode the geometry of subsets of X and of subspaces of
$A= \left ( \operatorname *{kos} _{1}(i,j)\right ) .$
Principal submatrices of A encode the geometry of subsets of X and of subspaces of
![]() $H,$
and Sylvester’s criterion lets us recast the fact that
$H,$
and Sylvester’s criterion lets us recast the fact that
![]() $A\succcurlyeq 0$
as statements about those submatrices. We use that to relate the geometry of X to the geometry of its subsets and the geometry of H to that of its subspaces. In Section 6, we specialize the results from Section 5 to four-point sets and four-dimensional spaces, answer Questions 1 and 2, and analyze the examples of Quiggin [Reference Raghupathi and PaulsenQ].
$A\succcurlyeq 0$
as statements about those submatrices. We use that to relate the geometry of X to the geometry of its subsets and the geometry of H to that of its subspaces. In Section 6, we specialize the results from Section 5 to four-point sets and four-dimensional spaces, answer Questions 1 and 2, and analyze the examples of Quiggin [Reference Raghupathi and PaulsenQ].
In Section 6.4, we consider what happens when a four-point set in
![]() $\mathbb {CH}^{n}$
is in fact inside a copy of
$\mathbb {CH}^{n}$
is in fact inside a copy of
![]() $\mathbb {RH}^{k}$
. Then our results specialize to results about sets in real hyperbolic space and there is then a fundamental simplification, the value of
$\mathbb {RH}^{k}$
. Then our results specialize to results about sets in real hyperbolic space and there is then a fundamental simplification, the value of
![]() $\operatorname *{kos}$
at a vertex equals the cosine of the vertex angle. The earlier results then simplify to the classical constraints on the vertex angles or the dihedral angles of a tetrahedron in real hyperbolic space or Euclidean space.
$\operatorname *{kos}$
at a vertex equals the cosine of the vertex angle. The earlier results then simplify to the classical constraints on the vertex angles or the dihedral angles of a tetrahedron in real hyperbolic space or Euclidean space.
The brief final section contains a few remarks.
2 Background
2.1 Hyperbolic geometry
A background reference for complex hyperbolic geometry is [Reference GoldmanGo]. We will use the ball model of complex hyperbolic space
![]() $\mathbb {CH}^{n}.$
In that model, the manifold for
$\mathbb {CH}^{n}.$
In that model, the manifold for
![]() $\mathbb {CH}^{n}$
is the unit ball,
$\mathbb {CH}^{n}$
is the unit ball,
![]() $\mathbb {B} _{n}\subset \mathbb {C}^{n},$
and the geometry is the Poincare Bergman geometry determined by the transitive group of biholomorphic automorphisms of the ball,
$\mathbb {B} _{n}\subset \mathbb {C}^{n},$
and the geometry is the Poincare Bergman geometry determined by the transitive group of biholomorphic automorphisms of the ball,
![]() $\operatorname *{Aut}\mathbb {B}_{n}$
. For each
$\operatorname *{Aut}\mathbb {B}_{n}$
. For each
![]() $\alpha \in \mathbb {B}_{n}$
, there is a unique involution
$\alpha \in \mathbb {B}_{n}$
, there is a unique involution
![]() $\phi _{a}\in \operatorname *{Aut}\mathbb {B}_{n}$
, which satisfies
$\phi _{a}\in \operatorname *{Aut}\mathbb {B}_{n}$
, which satisfies
![]() $\phi _{a}(a)=0.$
The group
$\phi _{a}(a)=0.$
The group
![]() $\operatorname *{Aut}\mathbb {B}_{n}$
is generated by those involutions together with the unitary maps. We will say two sets Z,
$\operatorname *{Aut}\mathbb {B}_{n}$
is generated by those involutions together with the unitary maps. We will say two sets Z,
![]() $W\subset \mathbb {CH}^{n}$
are congruent,
$W\subset \mathbb {CH}^{n}$
are congruent,
![]() $Z\sim W,$
if there is a
$Z\sim W,$
if there is a
![]() $\phi \in \operatorname *{Aut}\mathbb {B}_{n}$
with
$\phi \in \operatorname *{Aut}\mathbb {B}_{n}$
with
![]() $\phi (Z)=W.$
If the sets are ordered then, absent other comment, we suppose that
$\phi (Z)=W.$
If the sets are ordered then, absent other comment, we suppose that
![]() $\phi $
respects the ordering. Congruence is an equivalence relation, and we are particularly interested in congruence equivalence classes.
$\phi $
respects the ordering. Congruence is an equivalence relation, and we are particularly interested in congruence equivalence classes.
The pseudohyperbolic metric
![]() $\delta $
on
$\delta $
on
![]() $\mathbb {CH}^{n}$
is defined by
$\mathbb {CH}^{n}$
is defined by
![]() $\forall \alpha ,\beta \in \mathbb {CH}^{n}$
$\forall \alpha ,\beta \in \mathbb {CH}^{n}$
Equivalently,
![]() $\delta $
is the distance on
$\delta $
is the distance on
![]() $\mathbb {B}_{n}$
, which satisfies
$\mathbb {B}_{n}$
, which satisfies
![]() $\delta (0,z)=\left \vert z\right \vert $
for
$\delta (0,z)=\left \vert z\right \vert $
for
![]() $z\in \mathbb {B}_{n}$
and is
$z\in \mathbb {B}_{n}$
and is
![]() $\operatorname *{Aut}\mathbb {B}_{n}$
invariant [Reference Duren and WeirDW].
$\operatorname *{Aut}\mathbb {B}_{n}$
invariant [Reference Duren and WeirDW].
![]() $\delta $
is not a length metric; the length metric it generates is the Poincare Bergman metric for the ball normalized to agree with the Euclidean metric to second order at the origin. For
$\delta $
is not a length metric; the length metric it generates is the Poincare Bergman metric for the ball normalized to agree with the Euclidean metric to second order at the origin. For
![]() $n=1$
, the formula is
$n=1$
, the formula is
![]() $\delta (\alpha ,\beta )=\left \vert \frac {\alpha -\beta }{1-\bar {\beta }\alpha }\right \vert .$
The formula for general n is given in (2.9).
$\delta (\alpha ,\beta )=\left \vert \frac {\alpha -\beta }{1-\bar {\beta }\alpha }\right \vert .$
The formula for general n is given in (2.9).
![]() $\delta $
satisfies a strengthened version of the triangle inequality, [Reference Duren and WeirDW]; for
$\delta $
satisfies a strengthened version of the triangle inequality, [Reference Duren and WeirDW]; for
![]() $x,y,z\in \mathbb {B}_{n}$
,
$x,y,z\in \mathbb {B}_{n}$
,
 $$ \begin{align} \frac{\left\vert \delta(x,z)-\delta(z,y)\right\vert }{1-\delta(x,z)\delta (z,y)}\leq\delta(x,y)\leq\frac{\delta(x,z)+\delta(z,y)}{1+\delta (x,z)\delta(z,y)}. \end{align} $$
$$ \begin{align} \frac{\left\vert \delta(x,z)-\delta(z,y)\right\vert }{1-\delta(x,z)\delta (z,y)}\leq\delta(x,y)\leq\frac{\delta(x,z)+\delta(z,y)}{1+\delta (x,z)\delta(z,y)}. \end{align} $$
The space
![]() $\mathbb {CH}^{n}$
contains various totally geodesic submanifolds of interest here. These include the classical geodesics which are totally geodesic copies of
$\mathbb {CH}^{n}$
contains various totally geodesic submanifolds of interest here. These include the classical geodesics which are totally geodesic copies of
![]() $\mathbb {RH}^{1},$
and also include totally geodesic copies of
$\mathbb {RH}^{1},$
and also include totally geodesic copies of
![]() $\mathbb {CH}^{1},$
sometimes called complex geodesics. Every pair of points is contained in a unique classical geodesic which is in turn contained in a unique complex geodesic. There are also totally geodesic copies of the real hyperbolic plane
$\mathbb {CH}^{1},$
sometimes called complex geodesics. Every pair of points is contained in a unique classical geodesic which is in turn contained in a unique complex geodesic. There are also totally geodesic copies of the real hyperbolic plane
![]() $\mathbb {RH}^{2}$
inside
$\mathbb {RH}^{2}$
inside
![]() $\mathbb {CH} ^{n}.$
In particular, for
$\mathbb {CH} ^{n}.$
In particular, for
![]() ${\mathbb {R}^{2}=\left \{ \left ( x,y,0,...,0\right ) :x,y\in \mathbb {R}\right \} \subset \mathbb {C}^{n}}$
, consider the two-dimensional real ball,
${\mathbb {R}^{2}=\left \{ \left ( x,y,0,...,0\right ) :x,y\in \mathbb {R}\right \} \subset \mathbb {C}^{n}}$
, consider the two-dimensional real ball,
![]() $RB_{2}=\mathbb {R}^{2}\cap \mathbb {CH}^{n}.$
That intersection is a totally geodesically embedded submanifold whose induced geometry is that of the Beltrami–Klein model of
$RB_{2}=\mathbb {R}^{2}\cap \mathbb {CH}^{n}.$
That intersection is a totally geodesically embedded submanifold whose induced geometry is that of the Beltrami–Klein model of
![]() $\mathbb {RH}^{2}$
with constant curvature
$\mathbb {RH}^{2}$
with constant curvature
![]() $-1/4.$
All of the automorphic images of
$-1/4.$
All of the automorphic images of
![]() $RB_{2}$
are also totally geodesically embedded submanifolds of real dimension 2, and they, together with the complex geodesics, are the only such.
$RB_{2}$
are also totally geodesically embedded submanifolds of real dimension 2, and they, together with the complex geodesics, are the only such.
The geometry of
![]() $RB_{2}$
is not conformal with the Euclidean geometry of the containing
$RB_{2}$
is not conformal with the Euclidean geometry of the containing
![]() $\mathbb {R}^{2}.$
However, the two geometries are conformally equivalent at the origin, in particular angles with vertex at the origin have the same size in both geometries. There is a useful picture of
$\mathbb {R}^{2}.$
However, the two geometries are conformally equivalent at the origin, in particular angles with vertex at the origin have the same size in both geometries. There is a useful picture of
![]() $RB_{2}$
in [Reference GoldmanGo, p. 83], and there is a discussion of the geometry of that model (although the version with curvature
$RB_{2}$
in [Reference GoldmanGo, p. 83], and there is a discussion of the geometry of that model (although the version with curvature
![]() $-1)$
as well as the more familiar Poincaré disk model in Appendices B and C of [Reference JansonJ].
$-1)$
as well as the more familiar Poincaré disk model in Appendices B and C of [Reference JansonJ].
If G is a complex geodesic and
![]() $x\in \mathbb {CH}^{n}$
, we define the metric projection of x onto G,
$x\in \mathbb {CH}^{n}$
, we define the metric projection of x onto G,
![]() $P_{G}x,$
to be that point in G which is closest to x in the pseudohyperbolic metric.
$P_{G}x,$
to be that point in G which is closest to x in the pseudohyperbolic metric.
For
![]() $z,w\in \mathbb {B}_{r}$
, we define the kernel function k by
$z,w\in \mathbb {B}_{r}$
, we define the kernel function k by
(We write
![]() $\left \langle \left \langle \cdot ,\cdot \right \rangle \right \rangle $
for the inner product on
$\left \langle \left \langle \cdot ,\cdot \right \rangle \right \rangle $
for the inner product on
![]() $\mathbb {C}^{n}$
to distinguish from the inner products on the general Hilbert spaces we consider.)
$\mathbb {C}^{n}$
to distinguish from the inner products on the general Hilbert spaces we consider.)
There is a fundamental identity which describes the interaction of the involutive automorphisms with the kernel functions [Reference RudinRu]: for any
![]() $y,z,w\in \mathbb {B}_{r}$
,
$y,z,w\in \mathbb {B}_{r}$
,
 $$ \begin{align} k(\phi_{y}(z),\phi_{y}(w))=\frac{k\left( y,y\right) ^{1/2}}{k(z,y)} \frac{k\left( y,y\right) ^{1/2}}{k(y,w)}k(z,w). \end{align} $$
$$ \begin{align} k(\phi_{y}(z),\phi_{y}(w))=\frac{k\left( y,y\right) ^{1/2}}{k(z,y)} \frac{k\left( y,y\right) ^{1/2}}{k(y,w)}k(z,w). \end{align} $$
By a triangle in
![]() $\mathbb {CH}^{n}$
, we mean an ordered set of three distinct points called vertices, or those vertices together with the sides, the geodesic segments connecting the vertices. We allow the degenerate case of three points in a single geodesic. The length of a side is the
$\mathbb {CH}^{n}$
, we mean an ordered set of three distinct points called vertices, or those vertices together with the sides, the geodesic segments connecting the vertices. We allow the degenerate case of three points in a single geodesic. The length of a side is the
![]() $\delta $
distance between the corresponding vertices. Triangles in
$\delta $
distance between the corresponding vertices. Triangles in
![]() $\mathbb {CH}^{n}$
do not necessarily have “faces”; three points in
$\mathbb {CH}^{n}$
do not necessarily have “faces”; three points in
![]() $\mathbb {CH}^{n}$
are not generally contained in a totally geodesic submanifold of real dimension 2.
$\mathbb {CH}^{n}$
are not generally contained in a totally geodesic submanifold of real dimension 2.
Similarly, a tetrahedron in
![]() $\mathbb {CH}^{n}$
is an ordered set of four vertices. Its four subsets of three vertices are its triangular faces, even though they may not be faces in the geometric sense.
$\mathbb {CH}^{n}$
is an ordered set of four vertices. Its four subsets of three vertices are its triangular faces, even though they may not be faces in the geometric sense.
2.2 Hilbert spaces with reproducing kernels
Our background references for Hilbert spaces are [Reference Agler and PickAM, Reference Arcozzi, Rochberg, Sawyer and WickARSW2, Reference QuigginPR, Reference RochbergRo].
Except for the spaces
![]() $DA_{r}$
discussed this section, all the Hilbert spaces in this paper are finite-dimensional.
$DA_{r}$
discussed this section, all the Hilbert spaces in this paper are finite-dimensional.
An n-dimensional RKHS is an n-dimensional Hilbert space H together with a distinguished basis of vectors called reproducing kernels,
![]() $RK(H)=\left \{ h_{i}\right \} _{i=1}^{n}.$
For any
$RK(H)=\left \{ h_{i}\right \} _{i=1}^{n}.$
For any
![]() $v\in H$
, we write
$v\in H$
, we write
![]() $\hat {v}$
for its normalized version;
$\hat {v}$
for its normalized version;
![]() $\hat {v}=v/\left \Vert v\right \Vert .$
For
$\hat {v}=v/\left \Vert v\right \Vert .$
For
![]() $h_{i},h_{j}\in RK(H)$
, we write
$h_{i},h_{j}\in RK(H)$
, we write
![]() $h_{ij}$
for their inner product and
$h_{ij}$
for their inner product and
![]() $\widehat {h_{ij}}$
for the inner product of their normalizations:
$\widehat {h_{ij}}$
for the inner product of their normalizations:
 $$\begin{align*}h_{ij}=\left\langle h_{i},h_{j}\right\rangle ,\ \ \ \widehat{h_{ij} }=\left\langle \widehat{h_{i}},\widehat{h_{j}}\right\rangle =\left\langle \frac{h_{i}}{\left\Vert h_{i}\right\Vert },\frac{h_{j}}{\left\Vert h_{j}\right\Vert }\right\rangle. \end{align*}$$
$$\begin{align*}h_{ij}=\left\langle h_{i},h_{j}\right\rangle ,\ \ \ \widehat{h_{ij} }=\left\langle \widehat{h_{i}},\widehat{h_{j}}\right\rangle =\left\langle \frac{h_{i}}{\left\Vert h_{i}\right\Vert },\frac{h_{j}}{\left\Vert h_{j}\right\Vert }\right\rangle. \end{align*}$$
The Gram matrix of H is the matrix
![]() $\operatorname *{Gr}(H)=\left ( h_{ij}\right ) _{i,j=1}^{n}.$
$\operatorname *{Gr}(H)=\left ( h_{ij}\right ) _{i,j=1}^{n}.$
Any v in H is regarded as a function on the index set of
![]() $RK(H)$
by setting
$RK(H)$
by setting
![]() ${v(i)=\left \langle v,h_{i}\right \rangle} $
. If m is a function on
${v(i)=\left \langle v,h_{i}\right \rangle} $
. If m is a function on
![]() $RK(H)$
, then the associated multiplier operator
$RK(H)$
, then the associated multiplier operator
![]() $M_{m}$
acting on H is the linear operator which satisfies
$M_{m}$
acting on H is the linear operator which satisfies
![]() $M_{m}v(i)=m(i)v(i).$
$M_{m}v(i)=m(i)v(i).$
A regular subspace of H is a subspace J spanned by a subset S of
![]() $RK(H)$
and regarded as an RKHS by setting
$RK(H)$
and regarded as an RKHS by setting
![]() $RK(J)=S.$
$RK(J)=S.$
We now recall the Drury–Arveson spaces,
![]() $DA_{r}$
; some basic references are [Reference Agler and PickAM, Reference ArvesonAr, Reference Shalit and AlpaySh]. With
$DA_{r}$
; some basic references are [Reference Agler and PickAM, Reference ArvesonAr, Reference Shalit and AlpaySh]. With
![]() $k_{z}(\cdot )$
the functions from (2.3),
$k_{z}(\cdot )$
the functions from (2.3),
![]() $DA_{r}$
is the infinite-dimensional RKHS with kernel functions
$DA_{r}$
is the infinite-dimensional RKHS with kernel functions
![]() $\left \{ k_{z}:z\in \mathbb {B}_{r}=\mathbb {CH}^{r}\right \} $
and inner product given by
$\left \{ k_{z}:z\in \mathbb {B}_{r}=\mathbb {CH}^{r}\right \} $
and inner product given by
![]() $\left \langle k_{s},k_{t}\right \rangle =k_{s}(t).$
$\left \langle k_{s},k_{t}\right \rangle =k_{s}(t).$
![]() $DA_{1}$
is the classical Hardy space
$DA_{1}$
is the classical Hardy space
![]() $H^{2}$
of the unit circle, a space which can also be described as the space of holomorphic functions on the unit disk with square summable sequences of Taylor coefficients. For
$H^{2}$
of the unit circle, a space which can also be described as the space of holomorphic functions on the unit disk with square summable sequences of Taylor coefficients. For
![]() $r>1$
,
$r>1$
,
![]() $DA_{r}$
is a proper subspace of the Hardy space of the sphere. It is in the scale of Besov–Sobolev spaces, which also contains the Hardy space of the sphere and the Bergman space of the ball [Reference Arcozzi, Rochberg, Sawyer and WickARSW2].
$DA_{r}$
is a proper subspace of the Hardy space of the sphere. It is in the scale of Besov–Sobolev spaces, which also contains the Hardy space of the sphere and the Bergman space of the ball [Reference Arcozzi, Rochberg, Sawyer and WickARSW2].
We are particularly interested in finite-dimensional regular subspaces of
![]() $DA_{r}$
. For
$DA_{r}$
. For
![]() $Z=\left \{ z_{j}\right \} _{j=1}^{n}\subset \mathbb {CH}^{r}$
, let
$Z=\left \{ z_{j}\right \} _{j=1}^{n}\subset \mathbb {CH}^{r}$
, let
![]() $DA_{r}(Z)$
be the regular subspace of
$DA_{r}(Z)$
be the regular subspace of
![]() $DA_{r}$
spanned by the kernel functions
$DA_{r}$
spanned by the kernel functions
![]() $\left \{ k_{z_{i}}\right \} _{i=1}^{n}.$
We abbreviate them by
$\left \{ k_{z_{i}}\right \} _{i=1}^{n}.$
We abbreviate them by
![]() $\left \{ k_{i}\right \} $
and set
$\left \{ k_{i}\right \} $
and set
![]() $k_{ij}=\left \langle k_{i},k_{j} \right \rangle .$
$k_{ij}=\left \langle k_{i},k_{j} \right \rangle .$
If
![]() $r^{\prime }>r$
, there are natural inclusions of
$r^{\prime }>r$
, there are natural inclusions of
![]() $DA_{r}$
,
$DA_{r}$
,
![]() $\mathbb {C}^{r}$
,
$\mathbb {C}^{r}$
,
![]() $\mathbb {B}_{r}$
, and
$\mathbb {B}_{r}$
, and
![]() $\mathbb {CH}^{r}$
into the corresponding objects with
$\mathbb {CH}^{r}$
into the corresponding objects with
![]() $r^{\prime }.$
These inclusions interact in harmless ways with the constructions we are using. For instance, an inclusion of
$r^{\prime }.$
These inclusions interact in harmless ways with the constructions we are using. For instance, an inclusion of
![]() $\mathbb {B}_{r}$
into
$\mathbb {B}_{r}$
into
![]() $\mathbb {B}_{r^{\prime }}$
takes
$\mathbb {B}_{r^{\prime }}$
takes
![]() $Z\subset \mathbb {B}_{r}$
to a
$Z\subset \mathbb {B}_{r}$
to a
![]() $Z^{\prime }\subset \mathbb {B}_{r^{\prime }}.$
There is then an obvious natural map of
$Z^{\prime }\subset \mathbb {B}_{r^{\prime }}.$
There is then an obvious natural map of
![]() $DA_{r}(Z)$
onto
$DA_{r}(Z)$
onto
![]() $DA_{r^{\prime }}(Z^{\prime })$
which preserves all the structure of interest here. Going forward, we will suppose r is sufficiently large, identify such pairs of sets and spaces, and drop the subscript
$DA_{r^{\prime }}(Z^{\prime })$
which preserves all the structure of interest here. Going forward, we will suppose r is sufficiently large, identify such pairs of sets and spaces, and drop the subscript
![]() $r;$
thus,
$r;$
thus,
![]() $DA(Z).$
$DA(Z).$
2.2.1 Rescaling
Rescaling is a fundamental equivalence relation between RKHSs. Given a finite-dimensional RKHS,
![]() $G,H$
with
$G,H$
with
![]() $RK(H)=\left \{ h_{\alpha }\right \} _{\alpha \in A}$
,
$RK(H)=\left \{ h_{\alpha }\right \} _{\alpha \in A}$
,
![]() $RK(G)=\left \{ g_{\beta }\right \} _{\beta \in B}$
, we say G is a rescaling of H and write
$RK(G)=\left \{ g_{\beta }\right \} _{\beta \in B}$
, we say G is a rescaling of H and write
![]() $G\sim H$
if there is a one-to-one map
$G\sim H$
if there is a one-to-one map
![]() $\theta $
of A onto B and a nonvanishing complex valued function
$\theta $
of A onto B and a nonvanishing complex valued function
![]() $\gamma $
defined on A such that for all
$\gamma $
defined on A such that for all
![]() $\alpha _{1},\alpha _{2}$
in
$\alpha _{1},\alpha _{2}$
in
![]() $A,$
$A,$
For instance, the linear map which sends each kernel function
![]() $h_{\alpha }$
to its normalized version,
$h_{\alpha }$
to its normalized version,
![]() $\widehat {h_{\alpha }}=h_{\alpha }/\left \Vert h_{\alpha }\right \Vert $
is a rescaling. If A and B are ordered, then, unless we specify otherwise, we suppose that
$\widehat {h_{\alpha }}=h_{\alpha }/\left \Vert h_{\alpha }\right \Vert $
is a rescaling. If A and B are ordered, then, unless we specify otherwise, we suppose that
![]() $\theta $
respects the ordering.
$\theta $
respects the ordering.
A basic class of rescalings in our discussion are those induced on spaces
![]() $DA(Z)$
by ball automorphisms. It is a consequence of (2.4) that given any
$DA(Z)$
by ball automorphisms. It is a consequence of (2.4) that given any
![]() $Z\subset \mathbb {B}_{r}$
and any
$Z\subset \mathbb {B}_{r}$
and any
![]() $y\in \mathbb {B}$
, the automorphism
$y\in \mathbb {B}$
, the automorphism
![]() $\phi _{y}$
induces a rescaling of
$\phi _{y}$
induces a rescaling of
![]() $DA(Z)$
to
$DA(Z)$
to
![]() $DA(\phi _{y}(Z)).$
$DA(\phi _{y}(Z)).$
If
![]() $G_{H}$
is a regular subspace of G and
$G_{H}$
is a regular subspace of G and
![]() $H\sim G_{H}$
, we will write
$H\sim G_{H}$
, we will write
![]() $H\leadsto G$
or
$H\leadsto G$
or
![]() $H\leadsto G_{H}\subset G$
and will say that H has a rescaling into
$H\leadsto G_{H}\subset G$
and will say that H has a rescaling into
![]() $G.$
$G.$
2.2.2 Assuming irreducibility
In [Reference Agler and PickAM, p. 79], an RKHS H is called irreducible if no two elements of
![]() $RK(H)$
are parallel and no two are orthogonal. We denote the class of all finite-dimensional irreducible RKHSs by
$RK(H)$
are parallel and no two are orthogonal. We denote the class of all finite-dimensional irreducible RKHSs by
![]() $\mathcal {RK}$
. If
$\mathcal {RK}$
. If
![]() $H\in \mathcal {RK}$
, then the entries of the Gram matrix of H are nonzero. That is convenient when we define the invariants
$H\in \mathcal {RK}$
, then the entries of the Gram matrix of H are nonzero. That is convenient when we define the invariants
![]() $\delta $
and
$\delta $
and
![]() $\operatorname *{kos}$
later.
$\operatorname *{kos}$
later.
The
![]() $DA(X)$
spaces we work with here all irreducible. The first condition is a consequence of their definitions; the second holds because the kernel functions in (2.3) are nonvanishing.
$DA(X)$
spaces we work with here all irreducible. The first condition is a consequence of their definitions; the second holds because the kernel functions in (2.3) are nonvanishing.
2.2.3 The complete Pick property
The CPP is a property which some
![]() $H\in \mathcal {RK}$
have and some do not. The class of H with that property is of fundamental importance in function-theoretic operator theory and is actively studied. Some background references are [Reference Agler and PickAM, Reference ArvesonAr, Reference Arcozzi, Rochberg, Sawyer and WickARSW2, Reference Shalit and AlpaySh]. A sample recent reference is [Reference HartzHa].
$H\in \mathcal {RK}$
have and some do not. The class of H with that property is of fundamental importance in function-theoretic operator theory and is actively studied. Some background references are [Reference Agler and PickAM, Reference ArvesonAr, Reference Arcozzi, Rochberg, Sawyer and WickARSW2, Reference Shalit and AlpaySh]. A sample recent reference is [Reference HartzHa].
We will use the following definition of the CPP.
Definition 2.1 We will say a finite-dimensional RKHS H has the CPP if there is finite
![]() $X\subset \mathbb {CH}^{r}$
so that H is a rescaling of
$X\subset \mathbb {CH}^{r}$
so that H is a rescaling of
![]() $DA_{r}(X).$
$DA_{r}(X).$
This is very much a definition of convenience. The classical definition of the CPP is in terms of extension properties of multipliers. Using that classical definition neither the fact that for any X, we have
![]() $DA_{r}(X)\in \mathcal {CPP}$
nor the fact that any
$DA_{r}(X)\in \mathcal {CPP}$
nor the fact that any
![]() $H\in \mathcal {CPP}$
is a rescaling of a
$H\in \mathcal {CPP}$
is a rescaling of a
![]() $DA_{r}(X)$
is straightforward. The full story is in [Reference Agler and PickAM] where one can also find a characterization of
$DA_{r}(X)$
is straightforward. The full story is in [Reference Agler and PickAM] where one can also find a characterization of
![]() $H\in \mathcal {CPP}$
using the Gram matrix entries of
$H\in \mathcal {CPP}$
using the Gram matrix entries of
![]() $H.$
$H.$
If
![]() $H\in \mathcal {RK}$
has the CPP, then we write
$H\in \mathcal {RK}$
has the CPP, then we write
![]() $H\in \mathcal {CPP}$
. It is immediate that every
$H\in \mathcal {CPP}$
. It is immediate that every
![]() $DA_{r}(X)\in \mathcal {CPP}$
, and that the CPP is preserved by rescaling and inherited by regular subspaces.
$DA_{r}(X)\in \mathcal {CPP}$
, and that the CPP is preserved by rescaling and inherited by regular subspaces.
2.3 Invariants
Given
![]() $H\in \mathcal {RK}$
, we now define several numerical functions of tuples of elements of
$H\in \mathcal {RK}$
, we now define several numerical functions of tuples of elements of
![]() $RK(H)$
the set of reproducing kernels of
$RK(H)$
the set of reproducing kernels of
![]() $H.$
The definitions involve algebraic combinations of Gram matrix entries which by (2.5) are seen to be unchanged when H is replaced by a rescaling of
$H.$
The definitions involve algebraic combinations of Gram matrix entries which by (2.5) are seen to be unchanged when H is replaced by a rescaling of
![]() $H.$
Thus, the functions are rescaling invariants, well defined on the rescaling equivalence classes.
$H.$
Thus, the functions are rescaling invariants, well defined on the rescaling equivalence classes.
These functionals can also be regarded as defined for tuples of points in
![]() $\mathbb {CH}^{n}$
as follows. Given a functional F defined on, for instance, pairs of kernel functions, and given
$\mathbb {CH}^{n}$
as follows. Given a functional F defined on, for instance, pairs of kernel functions, and given
![]() $x,y\in \mathbb {CH}^{n}$
select by
$x,y\in \mathbb {CH}^{n}$
select by
![]() $X\subset \mathbb {CH}^{n}$
with
$X\subset \mathbb {CH}^{n}$
with
![]() $x,y\in X$
and set
$x,y\in X$
and set
![]() $F(x,y)=F(k_{x},k_{y})$
where
$F(x,y)=F(k_{x},k_{y})$
where
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
are the kernel functions in
$k_{y}$
are the kernel functions in
![]() $RK(DA(X)).$
It is straightforward to check that this value is independent of the choice of X (and we will not mention X again) and that if F acting on Hilbert spaces is rescaling invariant, then the “same” functional acting on
$RK(DA(X)).$
It is straightforward to check that this value is independent of the choice of X (and we will not mention X again) and that if F acting on Hilbert spaces is rescaling invariant, then the “same” functional acting on
![]() $\mathbb {CH}^{n}$
is automorphism invariant. We will use the same names and notation for the functionals acting on an
$\mathbb {CH}^{n}$
is automorphism invariant. We will use the same names and notation for the functionals acting on an
![]() $RK(H)$
and for the induced functionals acting on points in
$RK(H)$
and for the induced functionals acting on points in
![]() $\mathbb {CH}^{n}.$
$\mathbb {CH}^{n}.$
2.3.1 Distance
For
![]() $H\in \mathcal {RK}$
and
$H\in \mathcal {RK}$
and
![]() $h_{1}$
,
$h_{1}$
,
![]() $h_{2}\in RK(H)$
, we define
$h_{2}\in RK(H)$
, we define
![]() $\delta _{H}$
by
$\delta _{H}$
by
 $$ \begin{align} \delta_{H}(i,j)=\delta_{H}(h_{i},h_{j})=\sqrt{1-\frac{\left\vert h_{ij}\right\vert ^{2}}{h_{ii}h_{jj}}}=\sqrt{1-|\widehat{h_{ij}}|^{2}}. \end{align} $$
$$ \begin{align} \delta_{H}(i,j)=\delta_{H}(h_{i},h_{j})=\sqrt{1-\frac{\left\vert h_{ij}\right\vert ^{2}}{h_{ii}h_{jj}}}=\sqrt{1-|\widehat{h_{ij}}|^{2}}. \end{align} $$
This function is a metric on H ([Reference Agler and PickAM, Lemma 9.9], [Reference Arcozzi, Rochberg, Sawyer and WickARSW]) and is clearly invariant under rescaling. Using the scheme of the previous paragraphs, we can extend this definition to a functional, call it
![]() $\delta ^{\prime }$
for the moment, acting on pairs of points in
$\delta ^{\prime }$
for the moment, acting on pairs of points in
![]() $\mathbb {CH}^{n}.$
One of the main links between the Hilbert space theory and hyperbolic geometry is that
$\mathbb {CH}^{n}.$
One of the main links between the Hilbert space theory and hyperbolic geometry is that
![]() $\delta ^{\prime }$
equals the pseudohyperbolic distance,
$\delta ^{\prime }$
equals the pseudohyperbolic distance,
![]() $\delta ,$
between points, already defined in (2.1). To see this, use (2.3) and rewrite (2.4) as, for
$\delta ,$
between points, already defined in (2.1). To see this, use (2.3) and rewrite (2.4) as, for
![]() $w,x,y,z\in \mathbb {CH}^{n},$
$w,x,y,z\in \mathbb {CH}^{n},$
 $$ \begin{align} 1-\frac{k(w,y)k(y,z)}{k(y,y)k(w,z)}=\left\langle \left\langle \phi_{y} (z),\phi_{y}(w)\right\rangle \right\rangle. \end{align} $$
$$ \begin{align} 1-\frac{k(w,y)k(y,z)}{k(y,y)k(w,z)}=\left\langle \left\langle \phi_{y} (z),\phi_{y}(w)\right\rangle \right\rangle. \end{align} $$
Taking
![]() $z=w$
, we have
$z=w$
, we have
 $$ \begin{align} \delta^{2}(y,w)=\left\vert \phi_{y}(w)\right\vert ^{2}=1-\frac{\left\vert k(y,w)\right\vert ^{2}}{k(y,y)k(w,w)}=\delta^{\prime2}(y,w). \end{align} $$
$$ \begin{align} \delta^{2}(y,w)=\left\vert \phi_{y}(w)\right\vert ^{2}=1-\frac{\left\vert k(y,w)\right\vert ^{2}}{k(y,y)k(w,w)}=\delta^{\prime2}(y,w). \end{align} $$
The first equality in (2.8) is the definition of
![]() $\delta $
, the second is a special case of (2.7), and the third is the definition of
$\delta $
, the second is a special case of (2.7), and the third is the definition of
![]() $\delta ^{\prime 2}.$
Thus,
$\delta ^{\prime 2}.$
Thus,
![]() $\delta =\delta ^{\prime }.$
Alternatively, note that for any
$\delta =\delta ^{\prime }.$
Alternatively, note that for any
![]() $z\in \mathbb {B}_{n}$
, we have
$z\in \mathbb {B}_{n}$
, we have
![]() $\delta (0,z)=\left \vert z\right \vert =\delta ^{\prime }(0,z)$
and both
$\delta (0,z)=\left \vert z\right \vert =\delta ^{\prime }(0,z)$
and both
![]() $\delta $
and
$\delta $
and
![]() $\acute {\delta }^{\prime }$
are invariant under automorphisms; hence, the two metrics are equal. We now drop the notation
$\acute {\delta }^{\prime }$
are invariant under automorphisms; hence, the two metrics are equal. We now drop the notation
![]() $\delta ^{\prime }$
and simply write
$\delta ^{\prime }$
and simply write
![]() $\delta $
for the functional defined on RKHS and for the pseudohyperbolic metric. Using (2.7), we can express
$\delta $
for the functional defined on RKHS and for the pseudohyperbolic metric. Using (2.7), we can express
![]() $\delta $
in terms of coordinates; for
$\delta $
in terms of coordinates; for
![]() $y,w\in \mathbb {B}_{n}$
,
$y,w\in \mathbb {B}_{n}$
,
 $$ \begin{align} \delta^{2}(y,w)=1-\frac{(1-\left\langle \left\langle y,y\right\rangle \right\rangle )(1-\left\langle \left\langle w,w\right\rangle \right\rangle )}{\left\vert 1-\left\langle \left\langle y,w\right\rangle \right\rangle \right\vert ^{2}}. \end{align} $$
$$ \begin{align} \delta^{2}(y,w)=1-\frac{(1-\left\langle \left\langle y,y\right\rangle \right\rangle )(1-\left\langle \left\langle w,w\right\rangle \right\rangle )}{\left\vert 1-\left\langle \left\langle y,w\right\rangle \right\rangle \right\vert ^{2}}. \end{align} $$
2.3.2 Angular invariant
For
![]() $H\in \mathcal {RK}$
, we define the angular invariant
$H\in \mathcal {RK}$
, we define the angular invariant
![]() $\alpha $
by, for
$\alpha $
by, for
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
,
$k_{2}$
,
![]() $k_{3}\in RK(H),$
$k_{3}\in RK(H),$
(In general situations, care is needed in selecting a branch of
![]() $\arg .$
However, for
$\arg .$
However, for
![]() $k\in RK(DA(Z))$
,
$k\in RK(DA(Z))$
,
![]() $\operatorname {Re}k>0$
and that lets us avoid problems.) Notice that
$\operatorname {Re}k>0$
and that lets us avoid problems.) Notice that
![]() $\alpha $
satisfies a cocycle identity; if
$\alpha $
satisfies a cocycle identity; if
![]() $k_{4}$
is a fourth kernel function, then
$k_{4}$
is a fourth kernel function, then
We discuss some of the geometry associated with
![]() $\alpha $
in Section 4.4. More about this invariant is in [Reference Burger and IzzoBIM, Reference ClercC, Reference Clerc and ØrstedCO, Reference GoldmanGo, Reference Hangan and MasalaHM, Reference MonodM, Reference RochbergRo].
$\alpha $
in Section 4.4. More about this invariant is in [Reference Burger and IzzoBIM, Reference ClercC, Reference Clerc and ØrstedCO, Reference GoldmanGo, Reference Hangan and MasalaHM, Reference MonodM, Reference RochbergRo].
2.3.3
 $\mathbf {kos}$
$\mathbf {kos}$
For
![]() $H\in \mathcal {RK}$
, we define
$H\in \mathcal {RK}$
, we define
![]() $\operatorname *{kos}$
, a functional of triples of kernel functions. For
$\operatorname *{kos}$
, a functional of triples of kernel functions. For
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
,
$k_{2}$
,
![]() $k_{3}\in RK(H)$
,
$k_{3}\in RK(H)$
,
![]() $k_{1}\neq k_{2}$
,
$k_{1}\neq k_{2}$
,
![]() $k_{3},$
set
$k_{3},$
set
and note the symmetry
![]() $\operatorname *{kos}\nolimits _{1}(2,3)=\overline {\operatorname *{kos}\nolimits _{1}(3,2)}$
.
$\operatorname *{kos}\nolimits _{1}(2,3)=\overline {\operatorname *{kos}\nolimits _{1}(3,2)}$
.
If
![]() $H=DA(X)$
for some
$H=DA(X)$
for some
![]() $X\subset \mathbb {CH}^{n}$
, then
$X\subset \mathbb {CH}^{n}$
, then
![]() $\operatorname *{kos}$
is related to the geometry of
$\operatorname *{kos}$
is related to the geometry of
![]() $X.$
Recall that if
$X.$
Recall that if
![]() $x\in \mathbb {CH}^{n}$
, then
$x\in \mathbb {CH}^{n}$
, then
![]() $\phi _{x}$
is the ball involution which interchanges x and
$\phi _{x}$
is the ball involution which interchanges x and
![]() $0.$
We can use (2.7) and obtain
$0.$
We can use (2.7) and obtain
In particular, if
![]() $\xi $
is at the origin,
$\xi $
is at the origin,
![]() $\xi =\mathit {o}$
, then
$\xi =\mathit {o}$
, then
![]() $\phi _{\xi }$
is the identity, for any
$\phi _{\xi }$
is the identity, for any
![]() $w \ \phi _{\xi }(w)=w,$
and
$w \ \phi _{\xi }(w)=w,$
and
![]() $\delta (\xi ,w)=\delta (o,w)=\left \vert w\right \vert .$
In that case,
$\delta (\xi ,w)=\delta (o,w)=\left \vert w\right \vert .$
In that case,
 $$ \begin{align} \operatorname*{kos}\nolimits_{\mathit{o}}(y,z)=\left\langle \left\langle \frac{y}{\left\vert y\right\vert },\frac{z}{\left\vert z\right\vert }\right\rangle \right\rangle =\left\langle \left\langle \widehat{y} ,\widehat{z}\right\rangle \right\rangle. \end{align} $$
$$ \begin{align} \operatorname*{kos}\nolimits_{\mathit{o}}(y,z)=\left\langle \left\langle \frac{y}{\left\vert y\right\vert },\frac{z}{\left\vert z\right\vert }\right\rangle \right\rangle =\left\langle \left\langle \widehat{y} ,\widehat{z}\right\rangle \right\rangle. \end{align} $$
(Although
![]() $\operatorname *{kos}$
is invariant under automorphisms of
$\operatorname *{kos}$
is invariant under automorphisms of
![]() $\mathbb {B}_{n}$
, this formula is an inhomogenous representation and is not invariant.)
$\mathbb {B}_{n}$
, this formula is an inhomogenous representation and is not invariant.)
If the vectors y and z were in
![]() $\mathbb {R}^{n}$
, this would be the inner product of unit vectors in
$\mathbb {R}^{n}$
, this would be the inner product of unit vectors in
![]() $\mathbb {R}^{n}$
and would equal the cosine of the angle between the segments
$\mathbb {R}^{n}$
and would equal the cosine of the angle between the segments
![]() $\mathit {o}y$
and
$\mathit {o}y$
and
![]() $\mathit {o}z$
. That is the source of the name
$\mathit {o}z$
. That is the source of the name
![]() $\operatorname *{kos}.$
$\operatorname *{kos}.$
If
![]() $\dim H=n$
, then for
$\dim H=n$
, then for
![]() $1\leq s\leq n$
, we define the
$1\leq s\leq n$
, we define the
![]() $(n-1)\times (n-1)$
matrices
$(n-1)\times (n-1)$
matrices
 $$ \begin{align} \operatorname*{MQ}(H,s) & =\left( \delta_{si}\delta_{sj}\operatorname*{kos} \nolimits_{s}(i,j)\right) _{\substack{i,j=1\\i,j\neq s}}^{n}=\left( 1-\frac{k_{is}k_{sj}}{k_{ij}k_{ss}}\right) _{\substack{i,j=1\\i,j\neq s}}^{n}. \end{align} $$
$$ \begin{align} \operatorname*{MQ}(H,s) & =\left( \delta_{si}\delta_{sj}\operatorname*{kos} \nolimits_{s}(i,j)\right) _{\substack{i,j=1\\i,j\neq s}}^{n}=\left( 1-\frac{k_{is}k_{sj}}{k_{ij}k_{ss}}\right) _{\substack{i,j=1\\i,j\neq s}}^{n}. \end{align} $$
We also write
![]() $\operatorname *{KOS}(X,s)$
for
$\operatorname *{KOS}(X,s)$
for
![]() $\operatorname *{KOS}(DA(X),s).$
$\operatorname *{KOS}(DA(X),s).$
2.4 Matrix notation
For an
![]() $n\times n$
matrix A, we write
$n\times n$
matrix A, we write
![]() $A\succ 0$
if A is positive definite and
$A\succ 0$
if A is positive definite and
![]() $A\succcurlyeq 0$
if it is positive semidefinite. We say B is a principal submatrix of A if it is obtained from A by removing certain rows and also the corresponding columns. Note that if
$A\succcurlyeq 0$
if it is positive semidefinite. We say B is a principal submatrix of A if it is obtained from A by removing certain rows and also the corresponding columns. Note that if
![]() $H\in $
$H\in $
![]() $\mathcal {RK}$
, then J is a regular subspace of H if and only if
$\mathcal {RK}$
, then J is a regular subspace of H if and only if
![]() $\operatorname *{Gr}(J)$
is a principal submatrix of
$\operatorname *{Gr}(J)$
is a principal submatrix of
![]() $\operatorname *{Gr}(H)$
. We denote the set of all principal submatrices of A by
$\operatorname *{Gr}(H)$
. We denote the set of all principal submatrices of A by
![]() $\mathcal {PS} {\large (A).}$
If
$\mathcal {PS} {\large (A).}$
If
![]() $B\in \mathcal {PS}{\large (A)}$
and the indices of the rows and columns retained in B are an initial segment, indices j with
$B\in \mathcal {PS}{\large (A)}$
and the indices of the rows and columns retained in B are an initial segment, indices j with
![]() $1\leq j\leq k$
for some
$1\leq j\leq k$
for some
![]() $k\leq n,$
then B is said to be a leading principal submatrix. The determinants of those matrices are called principal minors and leading principal minors, respectively.
$k\leq n,$
then B is said to be a leading principal submatrix. The determinants of those matrices are called principal minors and leading principal minors, respectively.
3 The
 $\mathcal {CPP}$
and point sets in
$\mathcal {CPP}$
and point sets in
 $\mathbb {CH}^{n}$
$\mathbb {CH}^{n}$
We will sometimes use a model triangle
![]() $\Gamma $
or a model tetrahedron
$\Gamma $
or a model tetrahedron
![]() $\Delta $
which have convenient coordinates. Our model triangle is
$\Delta $
which have convenient coordinates. Our model triangle is
![]() $\Gamma \subset \mathbb {CH}^{2}$
:
$\Gamma \subset \mathbb {CH}^{2}$
:
 $$ \begin{align} & \Gamma=\left\{ x_{1},x_{2},x_{3}\right\} =\left\{ (0,0\},(a,0),(x,b)\right\} ,\\ & a>0,b\geq0\text{, } \ x\in\mathbb{C},\nonumber\\ & 0<a,\text{ }\left\vert x\right\vert ^{2}+b^{2}<1.\nonumber \end{align} $$
$$ \begin{align} & \Gamma=\left\{ x_{1},x_{2},x_{3}\right\} =\left\{ (0,0\},(a,0),(x,b)\right\} ,\\ & a>0,b\geq0\text{, } \ x\in\mathbb{C},\nonumber\\ & 0<a,\text{ }\left\vert x\right\vert ^{2}+b^{2}<1.\nonumber \end{align} $$
Our model tetrahedron is
![]() $\Delta \subset \mathbb {CH}^{3}$
:
$\Delta \subset \mathbb {CH}^{3}$
:
 $$ \begin{align} &\Delta=\left\{ x_{1},x_{2},x_{3},x_{4}\right\} =\left\{(0,0,0),(a,0,0),(x,b,0),(y,z,c)\right\},\\ &a>0,\text{ }b,c\geq0,\text{ }x,y,z\in\mathbb{C}\text{, } \ \nonumber \\ & 0<\left\vert a\right\vert ^{2},\text{ }\left\vert x\right\vert{}^{2}+\left\vert b\right\vert ^{2},\text{ }\left\vert y\right\vert{}^{2}+\left\vert z\right\vert ^{2}+\left\vert c\right\vert ^{2}<1.\nonumber\end{align} $$
$$ \begin{align} &\Delta=\left\{ x_{1},x_{2},x_{3},x_{4}\right\} =\left\{(0,0,0),(a,0,0),(x,b,0),(y,z,c)\right\},\\ &a>0,\text{ }b,c\geq0,\text{ }x,y,z\in\mathbb{C}\text{, } \ \nonumber \\ & 0<\left\vert a\right\vert ^{2},\text{ }\left\vert x\right\vert{}^{2}+\left\vert b\right\vert ^{2},\text{ }\left\vert y\right\vert{}^{2}+\left\vert z\right\vert ^{2}+\left\vert c\right\vert ^{2}<1.\nonumber\end{align} $$
It is easy to check that any triangle in
![]() $\mathbb {CH}^{n},$
once the numbering of the vertices is fixed, is congruent to a unique
$\mathbb {CH}^{n},$
once the numbering of the vertices is fixed, is congruent to a unique
![]() $\Gamma $
; similarly for tetrahedra and
$\Gamma $
; similarly for tetrahedra and
![]() $\Delta $
.
$\Delta $
.
To a three-dimensional
![]() $H\in \mathcal {RK}$
with
$H\in \mathcal {RK}$
with
![]() $RK(H)=\left \{ h_{i}\right \} _{i=1}^{3}$
, we associate the following sets of invariant quantities:
$RK(H)=\left \{ h_{i}\right \} _{i=1}^{3}$
, we associate the following sets of invariant quantities:
 $$ \begin{align} S & =\left\{ |\widehat{h_{12}}|,\text{ }|\widehat{h_{23}}|\text{, }|\widehat{h_{13}}|\text{, }\mathbb{\alpha}_{123}\right\} ,\nonumber\\ S^{\prime} & =\left\{ \delta_{12},\text{ }\delta_{13},\text{ }\delta _{23}\text{, }\mathbb{\alpha}_{123}\right\} ,\nonumber\\ S^{\prime\prime} & =\{\delta_{12},\delta_{13},\operatorname*{kos} \nolimits_{1}(2,3)\}. \end{align} $$
$$ \begin{align} S & =\left\{ |\widehat{h_{12}}|,\text{ }|\widehat{h_{23}}|\text{, }|\widehat{h_{13}}|\text{, }\mathbb{\alpha}_{123}\right\} ,\nonumber\\ S^{\prime} & =\left\{ \delta_{12},\text{ }\delta_{13},\text{ }\delta _{23}\text{, }\mathbb{\alpha}_{123}\right\} ,\nonumber\\ S^{\prime\prime} & =\{\delta_{12},\delta_{13},\operatorname*{kos} \nolimits_{1}(2,3)\}. \end{align} $$
And, for convenience, we set
 $$ \begin{align} \Gamma_{abc}=\left\vert \frac{\widehat{h_{ab}}\widehat{h_{bc}}} {\widehat{h_{ca}}}\right\vert =\sqrt{\frac{(1-\delta_{H}^{2}(a,b))\,(1-\delta _{H}^{2}(b,c))}{(1-\delta_{H}^{2}(c,a))}.} \end{align} $$
$$ \begin{align} \Gamma_{abc}=\left\vert \frac{\widehat{h_{ab}}\widehat{h_{bc}}} {\widehat{h_{ca}}}\right\vert =\sqrt{\frac{(1-\delta_{H}^{2}(a,b))\,(1-\delta _{H}^{2}(b,c))}{(1-\delta_{H}^{2}(c,a))}.} \end{align} $$
The following describes three-point sets X in
![]() $\mathbb {CH}^{2}$
and the associated
$\mathbb {CH}^{2}$
and the associated
![]() $DA(X)$
spaces.
$DA(X)$
spaces.
Theorem 3.1 [Reference Agler and PickAM, Reference BrehmBr, Reference RochbergRo]
Given a three-dimensional
![]() $H\in \mathcal {RK}$
, the following are equivalent:
$H\in \mathcal {RK}$
, the following are equivalent:
-
(1)
 $H\in \mathcal {CPP}$
.
$H\in \mathcal {CPP}$
. -
(2) There is a three-point set X in
 $\mathbb {CH}^{2}$
with
$\mathbb {CH}^{2}$
with
 $H\sim DA(X).$
$H\sim DA(X).$
-
(3) There is a
 $\Gamma $
as in (3.1) with
$\Gamma $
as in (3.1) with
 $H\sim DA(\Gamma ).$
$H\sim DA(\Gamma ).$
-
(4) Let J be the regular subspace of H spanned by
 $\{h_{1}$
,
$\{h_{1}$
,
 $h_{2}\}.$
Let M be the multiplier on J of norm one specified by the following action of its adjoint:
$h_{2}\}.$
Let M be the multiplier on J of norm one specified by the following action of its adjoint:  $$ \begin{align*} M^{\ast}h_{1} & =0,\\ M^{\ast}h_{2} & =\delta_{H}(h_{1},h_{2})h_, \end{align*} $$
$$ \begin{align*} M^{\ast}h_{1} & =0,\\ M^{\ast}h_{2} & =\delta_{H}(h_{1},h_{2})h_, \end{align*} $$
then M extends to a multiplier of norm one on
 $H.$
$H.$
-
(5)
 $\operatorname *{KOS}(H,1)\succcurlyeq 0$
.
$\operatorname *{KOS}(H,1)\succcurlyeq 0$
. -
(6)
(3.5) $$ \begin{align} _{.\text{ }}\left\vert \operatorname*{kos}\nolimits_{1}(2,3)\right\vert \leq1. \end{align} $$
$$ \begin{align} _{.\text{ }}\left\vert \operatorname*{kos}\nolimits_{1}(2,3)\right\vert \leq1. \end{align} $$
-
(7) S and the
 $\Gamma $
’s defined from S using (3.4) satisfy (3.6)
$\Gamma $
’s defined from S using (3.4) satisfy (3.6) $$ \begin{align} \Gamma_{123}+\Gamma_{231}+\Gamma_{312}\leq2\cos\mathbb{\alpha}_{123}. \end{align} $$
$$ \begin{align} \Gamma_{123}+\Gamma_{231}+\Gamma_{312}\leq2\cos\mathbb{\alpha}_{123}. \end{align} $$
-
(8)
 $S^{\prime }$
and the
$S^{\prime }$
and the
 $\Gamma $
’s defined from
$\Gamma $
’s defined from
 $S^{\prime }$
using (3.4) satisfy (3.6).
$S^{\prime }$
using (3.4) satisfy (3.6).
Furthermore, X sits inside a complex geodesic if and only if
![]() $\det \operatorname *{KOS}(H,1)=0,$
or equivalently
$\det \operatorname *{KOS}(H,1)=0,$
or equivalently
![]() $\left \vert \operatorname *{kos} \nolimits _{1}(2,3)\right \vert =1,$
or the b coordinate of
$\left \vert \operatorname *{kos} \nolimits _{1}(2,3)\right \vert =1,$
or the b coordinate of
![]() $\Gamma $
in (3.1) is
$\Gamma $
in (3.1) is
![]() $0.$
It sits inside a totally real geodesic submanifold of real dimension 2 if and only if
$0.$
It sits inside a totally real geodesic submanifold of real dimension 2 if and only if
![]() $\operatorname *{kos}\nolimits _{1}(2,3)$
is real.
$\operatorname *{kos}\nolimits _{1}(2,3)$
is real.
Conversely, given
data S and
![]() $\Gamma $
’s defined from S using (3.4) such that (3.6) holds,
$\Gamma $
’s defined from S using (3.4) such that (3.6) holds,
or
data
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $\Gamma $
’s defined from
$\Gamma $
’s defined from
![]() $S^{\prime }$
using (3.4) such that (3.6) holds,
$S^{\prime }$
using (3.4) such that (3.6) holds,
or
data
![]() $S^{\prime \prime } \ f$
or which (3.5) holds,
$S^{\prime \prime } \ f$
or which (3.5) holds,
there is triangle X in
![]() $\mathbb {CH}^{2},$
unique up to congruence, which has those parameters.
$\mathbb {CH}^{2},$
unique up to congruence, which has those parameters.
Proof The equivalence of the first two statements is by definition. The equivalence of statements (2)–(6) is in [Reference RochbergRo]. Statement (7) and the parts of (8) about existence of the triangle are due to Brehm [Reference BrehmBr]. The statement about X being in a complex geodesic is implicit in the proof of Theorem 16 in [Reference RochbergRo].
Thus, each of S,
![]() $S^{\prime },$
or
$S^{\prime },$
or
![]() $S^{\prime \prime }$
could be used to describe a triangle. The equivalence of using S or
$S^{\prime \prime }$
could be used to describe a triangle. The equivalence of using S or
![]() $S^{\prime }$
is clear. Passing between
$S^{\prime }$
is clear. Passing between
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S^{\prime \prime }$
is described in Section 4.2.
$S^{\prime \prime }$
is described in Section 4.2.
Remark 1 We will see in Proposition 4.5 that the value of
![]() $\operatorname *{kos}$
determines the congruence class of a vertex. Hence, the fact that the parameters in
$\operatorname *{kos}$
determines the congruence class of a vertex. Hence, the fact that the parameters in
![]() $S^{\prime \prime }$
determine the congruence class of a complex triangle is an analog of the fact that two side lengths and the shape of the included angle determine the congruence class of a Euclidean triangle.
$S^{\prime \prime }$
determine the congruence class of a complex triangle is an analog of the fact that two side lengths and the shape of the included angle determine the congruence class of a Euclidean triangle.
Some aspects of the previous theorem extend to larger sets and spaces. The next result is an amalgam of the fact that up to rescaling the
![]() $H\in \mathcal {CPP}$
are exactly the spaces
$H\in \mathcal {CPP}$
are exactly the spaces
![]() $DA(X)$
for X a finite set in
$DA(X)$
for X a finite set in
![]() $\mathbb {CH}^{n}$
[Reference Agler and PickAM], the fact mentioned earlier that automorphisms of the ball induce rescalings of spaces
$\mathbb {CH}^{n}$
[Reference Agler and PickAM], the fact mentioned earlier that automorphisms of the ball induce rescalings of spaces
![]() $DA(X),$
and the description of congruence classes of finite sets in
$DA(X),$
and the description of congruence classes of finite sets in
![]() $\mathbb {CH}^{n}$
given in [Reference Brehm and Et-TaouiBE, Reference GusevskiiG, Reference Hakim and SandlerHS, Reference RochbergRo].
$\mathbb {CH}^{n}$
given in [Reference Brehm and Et-TaouiBE, Reference GusevskiiG, Reference Hakim and SandlerHS, Reference RochbergRo].
Theorem 3.2 An n-dimensional
![]() $H\in \mathcal {RK}$
satisfies
$H\in \mathcal {RK}$
satisfies
![]() $H\in \mathcal {CPP}$
if and only if there is an
$H\in \mathcal {CPP}$
if and only if there is an
![]() $X=\left \{ x_{i}\right \} _{1}^{n}\subset \mathbb {CH}^{n-1}\ with \ H\sim DA(X).$
$X=\left \{ x_{i}\right \} _{1}^{n}\subset \mathbb {CH}^{n-1}\ with \ H\sim DA(X).$
![]() $Given$
another n-dimensional
$Given$
another n-dimensional
![]() $H^{\prime }\in \mathcal {CPP}$
with
$H^{\prime }\in \mathcal {CPP}$
with
![]() $H^{\prime }\sim DA(X^{\prime })$
for
$H^{\prime }\sim DA(X^{\prime })$
for
![]() $X^{\prime }=\left \{ x_{i}^{\prime }\right \} _{1}^{n}\subset \mathbb {CH}^{n-1}$
, the following are equivalent:
$X^{\prime }=\left \{ x_{i}^{\prime }\right \} _{1}^{n}\subset \mathbb {CH}^{n-1}$
, the following are equivalent:
-
(1)
 $H \ \sim H^{\prime }.$
$H \ \sim H^{\prime }.$
-
(2)
 $X\sim X^{\prime }.$
$X\sim X^{\prime }.$
-
(3) DA(
 $X)\sim DA(X^{\prime }).$
$X)\sim DA(X^{\prime }).$
-
(4) All the triangles of X are congruent to the triangles of
 $X^{\prime }$
; i.e., for each triple
$X^{\prime }$
; i.e., for each triple
 $i,j,k$
,
$i,j,k$
,
 $1\leq \ i$
, j,
$1\leq \ i$
, j,
 $k\leq n$
, there is a ball automorphisms taking
$k\leq n$
, there is a ball automorphisms taking
 $\{x_{i}$
,
$\{x_{i}$
,
 $x_{j}$
,
$x_{j}$
,
 $x_{k}\}$
to
$x_{k}\}$
to
 $\{x_{i}^{\prime },$
$\{x_{i}^{\prime },$
 $x_{j}^{\prime }$
,
$x_{j}^{\prime }$
,
 $x_{k}^{\prime }\}.$
$x_{k}^{\prime }\}.$
-
(5) The triangles of X which have one vertex at
 $x_{1}$
are congruent to the corresponding triangles of
$x_{1}$
are congruent to the corresponding triangles of
 $X^{\prime }$
; for each pair
$X^{\prime }$
; for each pair
 $i,j$
,
$i,j$
,
 $1<i<j\leq n$
, the triangles
$1<i<j\leq n$
, the triangles
 $\{x_{1}$
,
$\{x_{1}$
,
 $x_{i}$
,
$x_{i}$
,
 $x_{j}\}$
and
$x_{j}\}$
and
 $\{x_{1}^{\prime },$
$\{x_{1}^{\prime },$
 $x_{i}^{\prime }$
,
$x_{i}^{\prime }$
,
 $x_{j}^{`\prime }\}$
are congruent.
$x_{j}^{`\prime }\}$
are congruent. -
(6) The regular three-dimensional subspaces of H are rescalings of the corresponding regular three-dimensional subspaces of
 $H^{\prime }.$
$H^{\prime }.$
-
(7) The regular three-dimensional subspaces of H which contain
 $k_{x_{1}}$
are rescalings of the corresponding three-dimensional subspaces of
$k_{x_{1}}$
are rescalings of the corresponding three-dimensional subspaces of
 $H^{\prime }.$
$H^{\prime }.$
Corollary 3.3 The relationship
![]() $H\sim DA(X)$
establishes a bijection between the class of n-dimensional
$H\sim DA(X)$
establishes a bijection between the class of n-dimensional
![]() $H\in \mathcal {CPP}$
modulo rescaling and the class of n point sets X in
$H\in \mathcal {CPP}$
modulo rescaling and the class of n point sets X in
![]() $\mathbb {CH}^{k}$
,
$\mathbb {CH}^{k}$
,
![]() $k\geq n-1,$
modulo congruence. The correspondence respects passage to regular subspaces and to subsets.
$k\geq n-1,$
modulo congruence. The correspondence respects passage to regular subspaces and to subsets.
If we use S,
![]() $S^{\prime }$
, or
$S^{\prime }$
, or
![]() $S^{\prime \prime }$
to characterize the triangles in (4) of the theorem, we obtain
$S^{\prime \prime }$
to characterize the triangles in (4) of the theorem, we obtain
![]() $O(n^{3})$
real numbers which describe X up to congruence. However, that list has repetitions and redundancies. Restricting to the triangles listed in (5) and noting that some side lengths are listed twice leads to a list of
$O(n^{3})$
real numbers which describe X up to congruence. However, that list has repetitions and redundancies. Restricting to the triangles listed in (5) and noting that some side lengths are listed twice leads to a list of
![]() $\left ( n-1\right ) ^{2}$
real parameters which determine X up to congruence. That number is optimal; triangles are determined by four parameters, tetrahedra by nine. There are also constraints on the parameters; the inequality (3.6) for triangles is the simplest example. We give analogous constraints for tetrahedra in Theorem 6.2. Also, noting the previous corollary, the same parameters (or, perhaps, similarly named parameters) describe spaces
$\left ( n-1\right ) ^{2}$
real parameters which determine X up to congruence. That number is optimal; triangles are determined by four parameters, tetrahedra by nine. There are also constraints on the parameters; the inequality (3.6) for triangles is the simplest example. We give analogous constraints for tetrahedra in Theorem 6.2. Also, noting the previous corollary, the same parameters (or, perhaps, similarly named parameters) describe spaces
![]() $DA(X)$
and spaces in
$DA(X)$
and spaces in
![]() $\mathcal {CPP}$
.
$\mathcal {CPP}$
.
3.1 Assembly and coherence
We might know that each of several spaces
![]() $\left \{ J_{i}\right \} $
is equivalent under rescaling to a subspace
$\left \{ J_{i}\right \} $
is equivalent under rescaling to a subspace
![]() $H_{i}$
of some
$H_{i}$
of some
![]() $H; \ J_{i}\leadsto H_{i}\subset H.$
In that case, there are coherence conditions connecting the
$H; \ J_{i}\leadsto H_{i}\subset H.$
In that case, there are coherence conditions connecting the
![]() $\left \{ J_{i}\right \} $
; if
$\left \{ J_{i}\right \} $
; if
![]() $H_{i}\cap H_{j}=H_{ij}$
, then the corresponding subspaces,
$H_{i}\cap H_{j}=H_{ij}$
, then the corresponding subspaces,
![]() $J_{i(j)}\subset J_{i}$
which corresponds to
$J_{i(j)}\subset J_{i}$
which corresponds to
![]() $H_{ij}$
and
$H_{ij}$
and
![]() $J_{j(i)} \ \subset \ J_{j}$
which also corresponds to
$J_{j(i)} \ \subset \ J_{j}$
which also corresponds to
![]() $H_{ij}$
, must be rescalings of each other. This condition is nontrivial if
$H_{ij}$
, must be rescalings of each other. This condition is nontrivial if
![]() $\dim H_{ij}>1.$
If these conditions are met, then the
$\dim H_{ij}>1.$
If these conditions are met, then the
![]() $\left \{ J_{i}\right \} $
are said to be a coherent set of spaces and we will write
$\left \{ J_{i}\right \} $
are said to be a coherent set of spaces and we will write
![]() $\left \{ J_{i}\right \} \rightrightarrows \,H$
.
$\left \{ J_{i}\right \} \rightrightarrows \,H$
.
Here is how this works in the context of Question 2. For a four-dimensional
![]() $H\in \mathcal {CPP}$
with
$H\in \mathcal {CPP}$
with
![]() $RK(H)=\left \{ h_{i}\right \} _{i=1}^{4}$
, denote the four regular three-dimensional subspaces
$RK(H)=\left \{ h_{i}\right \} _{i=1}^{4}$
, denote the four regular three-dimensional subspaces
![]() $\left \{ H_{i}\right \} _{i=1}^{4}$
by
$\left \{ H_{i}\right \} _{i=1}^{4}$
by
Question 2 asks for necessary and sufficient conditions on four three-dimensional spaces
![]() $\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {RK}$
to insure that there is an
$\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {RK}$
to insure that there is an
![]() $H\in \mathcal {CPP}$
with for
$H\in \mathcal {CPP}$
with for
![]() $1\leq i\leq 4,$
$1\leq i\leq 4,$
![]() $H_{i}\sim J_{i}.$
If there are such rescalings, then we suppose the indices on the reproducing kernels
$H_{i}\sim J_{i}.$
If there are such rescalings, then we suppose the indices on the reproducing kernels
![]() $j_{ir}$
of
$j_{ir}$
of
![]() $J_{i}$
have been chosen so that for each
$J_{i}$
have been chosen so that for each
![]() $i,r$
, the rescaling of
$i,r$
, the rescaling of
![]() $H_{i}$
and
$H_{i}$
and
![]() $J_{i}$
matches the kernel function
$J_{i}$
matches the kernel function
![]() $h_{r}$
of
$h_{r}$
of
![]() $H_{i}$
with the kernel function
$H_{i}$
with the kernel function
![]() $j_{ir}$
of
$j_{ir}$
of
![]() $J_{i}.$
$J_{i}.$
If
![]() $\left \{ J_{i}\right \} $
is a coherent set of spaces, then the space
$\left \{ J_{i}\right \} $
is a coherent set of spaces, then the space
![]() $J_{1},$
with kernel functions
$J_{1},$
with kernel functions
![]() $\left \{ j_{12},j_{13},j_{14}\right \} ,$
is a rescaling of
$\left \{ j_{12},j_{13},j_{14}\right \} ,$
is a rescaling of
![]() $H_{1}$
which has kernel functions
$H_{1}$
which has kernel functions
![]() $\left \{ h_{2},h_{3} ,h_{4}\right \} $
with
$\left \{ h_{2},h_{3} ,h_{4}\right \} $
with
![]() $j_{1s}$
pairing with
$j_{1s}$
pairing with
![]() $h_{s};$
similarly for
$h_{s};$
similarly for
![]() $J_{3}$
with kernels
$J_{3}$
with kernels
![]() $\left \{ j_{31},j_{32},j_{34}\right \} $
and
$\left \{ j_{31},j_{32},j_{34}\right \} $
and
![]() $H_{3}$
with kernels
$H_{3}$
with kernels
![]() $\left \{ h_{1},h_{2},h_{4}\right \} .$
Thus, subspace
$\left \{ h_{1},h_{2},h_{4}\right \} .$
Thus, subspace
![]() $J_{1,24}$
of
$J_{1,24}$
of
![]() $J_{1}$
with kernel functions
$J_{1}$
with kernel functions
![]() $\left \{ j_{12},j_{14}\right \} $
and the subspace
$\left \{ j_{12},j_{14}\right \} $
and the subspace
![]() $J_{3,24}$
of
$J_{3,24}$
of
![]() $J_{3}$
with kernel functions
$J_{3}$
with kernel functions
![]() $\left \{ j_{32} ,j_{34}\right \} $
are both rescalings of the subspace of
$\left \{ j_{32} ,j_{34}\right \} $
are both rescalings of the subspace of
![]() $H_{24}$
with kernel functions
$H_{24}$
with kernel functions
![]() $\left \{ h_{2},h_{4}\right \} ,$
and hence
$\left \{ h_{2},h_{4}\right \} ,$
and hence
![]() $J_{1,24}\sim J_{3,24}.$
The other coherence conditions are all of this form; given
$J_{1,24}\sim J_{3,24}.$
The other coherence conditions are all of this form; given
![]() $p<q,r<s$
distinct elements of
$p<q,r<s$
distinct elements of
![]() $\left \{ 1,2,3,4\right \} $
, we must have
$\left \{ 1,2,3,4\right \} $
, we must have
![]() $J_{p,rs}\sim J_{q,rs}.$
These conditions are necessary for there to be rescalings of
$J_{p,rs}\sim J_{q,rs}.$
These conditions are necessary for there to be rescalings of
![]() $\left \{ J_{i}\right \} $
into
$\left \{ J_{i}\right \} $
into
![]() $H.$
These conditions are the Hilbert space analogs of the matching side length conditions necessary to assemble triangles into a tetrahedron.
$H.$
These conditions are the Hilbert space analogs of the matching side length conditions necessary to assemble triangles into a tetrahedron.
Notice that the conditions we obtained just now,
![]() $J_{p,rs}\sim J_{q,rs},$
did not involve the space H and in fact we can have a coherent set of spaces
$J_{p,rs}\sim J_{q,rs},$
did not involve the space H and in fact we can have a coherent set of spaces
![]() $\left \{ J_{i}\right \} $
without having an
$\left \{ J_{i}\right \} $
without having an
![]() $H.$
It suffices to have a consistent set of coherence conditions, statements that certain subspaces of the various
$H.$
It suffices to have a consistent set of coherence conditions, statements that certain subspaces of the various
![]() $\left \{ J_{i}\right \} $
are rescalings of each other. The consistency requirement is that the set of specified rescalings must be compatible with the fact that rescaling is an equivalence relation which interacts coherently with passage to subspaces. That is automatic if
$\left \{ J_{i}\right \} $
are rescalings of each other. The consistency requirement is that the set of specified rescalings must be compatible with the fact that rescaling is an equivalence relation which interacts coherently with passage to subspaces. That is automatic if
![]() $\left \{ J_{i}\right \} \rightrightarrows \,H$
but is also possible otherwise. In that case, we still call the
$\left \{ J_{i}\right \} \rightrightarrows \,H$
but is also possible otherwise. In that case, we still call the
![]() $\left \{ J_{i}\right \} $
a coherent set of spaces and we will write
$\left \{ J_{i}\right \} $
a coherent set of spaces and we will write
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??.$
$\left \{ J_{i}\right \} \rightrightarrows \,??.$
Thus, the statement
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??$
is the statement that there is a description (perhaps only implicit) of a type of target space H and an assembly scheme for constructing such an
$\left \{ J_{i}\right \} \rightrightarrows \,??$
is the statement that there is a description (perhaps only implicit) of a type of target space H and an assembly scheme for constructing such an
![]() $H.$
The statement
$H.$
The statement
![]() $\left \{ J_{i}\right \} \rightrightarrows H$
is that there is such an
$\left \{ J_{i}\right \} \rightrightarrows H$
is that there is such an
![]() $H.$
$H.$
Given
![]() $\left \{ J_{i}\right \} \rightrightarrows H$
, we would like to obtain information about H from the spaces
$\left \{ J_{i}\right \} \rightrightarrows H$
, we would like to obtain information about H from the spaces
![]() $\left \{ J_{i}\right \} $
together with the coherence data
$\left \{ J_{i}\right \} $
together with the coherence data
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??.$
We know from Theorem 3.2 that the values of
$\left \{ J_{i}\right \} \rightrightarrows \,??.$
We know from Theorem 3.2 that the values of
![]() $\delta _{ij}$
and
$\delta _{ij}$
and
![]() $\operatorname *{kos}_{i}(j,k)$
for H describe H up to rescaling and would like to compute them from the
$\operatorname *{kos}_{i}(j,k)$
for H describe H up to rescaling and would like to compute them from the
![]() $\left \{ J_{i}\right \} .$
Given
$\left \{ J_{i}\right \} .$
Given
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??$
, we can construct the imputed value of
$\left \{ J_{i}\right \} \rightrightarrows \,??$
, we can construct the imputed value of
![]() $\delta _{H}(a,b)$
by selecting any
$\delta _{H}(a,b)$
by selecting any
![]() $J_{s}$
whose image under the rescaling
$J_{s}$
whose image under the rescaling
![]() $J_{s}\leadsto H$
contains the kernel functions
$J_{s}\leadsto H$
contains the kernel functions
![]() $h_{a}$
and
$h_{a}$
and
![]() $h_{b}$
of
$h_{b}$
of
![]() $RK(H).$
If
$RK(H).$
If
![]() $j_{ra}$
and
$j_{ra}$
and
![]() $j_{rb}$
are the elements of
$j_{rb}$
are the elements of
![]() $RK(J_{s})$
which correspond to
$RK(J_{s})$
which correspond to
![]() $h_{a}$
and
$h_{a}$
and
![]() $h_{b}$
under that rescaling map, then
$h_{b}$
under that rescaling map, then
![]() $\delta _{J_{r}}(j_{ra},j_{rb})$
is our candidate value for
$\delta _{J_{r}}(j_{ra},j_{rb})$
is our candidate value for
![]() $\delta _{H}(a,b).$
Note that this is defined even if there is no H; however, if there is an H, then the rescaling
$\delta _{H}(a,b).$
Note that this is defined even if there is no H; however, if there is an H, then the rescaling
![]() $J_{s}\leadsto H$
insures that this value is
$J_{s}\leadsto H$
insures that this value is
![]() $\delta _{H}(a,b).$
Also, if there is another possible choice for
$\delta _{H}(a,b).$
Also, if there is another possible choice for
![]() $J_{s}$
, then the coherence conditions insure that choice will produce the same value of
$J_{s}$
, then the coherence conditions insure that choice will produce the same value of
![]() $\delta $
. If there is no such
$\delta $
. If there is no such
![]() $J_{s}$
, then we have no candidate for the value
$J_{s}$
, then we have no candidate for the value
![]() $\delta _{H}(a,b)$
and that value would be a free variable in our analysis; the free variable
$\delta _{H}(a,b)$
and that value would be a free variable in our analysis; the free variable
![]() $K_{42}$
in Corollary 6.3 is an example. The procedure for constructing our candidate values for
$K_{42}$
in Corollary 6.3 is an example. The procedure for constructing our candidate values for
![]() $\operatorname *{kos}_{a}(b,c)$
is the same except that we need to select a
$\operatorname *{kos}_{a}(b,c)$
is the same except that we need to select a
![]() $J_{s}$
whose image would contain the three elements of
$J_{s}$
whose image would contain the three elements of
![]() $RK(H)$
with indices
$RK(H)$
with indices
![]() $a,b,$
and
$a,b,$
and
![]() $c.$
$c.$
The general pattern is that given
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??$
, we can use the coherence data and compute (some of) the entries
$\left \{ J_{i}\right \} \rightrightarrows \,??$
, we can use the coherence data and compute (some of) the entries
![]() $\operatorname *{kos}_{a}(b,c)$
that the matrix
$\operatorname *{kos}_{a}(b,c)$
that the matrix
![]() $\operatorname *{KOS}(H,a)$
will have if there is an H with
$\operatorname *{KOS}(H,a)$
will have if there is an H with
![]() $\left \{ J_{i}\right \} \rightrightarrows \,H.$
(We are supposing that it has been specified which kernel functions (if any) of the spaces
$\left \{ J_{i}\right \} \rightrightarrows \,H.$
(We are supposing that it has been specified which kernel functions (if any) of the spaces
![]() $J_{i}$
are to be associated with the distinguished kernel
$J_{i}$
are to be associated with the distinguished kernel
![]() $k_{a}$
in
$k_{a}$
in
![]() $H.)$
We denote the partially defined matrix computed this way by
$H.)$
We denote the partially defined matrix computed this way by
![]() $\operatorname *{KOS}(\left \{ J_{i}\right \} ,a).$
If
$\operatorname *{KOS}(\left \{ J_{i}\right \} ,a).$
If
![]() $\left \{ J_{i}\right \} \rightrightarrows \,H$
, then
$\left \{ J_{i}\right \} \rightrightarrows \,H$
, then
![]() $\operatorname *{KOS}(\left \{ J_{i}\right \} ,a)=\operatorname *{KOS}(H,a).$
In Section 5.1, we give necessary and sufficient conditions on a matrix for it to be
$\operatorname *{KOS}(\left \{ J_{i}\right \} ,a)=\operatorname *{KOS}(H,a).$
In Section 5.1, we give necessary and sufficient conditions on a matrix for it to be
![]() $\operatorname *{KOS}(H,a)$
for an
$\operatorname *{KOS}(H,a)$
for an
![]() $H\in \mathcal {CPP}$
. Those conditions applied to
$H\in \mathcal {CPP}$
. Those conditions applied to
![]() $\operatorname *{KOS} (\left \{ J_{i}\right \} ,a)$
give necessary and sufficient conditions for the assembly question
$\operatorname *{KOS} (\left \{ J_{i}\right \} ,a)$
give necessary and sufficient conditions for the assembly question
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??$
to have a positive solution.
$\left \{ J_{i}\right \} \rightrightarrows \,??$
to have a positive solution.
By Corollary 3.3, statements about spaces, subspaces, rescalings, values of invariants, and coherence are equivalent to statements about sets in
![]() $\mathbb {CH}^{m},$
subsets, congruences, values of invariants, and an appropriate notion of coherence. We will use the same language and notation in both contexts. For instance, given sets
$\mathbb {CH}^{m},$
subsets, congruences, values of invariants, and an appropriate notion of coherence. We will use the same language and notation in both contexts. For instance, given sets
![]() $\left \{ Y_{i}\right \} $
in
$\left \{ Y_{i}\right \} $
in
![]() $\mathbb {CH}^{n}$
, we will write
$\mathbb {CH}^{n}$
, we will write
![]() $\left \{ Y_{i}\right \} \rightrightarrows X$
if there are specified congruences of each
$\left \{ Y_{i}\right \} \rightrightarrows X$
if there are specified congruences of each
![]() $Y_{i}$
into some X describing which points from the
$Y_{i}$
into some X describing which points from the
![]() $\left \{ Y_{i}\right \} $
are to be mapped to which points of
$\left \{ Y_{i}\right \} $
are to be mapped to which points of
![]() $X.$
Those specifications force congruences of various subsets of the various
$X.$
Those specifications force congruences of various subsets of the various
![]() $Y_{i}$
that are analogs to the rescaling statements for the subspaces
$Y_{i}$
that are analogs to the rescaling statements for the subspaces
![]() $J_{p,rs}$
in the previous paragraphs. We write
$J_{p,rs}$
in the previous paragraphs. We write
![]() $\left \{ Y_{i}\right \} \rightrightarrows \,??$
if we know the
$\left \{ Y_{i}\right \} \rightrightarrows \,??$
if we know the
![]() $\left \{ Y_{i}\right \} $
satisfy those congruences even if we do not know that there is an
$\left \{ Y_{i}\right \} $
satisfy those congruences even if we do not know that there is an
![]() $X.$
$X.$
We will pass freely between these ideas for RKHS and for sets in
![]() $\mathbb {CH}^{n}.$
$\mathbb {CH}^{n}.$
3.2 Equivalence of the two questions
Using Theorems 3.1 and 3.2, we can see that the two questions in the introduction are equivalent. Those theorems give us the following facts:
-
(1) Given a set of triangles
 $\left \{ Y_{i}\right \} _{i=1}^{4}$
in
$\left \{ Y_{i}\right \} _{i=1}^{4}$
in
 $\mathbb {CH}^{n}$
, there are three-dimensional
$\mathbb {CH}^{n}$
, there are three-dimensional
 $\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
such that (3.7)
$\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
such that (3.7) $$ \begin{align} J_{i}\sim DA(Y_{i}),\text{ }i=1,...,4. \end{align} $$
$$ \begin{align} J_{i}\sim DA(Y_{i}),\text{ }i=1,...,4. \end{align} $$
In the other direction, given three-dimensional
 $\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
, there are
$\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
, there are
 $\left \{ Y_{i}\right \} _{i=1}^{4}$
such that (3.7) holds. In either case, (3.7) continues to hold if the
$\left \{ Y_{i}\right \} _{i=1}^{4}$
such that (3.7) holds. In either case, (3.7) continues to hold if the
 $\left \{ J_{i}\right \} $
are replaced by rescalings
$\left \{ J_{i}\right \} $
are replaced by rescalings
 $\left \{ J_{i} ^{\prime }\right \} $
or if the
$\left \{ J_{i} ^{\prime }\right \} $
or if the
 $\left \{ Y_{i}\right \} $
are replaced by sets congruent to the
$\left \{ Y_{i}\right \} $
are replaced by sets congruent to the
 $\left \{ Y_{i}^{\prime }\right \} $
.
$\left \{ Y_{i}^{\prime }\right \} $
. -
(2) Given a tetrahedron X in
 $\mathbb {CH}^{n}$
, there is a four-dimensional
$\mathbb {CH}^{n}$
, there is a four-dimensional
 $H\in \mathcal {CPP}$
such that (3.8)
$H\in \mathcal {CPP}$
such that (3.8) $$ \begin{align} H\sim DA(X). \end{align} $$
$$ \begin{align} H\sim DA(X). \end{align} $$
In the other direction, given
 $H\in \mathcal {CPP}$
, there is an X such that (3.8) holds. In either case, (3.8) continues to hold if H is replaced by a rescaling
$H\in \mathcal {CPP}$
, there is an X such that (3.8) holds. In either case, (3.8) continues to hold if H is replaced by a rescaling
 $H^{\prime }$
or X is replaced by a congruent
$H^{\prime }$
or X is replaced by a congruent
 $X^{\prime }.$
$X^{\prime }.$
Hence, we have the following proposition.
Proposition 3.4 Given triangles
![]() $\left \{ Y_{i}\right \} _{i=1}^{4}$
in
$\left \{ Y_{i}\right \} _{i=1}^{4}$
in
![]() $\mathbb {CH}^{n}$
and Hilbert spaces
$\mathbb {CH}^{n}$
and Hilbert spaces
![]() $\left \{ J_{i}\right \} _{i=1} ^{4}\subset \mathcal {CPP}$
which are related as in (3.7), there is an X with
$\left \{ J_{i}\right \} _{i=1} ^{4}\subset \mathcal {CPP}$
which are related as in (3.7), there is an X with
![]() $\left \{ Y_{i}\right \} \rightrightarrows X$
if and only if there is an
$\left \{ Y_{i}\right \} \rightrightarrows X$
if and only if there is an
![]() $H\in \mathcal {CPP}$
with
$H\in \mathcal {CPP}$
with
![]() $\left \{ J_{i}\right \} \rightrightarrows H.$
In that case, H and X satisfy (3.8).
$\left \{ J_{i}\right \} \rightrightarrows H.$
In that case, H and X satisfy (3.8).
Proof This follows from statements (1) and (2) above together with the observation that for a finite
![]() $X\subset \mathbb {CH}^{n}$
, the regular subspaces of
$X\subset \mathbb {CH}^{n}$
, the regular subspaces of
![]() $DA(X)$
are exactly the spaces
$DA(X)$
are exactly the spaces
![]() $DA(Y)$
for Y a subset of
$DA(Y)$
for Y a subset of
![]() $X.$
$X.$
In the proposition, the assumption that (3.7) holds insures the
![]() $J_{i} \in \mathcal {CPP}$
. Even with that condition, having
$J_{i} \in \mathcal {CPP}$
. Even with that condition, having
![]() $H\in \mathcal {RK}$
and
$H\in \mathcal {RK}$
and
![]() $\left \{ J_{i}\right \} \rightrightarrows H$
is not enough to insure that
$\left \{ J_{i}\right \} \rightrightarrows H$
is not enough to insure that
![]() $H\in \mathcal {CPP}$
. This is shown by, for instance, Quiggin’s example which is discussed in Section 6.3.
$H\in \mathcal {CPP}$
. This is shown by, for instance, Quiggin’s example which is discussed in Section 6.3.
4 Geometry and
 $Kos$
$Kos$
We will use the functional
![]() $\operatorname *{kos}$
extensively below and so we pause now to develop the geometry associated with this functional.
$\operatorname *{kos}$
extensively below and so we pause now to develop the geometry associated with this functional.
4.1 Evaluating
 $Kos$
$Kos$
Because
![]() $\operatorname *{kos}$
is an automorphism invariant, we can study it for a general triple by first using an automorphism to place our triple in the configuration
$\operatorname *{kos}$
is an automorphism invariant, we can study it for a general triple by first using an automorphism to place our triple in the configuration
![]() $\Gamma $
described in (3.1):
$\Gamma $
described in (3.1):
![]() $\left \{ x_{1},x_{2} ,x_{3}\right \} =\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} $
. In that case, computing using (2.14) gives
$\left \{ x_{1},x_{2} ,x_{3}\right \} =\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} $
. In that case, computing using (2.14) gives
 $$ \begin{align} \operatorname*{kos}\nolimits_{1}(2,3)=\left\langle \left\langle \frac {(a,0)}{\left\Vert (a,0)\right\Vert },\frac{\left( x,b\right) }{\left\Vert \left( x,b\right) \right\Vert }\right\rangle \right\rangle =\frac{a\bar{x} }{\left\Vert x_{2}\right\Vert \left\Vert x_{3}\right\Vert }=\frac{\bar{x} }{\left\Vert x_{3}\right\Vert }=\frac{\left\vert \bar{x}\right\vert }{\left\Vert x_{3}\right\Vert }\frac{\bar{x}}{\left\vert \bar{x}\right\vert }. \end{align} $$
$$ \begin{align} \operatorname*{kos}\nolimits_{1}(2,3)=\left\langle \left\langle \frac {(a,0)}{\left\Vert (a,0)\right\Vert },\frac{\left( x,b\right) }{\left\Vert \left( x,b\right) \right\Vert }\right\rangle \right\rangle =\frac{a\bar{x} }{\left\Vert x_{2}\right\Vert \left\Vert x_{3}\right\Vert }=\frac{\bar{x} }{\left\Vert x_{3}\right\Vert }=\frac{\left\vert \bar{x}\right\vert }{\left\Vert x_{3}\right\Vert }\frac{\bar{x}}{\left\vert \bar{x}\right\vert }. \end{align} $$
To evaluate
![]() $\operatorname *{kos}\nolimits _{1}(2,3)$
for a general triple
$\operatorname *{kos}\nolimits _{1}(2,3)$
for a general triple
![]() $\left \{ x_{1},x_{2},x_{3}\right \} $
, we want a description that is invariant under automorphism of hyperbolic space and which gives the value in (4.1) for the particular triple
$\left \{ x_{1},x_{2},x_{3}\right \} $
, we want a description that is invariant under automorphism of hyperbolic space and which gives the value in (4.1) for the particular triple
![]() $\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} .$
Given the general triple, let
$\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} .$
Given the general triple, let
![]() $G(1,2)$
be the complex geodesic which contains
$G(1,2)$
be the complex geodesic which contains
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2} $
. Recall that
$x_{2} $
. Recall that
![]() $P_{G(1,2)}$
is the metric projection onto
$P_{G(1,2)}$
is the metric projection onto
![]() $G(1,2).$
$G(1,2).$
We will use the notion of angle between two geodesic segments in
![]() $G(1,2).$
Two geodesic segments in
$G(1,2).$
Two geodesic segments in
![]() $\mathbb {CH}^{n}$
form a bivalent vertex; however, there is not a natural notion of “vertex angle” which determines the shape of the vertex, rather the geometry of the vertex is determined by the complex number
$\mathbb {CH}^{n}$
form a bivalent vertex; however, there is not a natural notion of “vertex angle” which determines the shape of the vertex, rather the geometry of the vertex is determined by the complex number
![]() $\operatorname *{kos},$
this is discussed in Section 4.3. If, however, the two geodesics lie in the same complex geodesic, then there is a conformal map of that complex geodesic to the Poincare disk. In that case, we take the angle between the two segments to be the angle between their images in the Poincare geometry of the disk (which is in fact the same as the Euclidean angle).
$\operatorname *{kos},$
this is discussed in Section 4.3. If, however, the two geodesics lie in the same complex geodesic, then there is a conformal map of that complex geodesic to the Poincare disk. In that case, we take the angle between the two segments to be the angle between their images in the Poincare geometry of the disk (which is in fact the same as the Euclidean angle).
Here is the invariant statement we want.
Proposition 4.1 Set
![]() $P_{G(1,2)}x_{3}=y.$
Writing
$P_{G(1,2)}x_{3}=y.$
Writing
![]() $\operatorname *{kos} \nolimits _{x_{1}}(x_{2},x_{3})=re^{i\theta }$
,
$\operatorname *{kos} \nolimits _{x_{1}}(x_{2},x_{3})=re^{i\theta }$
,
![]() $r>0$
,
$r>0$
,
![]() $-\pi \leq \theta <\pi $
and
$-\pi \leq \theta <\pi $
and
![]() $\operatorname *{angle}$
for the hyperbolic angle, we have
$\operatorname *{angle}$
for the hyperbolic angle, we have
 $$ \begin{align} \!r & =\frac{\delta(x_{1},y)}{\delta(x_{1},x_{3})},\qquad\ \ \end{align} $$
$$ \begin{align} \!r & =\frac{\delta(x_{1},y)}{\delta(x_{1},x_{3})},\qquad\ \ \end{align} $$
Proof We need to show that the formula is correct for
![]() $\Gamma $
and that it is invariant. For
$\Gamma $
and that it is invariant. For
![]() $\Gamma $
, the complex geodesic
$\Gamma $
, the complex geodesic
![]() $G(1,2)$
is the unit disk in the first coordinate line, and in that case, it is elementary to show that the metric projection of
$G(1,2)$
is the unit disk in the first coordinate line, and in that case, it is elementary to show that the metric projection of
![]() $x_{3}$
onto
$x_{3}$
onto
![]() $G(1,2)$
is
$G(1,2)$
is
![]() $(x,0)$
. Also, for angles in the unit disk, the Euclidean angle and the hyperbolic angle are the same. These facts show that both (4.2) and (4.3) are correct for
$(x,0)$
. Also, for angles in the unit disk, the Euclidean angle and the hyperbolic angle are the same. These facts show that both (4.2) and (4.3) are correct for
![]() $\Gamma .$
$\Gamma .$
To see that (4.2) is invariant, note that the statement
![]() $P_{G(1,2)} x_{3}=y$
is invariant as is
$P_{G(1,2)} x_{3}=y$
is invariant as is
![]() $\delta .$
The equality (4.3) is more subtle because there is no natural definition of the angle of intersection for two geodesics in
$\delta .$
The equality (4.3) is more subtle because there is no natural definition of the angle of intersection for two geodesics in
![]() $\mathbb {CH}^{n}.$
However, the geodesic segments
$\mathbb {CH}^{n}.$
However, the geodesic segments
![]() $x_{1} P_{G(1,2)}x_{3}$
and
$x_{1} P_{G(1,2)}x_{3}$
and
![]() $x_{1}x_{2}$
are both in
$x_{1}x_{2}$
are both in
![]() $G(1,2).$
Any complex geodesic, in particular
$G(1,2).$
Any complex geodesic, in particular
![]() $G(1,2),$
is conformally equivalent to the classical Poincaré disk which does carry an invariant notion of angle between intersecting curves. Using that notion of angle, we see that (4.3) is also invariant.
$G(1,2),$
is conformally equivalent to the classical Poincaré disk which does carry an invariant notion of angle between intersecting curves. Using that notion of angle, we see that (4.3) is also invariant.
Given points
![]() $\left \{ x_{1},x_{2},x_{3}\right \} $
, we are using
$\left \{ x_{1},x_{2},x_{3}\right \} $
, we are using
![]() $\operatorname *{kos}$
to describe the geometry of the intersection of the geodesics
$\operatorname *{kos}$
to describe the geometry of the intersection of the geodesics
![]() $x_{1}x_{2}$
and
$x_{1}x_{2}$
and
![]() $x_{1}x_{3}.$
Other parameters can be used for the same purpose, for instance, in [Reference GoldmanGo, p. 88], Goldman uses angles,
$x_{1}x_{3}.$
Other parameters can be used for the same purpose, for instance, in [Reference GoldmanGo, p. 88], Goldman uses angles,
![]() $\phi ,\theta $
which satisfy
$\phi ,\theta $
which satisfy
![]() ${\cos \phi =\left \vert \operatorname *{kos} _{1}(2,3)\right \vert }$
and
${\cos \phi =\left \vert \operatorname *{kos} _{1}(2,3)\right \vert }$
and
![]() $\cos \theta =\operatorname {Re}\operatorname *{kos} _{1}(2,3)$
.
$\cos \theta =\operatorname {Re}\operatorname *{kos} _{1}(2,3)$
.
If the triangle is not in general position, we can say more about the relationship between the values of
![]() $\operatorname *{kos}$
at the vertices and the shape of the triangle. Given a triangle
$\operatorname *{kos}$
at the vertices and the shape of the triangle. Given a triangle
![]() $T=\left \{ x_{1},x_{2} ,x_{3}\right \} \subset \ \mathbb {CH}^{2}$
, we use an automorphism to suppose that
$T=\left \{ x_{1},x_{2} ,x_{3}\right \} \subset \ \mathbb {CH}^{2}$
, we use an automorphism to suppose that
![]() $x_{1}$
is at the origin. Regard
$x_{1}$
is at the origin. Regard
![]() $\mathbb {CH}^{2}$
as
$\mathbb {CH}^{2}$
as
![]() $\mathbb {B}_{2}$
inside
$\mathbb {B}_{2}$
inside
![]() $\mathbb {C}^{2},$
denote by V the real linear span of the points of
$\mathbb {C}^{2},$
denote by V the real linear span of the points of
![]() $T,$
and set
$T,$
and set
![]() $W=V\cap \mathbb {B}_{2}.$
It may be that W is a totally geodesic submanifold of
$W=V\cap \mathbb {B}_{2}.$
It may be that W is a totally geodesic submanifold of
![]() $\mathbb {CH}^{2}.$
In that case, with the origin in
$\mathbb {CH}^{2}.$
In that case, with the origin in
![]() $W,$
there are three possibilities. First, W may be a classical geodesic in which case it will be a line segment through the origin. Second, W may be a complex geodesic which contains the origin. In that case, we can suppose it is the unit disk in the plane of the first coordinate and hence it is the classical Poincaré disk with constant negative curvature
$W,$
there are three possibilities. First, W may be a classical geodesic in which case it will be a line segment through the origin. Second, W may be a complex geodesic which contains the origin. In that case, we can suppose it is the unit disk in the plane of the first coordinate and hence it is the classical Poincaré disk with constant negative curvature
![]() $-1$
. The final possibility is that W is a totally real totally geodesic disk and hence, after an automorphism, we can suppose it is
$-1$
. The final possibility is that W is a totally real totally geodesic disk and hence, after an automorphism, we can suppose it is
![]() ${RB_{2}=\left \{ \left ( r,s\right ) \in \mathbb {B}_{2}:r,s\in \mathbb {R}\right \},}$
the Beltrami-Klein disk of constant curvature
${RB_{2}=\left \{ \left ( r,s\right ) \in \mathbb {B}_{2}:r,s\in \mathbb {R}\right \},}$
the Beltrami-Klein disk of constant curvature
![]() $-1/4.$
$-1/4.$
In the first case, noting (4.2) and (4.3), we see that
![]() $\operatorname *{kos}\nolimits _{1}(2,3)=\pm 1.$
The value
$\operatorname *{kos}\nolimits _{1}(2,3)=\pm 1.$
The value
![]() $-1$
occurs when
$-1$
occurs when
![]() $x_{1}$
separates the other two points, the value
$x_{1}$
separates the other two points, the value
![]() $+1$
when it does not. In the second case,
$+1$
when it does not. In the second case,
![]() $x_{3}$
is in
$x_{3}$
is in
![]() $G(1,2)$
and so
$G(1,2)$
and so
![]() $P_{G(1,2)}x_{3}=x_{3}.$
From (4.2), we see that
$P_{G(1,2)}x_{3}=x_{3}.$
From (4.2), we see that
![]() $\left \vert \operatorname *{kos}\nolimits _{x_{1} }(x_{2},x_{3})\right \vert =1$
and then from (4.3) that
$\left \vert \operatorname *{kos}\nolimits _{x_{1} }(x_{2},x_{3})\right \vert =1$
and then from (4.3) that
![]() $\operatorname *{kos}\nolimits _{1}(2,3)=e^{-i\gamma }$
where
$\operatorname *{kos}\nolimits _{1}(2,3)=e^{-i\gamma }$
where
![]() $\gamma $
is the Euclidean angle between the segments
$\gamma $
is the Euclidean angle between the segments
![]() $x_{1}x_{2}$
and
$x_{1}x_{2}$
and
![]() $x_{1}x_{3}.$
Thus,
$x_{1}x_{3}.$
Thus,
![]() $\gamma $
is the Euclidean and also the hyperbolic angle at vertex
$\gamma $
is the Euclidean and also the hyperbolic angle at vertex
![]() $x_{1}.$
Similarly, the values of
$x_{1}.$
Similarly, the values of
![]() $\operatorname *{kos}$
at the other two vertices give the other angles. The congruence class of a triangle in a plane of constant negative curvature is determined by its angles and hence in this case also by the three values of
$\operatorname *{kos}$
at the other two vertices give the other angles. The congruence class of a triangle in a plane of constant negative curvature is determined by its angles and hence in this case also by the three values of
![]() $\operatorname *{kos}$
. Finally, in the third case, the triangle is in a totally real vector space and we are in the situation discussed in Proposition 6.7. By automorphism invariance, we may suppose
$\operatorname *{kos}$
. Finally, in the third case, the triangle is in a totally real vector space and we are in the situation discussed in Proposition 6.7. By automorphism invariance, we may suppose
![]() $x_{1}$
is at the origin. From (2.14), we see that
$x_{1}$
is at the origin. From (2.14), we see that
![]() $\operatorname *{kos}\nolimits _{x_{1}}(x_{2},x_{3})=\cos \theta $
where
$\operatorname *{kos}\nolimits _{x_{1}}(x_{2},x_{3})=\cos \theta $
where
![]() $\theta $
is the Euclidean angle of the vertex at the origin of the triangle with vertices
$\theta $
is the Euclidean angle of the vertex at the origin of the triangle with vertices
![]() $\left \{ x_{i}\right \} _{i=1}^{3}.$
However, the intersection of the real plane with those vertices with
$\left \{ x_{i}\right \} _{i=1}^{3}.$
However, the intersection of the real plane with those vertices with
![]() $\mathbb {CH}^{2}$
is the Beltrami–Klein model of
$\mathbb {CH}^{2}$
is the Beltrami–Klein model of
![]() $\mathbb {RH}^{2}$
which, at the origin, is conformal with the Euclidean geometry. Hence,
$\mathbb {RH}^{2}$
which, at the origin, is conformal with the Euclidean geometry. Hence,
![]() $\theta $
is also the angle at
$\theta $
is also the angle at
![]() $x_{1}$
of the hyperbolic triangle with vertices
$x_{1}$
of the hyperbolic triangle with vertices
![]() $\left \{ x_{i}\right \} _{i=1}^{3}$
sitting in a copy of
$\left \{ x_{i}\right \} _{i=1}^{3}$
sitting in a copy of
![]() $\mathbb {RH}^{2}.$
Similarly for the other two vertices. Hence, again, we know the three angles of a triangle in a plane of constant negative curvature and hence know its congruence class. Finally, looking backward, we see that the first case is the second and third cases holding simultaneously.
$\mathbb {RH}^{2}.$
Similarly for the other two vertices. Hence, again, we know the three angles of a triangle in a plane of constant negative curvature and hence know its congruence class. Finally, looking backward, we see that the first case is the second and third cases holding simultaneously.
In each of these cases, the argument can be reversed. If
![]() $\operatorname *{kos} \nolimits _{1}(2,3)=\pm 1$
, then W is a line through the origin, if
$\operatorname *{kos} \nolimits _{1}(2,3)=\pm 1$
, then W is a line through the origin, if
![]() $\left \vert \operatorname *{kos}\nolimits _{x_{1}}(x_{2},x_{3})\right \vert =1$
, then
$\left \vert \operatorname *{kos}\nolimits _{x_{1}}(x_{2},x_{3})\right \vert =1$
, then
![]() $P_{G(1,2)}x_{3}=x_{3}$
, and hence the triangle lies in a complex geodesic, and finally, again noting Proposition 6.6, if
$P_{G(1,2)}x_{3}=x_{3}$
, and hence the triangle lies in a complex geodesic, and finally, again noting Proposition 6.6, if
![]() $\operatorname *{kos} \nolimits _{x_{1}}(x_{2},x_{3})$
is real, then after automorphism, the triangle is in the position described.
$\operatorname *{kos} \nolimits _{x_{1}}(x_{2},x_{3})$
is real, then after automorphism, the triangle is in the position described.
4.2
 $Kos$
and other invariants
$Kos$
and other invariants
In Theorem 3.1, we recalled the result of Brehm [Reference BrehmBr] that equality of the data sets
![]() $S^{\prime }$
is a congruence criterion for triangles in
$S^{\prime }$
is a congruence criterion for triangles in
![]() $\mathbb {CH}^{n}$
. That criterion and variations are often used in describing the geometry of finite sets in
$\mathbb {CH}^{n}$
. That criterion and variations are often used in describing the geometry of finite sets in
![]() $\mathbb {CH}^{n}$
[Reference Brehm and Et-TaouiBE, Reference Cunha and GusevskiiCG, Reference Hakim and SandlerHS, Reference GusevskiiG, Reference RochbergRo]. Here, we mainly use the congruence criterion given by the dataset
$\mathbb {CH}^{n}$
[Reference Brehm and Et-TaouiBE, Reference Cunha and GusevskiiCG, Reference Hakim and SandlerHS, Reference GusevskiiG, Reference RochbergRo]. Here, we mainly use the congruence criterion given by the dataset
![]() $S^{\prime \prime }$
which is, as we noted in Remark 1, an analog of the classical side-angle-side congruence criterion for Euclidean triangles.
$S^{\prime \prime }$
which is, as we noted in Remark 1, an analog of the classical side-angle-side congruence criterion for Euclidean triangles.
It is straightforward to pass between
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S^{\prime \prime }.$
The parameters are invariant, so we can assume that we are in the model case and the triangle is
$S^{\prime \prime }.$
The parameters are invariant, so we can assume that we are in the model case and the triangle is
![]() $\Gamma =\left \{ x_{1},x_{2},x_{3}\right \} =\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} .$
First, suppose we have the data
$\Gamma =\left \{ x_{1},x_{2},x_{3}\right \} =\left \{ \left ( 0,0\right ) ,\left ( a,0\right ) ,\left ( x,b\right ) \right \} .$
First, suppose we have the data
![]() $S^{\prime \prime },$
that is,
$S^{\prime \prime },$
that is,
![]() $a=\delta (x_{1},x_{2}),$
$a=\delta (x_{1},x_{2}),$
![]() ${\omega =\delta (x_{1},x_{3}),}$
and
${\omega =\delta (x_{1},x_{3}),}$
and
![]() $\operatorname *{kos}\nolimits _{1}(2,3)$
are known. Using those values and (2.14), we also know
$\operatorname *{kos}\nolimits _{1}(2,3)$
are known. Using those values and (2.14), we also know
![]() $a\bar {x}$
. Hence, using (2.9), we can find the third side length using
$a\bar {x}$
. Hence, using (2.9), we can find the third side length using
 $$ \begin{align} \delta^{2}(x_{2},x_{3})=1-\frac{(1-\left\Vert x_{2}\right\Vert ^{2} )(1-\left\Vert x_{3}\right\Vert ^{2})}{\left\vert 1-\left\langle \left\langle x_{2},x_{3}\right\rangle \right\rangle \right\vert ^{2}}=1-\frac{(1-\alpha ^{2})(1-\omega^{2})}{\left\vert 1-\alpha\bar{x}\right\vert ^{2}}. \end{align} $$
$$ \begin{align} \delta^{2}(x_{2},x_{3})=1-\frac{(1-\left\Vert x_{2}\right\Vert ^{2} )(1-\left\Vert x_{3}\right\Vert ^{2})}{\left\vert 1-\left\langle \left\langle x_{2},x_{3}\right\rangle \right\rangle \right\vert ^{2}}=1-\frac{(1-\alpha ^{2})(1-\omega^{2})}{\left\vert 1-\alpha\bar{x}\right\vert ^{2}}. \end{align} $$
To finish determining
![]() $S^{\prime }$
, we need to find
$S^{\prime }$
, we need to find
![]() $\beta ,$
the angular invariant. For this triangle,
$\beta ,$
the angular invariant. For this triangle,
![]() $\beta =\arg (1-a\bar {x})$
, and, as we just mentioned,
$\beta =\arg (1-a\bar {x})$
, and, as we just mentioned,
![]() $a\bar {x}$
is known; hence,
$a\bar {x}$
is known; hence,
![]() $\beta $
is known.
$\beta $
is known.
In the other direction, to go from
![]() $S^{\prime }$
to
$S^{\prime }$
to
![]() $S^{\prime \prime }$
, we need to find
$S^{\prime \prime }$
, we need to find
![]() $\operatorname *{kos}_{1}(2,3).$
In this case, we know the three side lengths, and hence, noting (4.4), we know
$\operatorname *{kos}_{1}(2,3).$
In this case, we know the three side lengths, and hence, noting (4.4), we know
![]() $\left \vert 1-\alpha \bar {x}\right \vert .$
We also know the angular invariant
$\left \vert 1-\alpha \bar {x}\right \vert .$
We also know the angular invariant
![]() $\beta =\arg (1-a\bar {x}).$
Combining these two, we know
$\beta =\arg (1-a\bar {x}).$
Combining these two, we know
![]() $a\bar {x}.$
With that information, and using (4.1), we can find
$a\bar {x}.$
With that information, and using (4.1), we can find
![]() $\operatorname *{kos}_{1}(2,3).$
$\operatorname *{kos}_{1}(2,3).$
4.3
 $Kos$
and the geometry of vertices
$Kos$
and the geometry of vertices
For a bivalent vertex in
![]() $\mathbb {R}^{n}$
, the cosine of the vertex angle carries all the intrinsic geometric data about the vertex. The geometry of a trivalent vertex is determined by the geometry of the three component bivalent vertices. The values of
$\mathbb {R}^{n}$
, the cosine of the vertex angle carries all the intrinsic geometric data about the vertex. The geometry of a trivalent vertex is determined by the geometry of the three component bivalent vertices. The values of
![]() $\operatorname *{kos}$
provide similar information for vertices in
$\operatorname *{kos}$
provide similar information for vertices in
![]() $\mathbb {CH}^{n}.$
$\mathbb {CH}^{n}.$
To set the stage, we first consider sets in
![]() $\mathbb {R}^{n}$
. By a vertex
$\mathbb {R}^{n}$
. By a vertex
![]() $\mathbf {V}$
in
$\mathbf {V}$
in
![]() $\mathbb {R}^{n}$
, we mean a collection of two or more line segments, rays, with a common starting point the vertex point, or vertex, V. We call
$\mathbb {R}^{n}$
, we mean a collection of two or more line segments, rays, with a common starting point the vertex point, or vertex, V. We call
![]() $\mathbf {V}$
bivalent if it has two rays, trivalent if there are three, multivalent in general. We suppose the rays of a bivalent vertex are ordered. (That will be important in the complex case.) The two rays of a bivalent vertex span an affine plane and form an angle in that plane, the vertex angle. We say two vertices are (Euclidean) congruent if there is a Euclidean isometry placing the second vertex point at the same position as the first and so that the initial segments of the rays of the second vertex coincide with the initial segments of the rays of the first.
$\mathbf {V}$
bivalent if it has two rays, trivalent if there are three, multivalent in general. We suppose the rays of a bivalent vertex are ordered. (That will be important in the complex case.) The two rays of a bivalent vertex span an affine plane and form an angle in that plane, the vertex angle. We say two vertices are (Euclidean) congruent if there is a Euclidean isometry placing the second vertex point at the same position as the first and so that the initial segments of the rays of the second vertex coincide with the initial segments of the rays of the first.
Proposition 4.2 Two bivalent vertices in
![]() $\mathbb {R}^{n}$
are congruent if and only if the cosines of their vertex angles are equal.
$\mathbb {R}^{n}$
are congruent if and only if the cosines of their vertex angles are equal.
If three Euclidean triangles have pairs of matching side lengths, then they can be put together as faces of a tetrahedron if and only if the three dihedral angles that would be joined at a vertex can, in fact, be joined to form a trivalent vertex. (The simple classical condition for this is in Corollary 6.9.) In particular, there is no constraint on the side lengths beyond the matching condition. Here is a precise statement.
Suppose we are given
![]() $\mathfrak {S}$
, a set of three triangles
$\mathfrak {S}$
, a set of three triangles
![]() $\left \{ T_{i}\right \} _{i=1}^{3}$
each contained in some
$\left \{ T_{i}\right \} _{i=1}^{3}$
each contained in some
![]() $\mathbb {R}^{n}.$
Suppose for
$\mathbb {R}^{n}.$
Suppose for
![]() $i=1,2,3$
that
$i=1,2,3$
that
![]() $T_{i}$
has vertices
$T_{i}$
has vertices
![]() $\left \{ x_{i1},x_{ia},x_{ib} \right \} ,$
that the Euclidean length of the side
$\left \{ x_{i1},x_{ia},x_{ib} \right \} ,$
that the Euclidean length of the side
![]() $x_{i1}x_{ia}$
is
$x_{i1}x_{ia}$
is
![]() $l_{ia}$
and similarly for
$l_{ia}$
and similarly for
![]() $l_{ib}$
, and that
$l_{ib}$
, and that
![]() $\mathbf {W}_{i}$
is the bivalent vertex in
$\mathbf {W}_{i}$
is the bivalent vertex in
![]() $T_{i}$
with vertex point
$T_{i}$
with vertex point
![]() $x_{i1}$
and rays ordered similarly to the sides of the triangle;
$x_{i1}$
and rays ordered similarly to the sides of the triangle;
![]() $x_{i1}x_{ia}$
first,
$x_{i1}x_{ia}$
first,
![]() $x_{i1}x_{ib}$
second. It may or may not be possible to join these three triangles as faces of a tetrahedron in some
$x_{i1}x_{ib}$
second. It may or may not be possible to join these three triangles as faces of a tetrahedron in some
![]() $\mathbb {R}^{n}.$
That is there may be or may not be a tetrahedron
$\mathbb {R}^{n}.$
That is there may be or may not be a tetrahedron
![]() $\left \{ y_{1},y_{2},y_{3},y_{4}\right \} $
in some
$\left \{ y_{1},y_{2},y_{3},y_{4}\right \} $
in some
![]() $\mathbb {R}^{n}$
with the triangular face
$\mathbb {R}^{n}$
with the triangular face
![]() $\left \{ y_{1},y_{2},y_{3}\right \} $
congruent to
$\left \{ y_{1},y_{2},y_{3}\right \} $
congruent to
![]() $T_{1},$
$T_{1},$
![]() $\left \{ y_{1},y_{3},y_{4}\right \} $
congruent to
$\left \{ y_{1},y_{3},y_{4}\right \} $
congruent to
![]() $T_{2},$
and
$T_{2},$
and
![]() $\left \{ y_{1},y_{2},y_{4}\right \} $
congruent to the triangle
$\left \{ y_{1},y_{2},y_{4}\right \} $
congruent to the triangle
![]() ${\widetilde {T_{3}}=\left \{ x_{31},x_{3b},x_{3a}\right \} }$
. (The triangle
${\widetilde {T_{3}}=\left \{ x_{31},x_{3b},x_{3a}\right \} }$
. (The triangle
![]() $\widetilde {T_{3}}$
has the same vertices as
$\widetilde {T_{3}}$
has the same vertices as
![]() $T_{3}$
but in a different order.) Certainly, a necessary condition for building a tetrahedron is that certain side lengths match.
$T_{3}$
but in a different order.) Certainly, a necessary condition for building a tetrahedron is that certain side lengths match.
Definition 4.3 The set of three triangles
![]() $\mathfrak {S}$
is said to be a matched set if there are numbers
$\mathfrak {S}$
is said to be a matched set if there are numbers
![]() $\left \{ L_{i}\right \} _{i=1}^{3}$
such that
$\left \{ L_{i}\right \} _{i=1}^{3}$
such that
Proposition 4.4 Given a matched set of three Euclidean triangles
![]() $\mathfrak {S}$
, the following are equivalent.
$\mathfrak {S}$
, the following are equivalent.
-
(1) The triangles of
 $\mathfrak {S}$
are congruent to the three faces of a tetrahedron.
$\mathfrak {S}$
are congruent to the three faces of a tetrahedron. -
(2) If
 $\mathfrak {S}^{\prime }$
is another matched set of three triangles (with associated data denoted by primes) and for
$\mathfrak {S}^{\prime }$
is another matched set of three triangles (with associated data denoted by primes) and for
 $i=1,2,3$
the bivalent vertex
$i=1,2,3$
the bivalent vertex
 $\mathbf {W}_{i}^{\prime }$
is congruent to the bivalent vertex
$\mathbf {W}_{i}^{\prime }$
is congruent to the bivalent vertex
 $\mathbf {W}_{i}$
, then the triangles of
$\mathbf {W}_{i}$
, then the triangles of
 $\mathfrak {S}^{\prime }$
are congruent to the faces of a tetrahedron. That is, the previous conclusion holds for any choice of the lengths
$\mathfrak {S}^{\prime }$
are congruent to the faces of a tetrahedron. That is, the previous conclusion holds for any choice of the lengths
 $\{L_{i}^{^{\prime }}\}.$
$\{L_{i}^{^{\prime }}\}.$
-
(3) There is a trivalent vertex
 $\mathbf {V}$
whose three component bivalent vertices are congruent to the three bivalent vertices
$\mathbf {V}$
whose three component bivalent vertices are congruent to the three bivalent vertices
 $\left \{ \mathbf {W} _{i}\right \} _{i=1}^{3}.$
$\left \{ \mathbf {W} _{i}\right \} _{i=1}^{3}.$
In each case, the tetrahedron or the trivalent vertex is unique up to Euclidean congruence.
Proof That (2) implies (1) implies (3) is trivial. To finish, we show (3) implies (1). If (3) holds, we have a trivalent vertex
![]() $\mathbf {V.}$
Extend the three segments forming
$\mathbf {V.}$
Extend the three segments forming
![]() $\mathbf {V}$
to half lines starting at the vertex point. Select points on those three half lines so that their distances from the vertex point are the values
$\mathbf {V}$
to half lines starting at the vertex point. Select points on those three half lines so that their distances from the vertex point are the values
![]() $L_{i}^{\prime }$
from (2). Those three points together with the vertex point give the four vertices of the desired tetrahedron. By construction, the side lengths meeting at the vertex point are correct. The congruence of the triangular faces meeting at that point to the target triangles is a consequence in each case of congruence of triangles with a pair of matching side lengths and equality of the included angel. The side lengths match by construction, and the angles are equal by the hypotheses in (3) on the bivalent vertices which form the given trivalent vertex.
$L_{i}^{\prime }$
from (2). Those three points together with the vertex point give the four vertices of the desired tetrahedron. By construction, the side lengths meeting at the vertex point are correct. The congruence of the triangular faces meeting at that point to the target triangles is a consequence in each case of congruence of triangles with a pair of matching side lengths and equality of the included angel. The side lengths match by construction, and the angles are equal by the hypotheses in (3) on the bivalent vertices which form the given trivalent vertex.
We now prove analogs of the two previous propositions for
![]() $\mathbb {CH}^{n}.$
By a vertex
$\mathbb {CH}^{n}.$
By a vertex
![]() $\mathbf {V}$
in
$\mathbf {V}$
in
![]() $\mathbb {CH}^{n}$
, we mean a collection of two or more geodesic segments, rays,
$\mathbb {CH}^{n}$
, we mean a collection of two or more geodesic segments, rays,
![]() $R_{i},$
with a common starting point the vertex point,
$R_{i},$
with a common starting point the vertex point,
![]() $V.$
Again, a vertex may be bivalent, trivalent, or multivalent. We say two vertices are congruent if there is an automorphism placing the second vertex point on the first and so that initial segments of the two sets of rays overlap.
$V.$
Again, a vertex may be bivalent, trivalent, or multivalent. We say two vertices are congruent if there is an automorphism placing the second vertex point on the first and so that initial segments of the two sets of rays overlap.
The geometry of a bivalent vertex in
![]() $\mathbb {CH}^{n}$
can be described by two real numbers or one complex number. We will use the complex quantity
$\mathbb {CH}^{n}$
can be described by two real numbers or one complex number. We will use the complex quantity
![]() $\operatorname *{kos}\left ( \mathbf {V}\right ) $
which we define to be
$\operatorname *{kos}\left ( \mathbf {V}\right ) $
which we define to be
![]() $\operatorname *{kos}_{V}(x_{1},x_{2})$
where V is the vertex point and
$\operatorname *{kos}_{V}(x_{1},x_{2})$
where V is the vertex point and
![]() $x_{i}$
is chosen on the ray
$x_{i}$
is chosen on the ray
![]() $R_{i}$
,
$R_{i}$
,
![]() $i=1,2.$
The formula (2.14) shows that this value does not depend on those choices. Thus, if
$i=1,2.$
The formula (2.14) shows that this value does not depend on those choices. Thus, if
![]() $\left \{ x_{1},x_{2},x_{3}\right \} $
is a triangle and
$\left \{ x_{1},x_{2},x_{3}\right \} $
is a triangle and
![]() $\mathbf {V}$
the bivalent vertex with vertex point
$\mathbf {V}$
the bivalent vertex with vertex point
![]() $x_{1}$
, then
$x_{1}$
, then
![]() ${\operatorname *{kos}\left ( \mathbf {V}\right ) =\operatorname *{kos}_{1}(2,3)}$
.
${\operatorname *{kos}\left ( \mathbf {V}\right ) =\operatorname *{kos}_{1}(2,3)}$
.
Proposition 4.5 Two bivalent vertices,
![]() $\mathbf {V}$
,
$\mathbf {V}$
,
![]() $\mathbf {W,}$
in
$\mathbf {W,}$
in
![]() $\mathbb {CH}^{n}$
are congruent if and only if
$\mathbb {CH}^{n}$
are congruent if and only if
![]() $\operatorname *{kos}\left ( \mathbf {V}\right ) =\operatorname *{kos}\left ( \mathbf {W}\right ).$
$\operatorname *{kos}\left ( \mathbf {V}\right ) =\operatorname *{kos}\left ( \mathbf {W}\right ).$
Proof If the vertices are congruent, then the conclusion is clear. In the other direction, let v be the vertex point of
![]() $\mathbf {V,}$
pick
$\mathbf {V,}$
pick
![]() $\varepsilon $
small, and pick x and y on the two rays of
$\varepsilon $
small, and pick x and y on the two rays of
![]() $\mathbf {V}$
at distance
$\mathbf {V}$
at distance
![]() $\varepsilon $
from
$\varepsilon $
from
![]() $v.$
Let w be the vertex point
$v.$
Let w be the vertex point
![]() $\mathbf {W}$
and pick points
$\mathbf {W}$
and pick points
![]() $r,s$
on the rays forming
$r,s$
on the rays forming
![]() $\mathbf {W}$
at distance
$\mathbf {W}$
at distance
![]() $\varepsilon $
from
$\varepsilon $
from
![]() $w.$
The triangles
$w.$
The triangles
![]() $\left \{ v,x,y\right \} $
and
$\left \{ v,x,y\right \} $
and
![]() $\left \{ w,r,s\right \} $
give the same values for (3.3), the dataset
$\left \{ w,r,s\right \} $
give the same values for (3.3), the dataset
![]() $S^{\prime \prime }$
of Theorem 3.1, and hence, by that theorem, they are congruent. That congruence of triangles also gives the required congruence of the vertices.
$S^{\prime \prime }$
of Theorem 3.1, and hence, by that theorem, they are congruent. That congruence of triangles also gives the required congruence of the vertices.
There is a contrast between the real and complex cases. For a bivalent vertex
![]() $\mathbf {V}$
, let
$\mathbf {V}$
, let
![]() $\mathbf {V}_{\texttt {rev}}$
be the vertex obtained from
$\mathbf {V}_{\texttt {rev}}$
be the vertex obtained from
![]() $\mathbf {V}$
by reversing the order of the two rays. For vertices in
$\mathbf {V}$
by reversing the order of the two rays. For vertices in
![]() $\mathbb {RH}^{n}$
,
$\mathbb {RH}^{n}$
,
![]() $\mathbf {V}_{\texttt {rev}}$
is congruent to V. However, if
$\mathbf {V}_{\texttt {rev}}$
is congruent to V. However, if
![]() $\mathbf {V\subset } \ \mathbb {CH}^{n}$
, then
$\mathbf {V\subset } \ \mathbb {CH}^{n}$
, then
![]() $\mathbf {V} _{\texttt {rev}}$
is generically not congruent to
$\mathbf {V} _{\texttt {rev}}$
is generically not congruent to
![]() $\mathbf {V,}$
and it is congruent to
$\mathbf {V,}$
and it is congruent to
![]() $\mathbf {V}^{\ast },$
the vertex obtained by conjugating the coordinates of
$\mathbf {V}^{\ast },$
the vertex obtained by conjugating the coordinates of
![]() $\mathbf {V.}$
This can be seen by computing that
$\mathbf {V.}$
This can be seen by computing that
![]() $\operatorname *{kos} (\mathbf {V}_{\texttt {rev}}\mathbf {)}=\overline {\operatorname *{kos}\left ( \mathbf {V}\right ) }= \ \operatorname *{kos}(\mathbf {V}^{\ast }\mathbf {)}$
.
$\operatorname *{kos} (\mathbf {V}_{\texttt {rev}}\mathbf {)}=\overline {\operatorname *{kos}\left ( \mathbf {V}\right ) }= \ \operatorname *{kos}(\mathbf {V}^{\ast }\mathbf {)}$
.
Now, suppose we are given
![]() $\mathfrak {S,}$
a set of three triangles each in
$\mathfrak {S,}$
a set of three triangles each in
![]() $\mathbb {CH}^{n}$
. We continue the earlier notation and terminology, but now we use the pseudohyperbolic side lengths
$\mathbb {CH}^{n}$
. We continue the earlier notation and terminology, but now we use the pseudohyperbolic side lengths
![]() $\delta (\cdot ,\cdot )$
. With that change, the analog of Proposition 4.4 holds.
$\delta (\cdot ,\cdot )$
. With that change, the analog of Proposition 4.4 holds.
Proposition 4.6 Given a matched set of triangles
![]() $\mathfrak {S}$
in
$\mathfrak {S}$
in
![]() $\mathbb {CH}^{n}$
, the statements (1)–(3) of Proposition 4.4 are equivalent. If the conditions hold, then the congruence class of the tetrahedra and of the trivalent vertex are uniquely determined. In particular, the congruence class of three faces of a tetrahedron together with the congruence class of the vertex at which they meet determines the congruence class of the fourth face.
$\mathbb {CH}^{n}$
, the statements (1)–(3) of Proposition 4.4 are equivalent. If the conditions hold, then the congruence class of the tetrahedra and of the trivalent vertex are uniquely determined. In particular, the congruence class of three faces of a tetrahedron together with the congruence class of the vertex at which they meet determines the congruence class of the fourth face.
Proof It is immediate that
![]() $(2)\Longrightarrow (1)\Longrightarrow (3).$
To see that
$(2)\Longrightarrow (1)\Longrightarrow (3).$
To see that
![]() $(1)\Longrightarrow (2)$
, suppose from
$(1)\Longrightarrow (2)$
, suppose from
![]() $(1)$
that we have
$(1)$
that we have
![]() $\mathfrak {S}$
and the associated tetrahedron
$\mathfrak {S}$
and the associated tetrahedron
![]() $\Lambda $
and that we are given a new set of lengths
$\Lambda $
and that we are given a new set of lengths
![]() $\{L_{i}^{^{\prime }}\}$
from
$\{L_{i}^{^{\prime }}\}$
from
![]() $(2).$
Use an automorphism to replace
$(2).$
Use an automorphism to replace
![]() $\Lambda $
with the tetrahedron
$\Lambda $
with the tetrahedron
![]() $\Delta $
with coordinates given by (3.2). For
$\Delta $
with coordinates given by (3.2). For
![]() $i=2,3,4$
, select
$i=2,3,4$
, select
![]() $\gamma _{i}>0$
so that the tetrahedron
$\gamma _{i}>0$
so that the tetrahedron
![]() $\Delta ^{\prime }=\{x_{1},\gamma _{2}x_{2},\gamma _{3}x_{3},\gamma _{4}x_{4}\}$
has
$\Delta ^{\prime }=\{x_{1},\gamma _{2}x_{2},\gamma _{3}x_{3},\gamma _{4}x_{4}\}$
has
![]() $\left \Vert \gamma _{i}x_{i}\right \Vert =L_{i}^{\prime }$
. The bivalent vertices of
$\left \Vert \gamma _{i}x_{i}\right \Vert =L_{i}^{\prime }$
. The bivalent vertices of
![]() $\Delta ^{\prime }$
at the origin are obtained from those of
$\Delta ^{\prime }$
at the origin are obtained from those of
![]() $\Delta $
by changing the lengths of the rays which does not change the congruence class of the vertices. Hence, those vertices have the desired congruence classes. Also, the lengths of the edges of
$\Delta $
by changing the lengths of the rays which does not change the congruence class of the vertices. Hence, those vertices have the desired congruence classes. Also, the lengths of the edges of
![]() $\Delta ^{\prime }$
which meet at the origin match the
$\Delta ^{\prime }$
which meet at the origin match the
![]() $\left \{ L_{i}^{\prime }\right \} .$
Thus, by the results on
$\left \{ L_{i}^{\prime }\right \} .$
Thus, by the results on
![]() $S^{\prime \prime }$
in Theorem 3.1, the triangles of
$S^{\prime \prime }$
in Theorem 3.1, the triangles of
![]() $\mathfrak {S}^{\prime }$
are congruent to the faces of
$\mathfrak {S}^{\prime }$
are congruent to the faces of
![]() $\Delta ^{\prime },$
establishing
$\Delta ^{\prime },$
establishing
![]() $(2).$
To show that
$(2).$
To show that
![]() $(3)\Longrightarrow (1)$
, first use an automorphism to place the trivalent vertex
$(3)\Longrightarrow (1)$
, first use an automorphism to place the trivalent vertex
![]() $\mathbf {V}$
at the origin with its rays in the directions of the rays of
$\mathbf {V}$
at the origin with its rays in the directions of the rays of
![]() $\Delta $
of (3.2). Next, select a point on each ray whose distance from the origin is the appropriate
$\Delta $
of (3.2). Next, select a point on each ray whose distance from the origin is the appropriate
![]() $L_{i}.$
The triangles with vertex at the origin are, again by Theorem 3.1, congruent to the triangles of
$L_{i}.$
The triangles with vertex at the origin are, again by Theorem 3.1, congruent to the triangles of
![]() $\mathfrak {S}$
and hence the origin together with those three new points are the vertices of the tetrahedron required to show that (1) holds.
$\mathfrak {S}$
and hence the origin together with those three new points are the vertices of the tetrahedron required to show that (1) holds.
For uniqueness, first consider two trivalent vertices
![]() $\mathbf {W}$
and
$\mathbf {W}$
and
![]() $\mathbf {W}^{\prime }$
which satisfy condition (3). Pick a small
$\mathbf {W}^{\prime }$
which satisfy condition (3). Pick a small
![]() $\varepsilon $
and pick a point on each ray at distance
$\varepsilon $
and pick a point on each ray at distance
![]() $\varepsilon $
from the vertex. Let
$\varepsilon $
from the vertex. Let
![]() $\Sigma $
be the tetrahedron determined by those four points, and let
$\Sigma $
be the tetrahedron determined by those four points, and let
![]() $\Sigma ^{\prime }$
be the similar tetrahedron constructed using
$\Sigma ^{\prime }$
be the similar tetrahedron constructed using
![]() $\mathbf {W} ^{\prime }.$
We will be done if we show that
$\mathbf {W} ^{\prime }.$
We will be done if we show that
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma ^{\prime }$
are congruent. The argument which shows they are congruent also gives the uniqueness in statements (1) and (2). First, note that the results on
$\Sigma ^{\prime }$
are congruent. The argument which shows they are congruent also gives the uniqueness in statements (1) and (2). First, note that the results on
![]() $S^{\prime \prime }$
in Theorem 3.1 insures that the triangular faces of
$S^{\prime \prime }$
in Theorem 3.1 insures that the triangular faces of
![]() $\Sigma $
meeting at the vertex point
$\Sigma $
meeting at the vertex point
![]() $\mathbf {W}$
are congruent to those in
$\mathbf {W}$
are congruent to those in
![]() $\Sigma ^{\prime }$
meeting at the vertex point of
$\Sigma ^{\prime }$
meeting at the vertex point of
![]() $\mathbf {W}^{\prime }.$
By condition (5) of Theorem 3.2, this is enough to show that the tetrahedra are congruent.
$\mathbf {W}^{\prime }.$
By condition (5) of Theorem 3.2, this is enough to show that the tetrahedra are congruent.
In particular, note that in both the real and complex cases, the congruence class is completely described by the shapes of three faces and the geometry of the vertex where they meet. There need not be any mention of the geometry of the fourth face.
The analogous congruence result for multivalent vertices in
![]() $\mathbb {CH}^{n}$
is given in Corollary 5.3.
$\mathbb {CH}^{n}$
is given in Corollary 5.3.
4.4
 $Kos$
and area
$Kos$
and area
There is not a natural notion of area for a general triangle T in
![]() $\mathbb {CH}^{m}$
; however, there is a related invariant, the symplectic area of
$\mathbb {CH}^{m}$
; however, there is a related invariant, the symplectic area of
![]() $T,$
obtained by integrating the symplectic form of
$T,$
obtained by integrating the symplectic form of
![]() $\mathbb {CH}^{n}$
over a real two manifold bounded by the sides of
$\mathbb {CH}^{n}$
over a real two manifold bounded by the sides of
![]() $T.$
$T.$
However, if T sits inside a complex geodesic
![]() $A\subset \mathbb {CH}^{m}$
, then we can define and compute its area as follows. After an automorphism, we can suppose T is inside a copy of
$A\subset \mathbb {CH}^{m}$
, then we can define and compute its area as follows. After an automorphism, we can suppose T is inside a copy of
![]() $\mathbb {CH}^{1}$
inside
$\mathbb {CH}^{1}$
inside
![]() $\mathbb {CH}^{n}.$
That copy of
$\mathbb {CH}^{n}.$
That copy of
![]() $\mathbb {CH}^{1}$
is isometric to the classical Poincare disk of curvature
$\mathbb {CH}^{1}$
is isometric to the classical Poincare disk of curvature
![]() $-1.$
We define the area of T,
$-1.$
We define the area of T,
![]() $\operatorname *{Area}(T),$
to br the area of that copy of T in the Poincare disk. This definition is an automorphism invariant, and it can be shown that
$\operatorname *{Area}(T),$
to br the area of that copy of T in the Poincare disk. This definition is an automorphism invariant, and it can be shown that
![]() $\operatorname *{Area}(T)$
equals both the symplectic area of T and is also twice the angular invariant,
$\operatorname *{Area}(T)$
equals both the symplectic area of T and is also twice the angular invariant,
![]() $\alpha ,$
of T (defined in Section 2.3) [Reference GoldmanGo, Reference Hangan and MasalaHM].
$\alpha ,$
of T (defined in Section 2.3) [Reference GoldmanGo, Reference Hangan and MasalaHM].
We can also evaluate
![]() $\operatorname *{Area}(T)$
using
$\operatorname *{Area}(T)$
using
![]() $\operatorname *{kos}.$
$\operatorname *{kos}.$
Proposition 4.7 If
![]() $T=\left \{ x_{1},x_{2},x_{3}\right \} $
is a triangle in
$T=\left \{ x_{1},x_{2},x_{3}\right \} $
is a triangle in
![]() $\mathbb {CH}^{n}$
which sits inside a complex geodesic, then
$\mathbb {CH}^{n}$
which sits inside a complex geodesic, then
Proof After an automorphism of
![]() $\mathbb {CH}^{n}$
, we suppose that T is in the unit disk of
$\mathbb {CH}^{n}$
, we suppose that T is in the unit disk of
![]() $\mathbb {C}$
which we identify with
$\mathbb {C}$
which we identify with
![]() $\mathbb {CH}^{1}.$
From (2.13), we see that
$\mathbb {CH}^{1}.$
From (2.13), we see that
![]() $\operatorname *{kos}_{1}(2,3)$
is a positive multiple of
$\operatorname *{kos}_{1}(2,3)$
is a positive multiple of
Hence, in computing the left-hand side,
![]() $LHS$
, of (4.6), we can replace
$LHS$
, of (4.6), we can replace
![]() $\operatorname *{kos}(2,3)$
with
$\operatorname *{kos}(2,3)$
with
![]() $\kappa _{123}$
and similarly for other indices. The conformal involutions of the disk are given by Blaschke factors. Hence, noting that for
$\kappa _{123}$
and similarly for other indices. The conformal involutions of the disk are given by Blaschke factors. Hence, noting that for
![]() $a,b$
in the disk
$a,b$
in the disk
![]() $\left \langle \left \langle a,b\right \rangle \right \rangle =a\bar {b}$
, we find that
$\left \langle \left \langle a,b\right \rangle \right \rangle =a\bar {b}$
, we find that
![]() $\kappa _{123} =\frac {x_{1}-x_{2}}{1-x_{1}\overline {x_{2}}}\overline {\frac {x_{1}-x_{3} }{1-x_{1}\overline {x_{3}}}}.$
Thus,
$\kappa _{123} =\frac {x_{1}-x_{2}}{1-x_{1}\overline {x_{2}}}\overline {\frac {x_{1}-x_{3} }{1-x_{1}\overline {x_{3}}}}.$
Thus,
 $$\begin{align*}LHS=\pi-\arg\frac{-\Pi\left\vert x_{i}-x_{j}\right\vert ^{2}}{\Pi\left( 1-x_{i}\overline{x_{j}}\right) ^{2}} \end{align*}$$
$$\begin{align*}LHS=\pi-\arg\frac{-\Pi\left\vert x_{i}-x_{j}\right\vert ^{2}}{\Pi\left( 1-x_{i}\overline{x_{j}}\right) ^{2}} \end{align*}$$
with both products over the index pairs
![]() $\left \{ \left ( 1,2\right ) ,\left ( 2,3\right ) ,\left ( 3,1\right ) \right \} .$
The positive factor
$\left \{ \left ( 1,2\right ) ,\left ( 2,3\right ) ,\left ( 3,1\right ) \right \} .$
The positive factor
![]() $\Pi \left \vert x_{i}-x_{j}\right \vert ^{2}$
does not affect the value of
$\Pi \left \vert x_{i}-x_{j}\right \vert ^{2}$
does not affect the value of
![]() $\arg $
, and hence we continue with
$\arg $
, and hence we continue with
the last equality by (2.10).
To finish, we need to know that
![]() $2\alpha = \ \operatorname *{Area}(T).$
That is in [Reference GoldmanGo]. Alternatively, going back to (4.6), let
$2\alpha = \ \operatorname *{Area}(T).$
That is in [Reference GoldmanGo]. Alternatively, going back to (4.6), let
![]() $\gamma _{i}$
be the angle at vertex
$\gamma _{i}$
be the angle at vertex
![]() $x_{i}$
. Because
$x_{i}$
. Because
![]() $T\subset \mathbb {CH}^{1}$
, we see from Proposition 4.1 that
$T\subset \mathbb {CH}^{1}$
, we see from Proposition 4.1 that
![]() $\operatorname *{kos}_{1}(2,3)=e^{i\gamma _{1}}$
where
$\operatorname *{kos}_{1}(2,3)=e^{i\gamma _{1}}$
where
![]() $\gamma _{1}$
is the angle at
$\gamma _{1}$
is the angle at
![]() $x_{1}$
of the triangle
$x_{1}$
of the triangle
![]() $T.$
Similarly for the other indices. Using that, we see that
$T.$
Similarly for the other indices. Using that, we see that
![]() $LHS$
in (4.6) equals
$LHS$
in (4.6) equals
![]() $\pi -(\gamma _{1}+ \gamma _{2}+\gamma _{3})$
, which equals
$\pi -(\gamma _{1}+ \gamma _{2}+\gamma _{3})$
, which equals
![]() $\operatorname *{Area} (T)$
by the classical result based on the Gauss–Bonnet theorem
$\operatorname *{Area} (T)$
by the classical result based on the Gauss–Bonnet theorem
![]() $.$
$.$
In contrast to T, consider now a triangle R that sits inside a totally real submanifold M. (If M exists, it can be taken to have real dimension
![]() $2$
.) The previous discussion does not apply, and, in fact, the symplectic area of R is
$2$
.) The previous discussion does not apply, and, in fact, the symplectic area of R is
![]() $0.$
However, we have the following observation. We can suppose M is two-dimensional, and using a conformal automorphism, we can move M to
$0.$
However, we have the following observation. We can suppose M is two-dimensional, and using a conformal automorphism, we can move M to
![]() $RB_{2}=\left \{ \left ( x,y,0,...,0\right ) \in \mathbb {B}_{n}:x,y\in \mathbb {R}\right \} $
inside
$RB_{2}=\left \{ \left ( x,y,0,...,0\right ) \in \mathbb {B}_{n}:x,y\in \mathbb {R}\right \} $
inside
![]() $\mathbb {CH}^{n}=\mathbb {B}_{n}.$
That subspace of complex hyperbolic space is, isometrically, a copy of the Beltrami–Klein model of
$\mathbb {CH}^{n}=\mathbb {B}_{n}.$
That subspace of complex hyperbolic space is, isometrically, a copy of the Beltrami–Klein model of
![]() $\mathbb {RH}^{2}$
which has constant curvature
$\mathbb {RH}^{2}$
which has constant curvature
![]() $-1/4.$
As such, it carries a natural area measure, and we let
$-1/4.$
As such, it carries a natural area measure, and we let
![]() $\mathit {Area}(R)$
denote the area of R as a triangle in that space. This quantity is also invariant under conformal automorphisms of
$\mathit {Area}(R)$
denote the area of R as a triangle in that space. This quantity is also invariant under conformal automorphisms of
![]() $\mathbb {CH}^{n}.$
$\mathbb {CH}^{n}.$
Proposition 4.8 Suppose
![]() $R=\left \{ x_{1},x_{2},x_{3}\right \} $
sits in a totally real totally geodesic submanifold of
$R=\left \{ x_{1},x_{2},x_{3}\right \} $
sits in a totally real totally geodesic submanifold of
![]() $\mathbb {CH}^{n}.$
Then
$\mathbb {CH}^{n}.$
Then
Proof Without loss of generality,
![]() $M=RB_{2}$
. The equality is a consequence of two facts. First, taking note of (2.14),
$M=RB_{2}$
. The equality is a consequence of two facts. First, taking note of (2.14),
![]() $\cos ^{-1}\operatorname *{kos} (2,3)$
is the angle between the geodesics
$\cos ^{-1}\operatorname *{kos} (2,3)$
is the angle between the geodesics
![]() $x_{1}x_{2}$
and
$x_{1}x_{2}$
and
![]() $x_{1}x_{3},$
and similarly for the other indices. Second, by the Gauss–Bonnet theorem, the area of a triangle with angles
$x_{1}x_{3},$
and similarly for the other indices. Second, by the Gauss–Bonnet theorem, the area of a triangle with angles
![]() $\alpha ,\beta ,\gamma $
in a plane of constant curvature
$\alpha ,\beta ,\gamma $
in a plane of constant curvature
![]() $-1/4$
is
$-1/4$
is
![]() $4(\pi -(\alpha +\beta +\gamma )).$
$4(\pi -(\alpha +\beta +\gamma )).$
One proposition gives a result involving a sum of values of
![]() $\arg \operatorname *{kos}$
and the other a sum of values of
$\arg \operatorname *{kos}$
and the other a sum of values of
![]() $\cos ^{-1} \operatorname *{kos}.$
It would be interesting to have a general result which unifies the two.
$\cos ^{-1} \operatorname *{kos}.$
It would be interesting to have a general result which unifies the two.
5 Finite sets in
 $\mathbb {CH}^{n}$
$\mathbb {CH}^{n}$
5.1 Describing sets by their triangles
In Theorem 3.2, we saw that the congruence class of a finite
![]() $X\subset \mathbb {CH}^{n}$
is determined by the congruence classes of those of its subtriangles which share a specified designated vertex. From Theorem 3.1, we know that the congruence class of each of those triangles can be described using side lengths and the angular invariant. Those parameters have been used in describing the congruence class of finite
$X\subset \mathbb {CH}^{n}$
is determined by the congruence classes of those of its subtriangles which share a specified designated vertex. From Theorem 3.1, we know that the congruence class of each of those triangles can be described using side lengths and the angular invariant. Those parameters have been used in describing the congruence class of finite
![]() $X\subset \mathbb {CH}^{n}$
[Reference Brehm and Et-TaouiBE, Reference Cunha and GusevskiiCG, Reference GusevskiiG, Reference Hakim and SandlerHS, Reference RochbergRo] and have also been used for more general geometric questions, [Reference ClercC, CG]. When those parameters are restricted to sets in real hyperbolic space, the angular invariant trivializes leading to descriptions of polyhedra in
$X\subset \mathbb {CH}^{n}$
[Reference Brehm and Et-TaouiBE, Reference Cunha and GusevskiiCG, Reference GusevskiiG, Reference Hakim and SandlerHS, Reference RochbergRo] and have also been used for more general geometric questions, [Reference ClercC, CG]. When those parameters are restricted to sets in real hyperbolic space, the angular invariant trivializes leading to descriptions of polyhedra in
![]() $\mathbb {RH}^{n}$
in terms of edge lengths.
$\mathbb {RH}^{n}$
in terms of edge lengths.
Here, instead of side lengths and the angular invariant, we use side lengths and
![]() $\operatorname *{kos}$
to describe the constituent triangles of
$\operatorname *{kos}$
to describe the constituent triangles of
![]() $X.$
This alternative description emphasizes a different type of geometric data. For instance, when restricted to sets in real hyperbolic space, it produces a description of polyhedra using side lengths and vertex angles. The parameters only have natural geometric constraints, and their values interact well with passage to subsets. That lets us give explicit answers to the questions in the introduction.
$X.$
This alternative description emphasizes a different type of geometric data. For instance, when restricted to sets in real hyperbolic space, it produces a description of polyhedra using side lengths and vertex angles. The parameters only have natural geometric constraints, and their values interact well with passage to subsets. That lets us give explicit answers to the questions in the introduction.
Suppose we are given
![]() $X=\left \{ x_{i}\right \} _{i=1}^{n+1} \ \subset \mathbb {CH}^{n}$
. If we connect
$X=\left \{ x_{i}\right \} _{i=1}^{n+1} \ \subset \mathbb {CH}^{n}$
. If we connect
![]() $x_{1}$
to each of the other
$x_{1}$
to each of the other
![]() $x_{i}$
by a geodesic
$x_{i}$
by a geodesic
![]() $\gamma _{1i}$
, then the point
$\gamma _{1i}$
, then the point
![]() $x_{1}$
will be the vertex point of an n-valent vertex
$x_{1}$
will be the vertex point of an n-valent vertex
![]() $\mathbf {V}$
which is composed of the bivalent vertices
$\mathbf {V}$
which is composed of the bivalent vertices
![]() $\mathbf {V}_{ij}$
,
$\mathbf {V}_{ij}$
,
![]() $2\leq i,j\leq n+1$
having
$2\leq i,j\leq n+1$
having
![]() $\gamma _{1i}$
as a first ray and
$\gamma _{1i}$
as a first ray and
![]() $\gamma _{1j}$
as a second. We can describe X using the distances between
$\gamma _{1j}$
as a second. We can describe X using the distances between
![]() $x_{1}$
and the other
$x_{1}$
and the other
![]() $x_{j}$
and the numbers
$x_{j}$
and the numbers
![]() $K_{ij} =\operatorname *{kos}(\mathbf {V}_{ij})$
. Specifically, recalling the definition (2.15), we define the n-vector
$K_{ij} =\operatorname *{kos}(\mathbf {V}_{ij})$
. Specifically, recalling the definition (2.15), we define the n-vector
![]() $\rho (X)$
and the
$\rho (X)$
and the
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $\mathcal {M}(X)$
by
$\mathcal {M}(X)$
by
The functionals that give the entries of the vector
![]() $\rho $
and the matrix
$\rho $
and the matrix
![]() $\mathcal {M}$
are defined for any
$\mathcal {M}$
are defined for any
![]() $H\in \mathcal {RK}$
, and hence those same definitions can be used to produce
$H\in \mathcal {RK}$
, and hence those same definitions can be used to produce
![]() $\rho (H)$
and
$\rho (H)$
and
![]() $\mathcal {M}(H)$
.
$\mathcal {M}(H)$
.
The following result parametrizes congruence classes of finite sets in
![]() $\mathbb {CH}^{n}$
as well as rescaling equivalence classes of
$\mathbb {CH}^{n}$
as well as rescaling equivalence classes of
![]() $\mathcal {RK}$
with the CPP.
$\mathcal {RK}$
with the CPP.
Theorem 5.1
-
(1) Given
 $X=\left \{ x_{i}\right \} _{i=1}^{n+1}\subset \mathbb {CH}^{n}$
, each entry of
$X=\left \{ x_{i}\right \} _{i=1}^{n+1}\subset \mathbb {CH}^{n}$
, each entry of
 $\rho (X)$
is between
$\rho (X)$
is between
 $0$
and 1, and
$0$
and 1, and
 $\mathcal {M}(X)$
is a positive-semidefinite matrix with
$\mathcal {M}(X)$
is a positive-semidefinite matrix with
 $1$
’s on the diagonal.
$1$
’s on the diagonal. -
(2) Conversely, given such a
 $\rho $
and
$\rho $
and
 $\mathcal {M}$
, there is an X so that
$\mathcal {M}$
, there is an X so that
 $\rho =\rho (X)$
and
$\rho =\rho (X)$
and
 $\mathcal {M}=\mathcal {M}(X).$
$\mathcal {M}=\mathcal {M}(X).$
-
(3) Given
 $Y\subset \mathbb {CH}^{n}$
,
$Y\subset \mathbb {CH}^{n}$
,
 $X\sim Y$
if and only if
$X\sim Y$
if and only if
 $\rho (X)=\rho (Y)$
and the matrices
$\rho (X)=\rho (Y)$
and the matrices
 $\mathcal {M}(X)$
and
$\mathcal {M}(X)$
and
 $\mathcal {M}(Y)$
are unitarily equivalent.
$\mathcal {M}(Y)$
are unitarily equivalent. -
(4) If
 $H\in \mathcal {RK}$
, then H has the CPP if and only if
$H\in \mathcal {RK}$
, then H has the CPP if and only if
 $\rho (H)$
and
$\rho (H)$
and
 $\mathcal {M}(H)$
satisfy the conditions in (1). If that happens, then
$\mathcal {M}(H)$
satisfy the conditions in (1). If that happens, then
 $H\sim DA(X)$
with X given by condition (2).
$H\sim DA(X)$
with X given by condition (2).
Proof In (1), the claim for
![]() $\rho (X)$
is clear. The matrix
$\rho (X)$
is clear. The matrix
![]() $\mathcal {M}(X)$
is invariant under automorphisms of
$\mathcal {M}(X)$
is invariant under automorphisms of
![]() $\mathbb {CH}^{n}$
, and hence we can suppose
$\mathbb {CH}^{n}$
, and hence we can suppose
![]() $x_{1}$
is at the origin. Let
$x_{1}$
is at the origin. Let
![]() $\widehat {X}$
be set of radial projections of the remaining points onto the unit sphere,
$\widehat {X}$
be set of radial projections of the remaining points onto the unit sphere,
![]() $\widehat {X}=\{\widehat {x_{2} },...,\widehat {x_{n+1}}\}\subset \mathbb {\partial B}_{n}.$
We then see from (2.14) that
$\widehat {X}=\{\widehat {x_{2} },...,\widehat {x_{n+1}}\}\subset \mathbb {\partial B}_{n}.$
We then see from (2.14) that
![]() $K_{ij}=\left \langle \left \langle \widehat {x_{i} },\widehat {x_{j}}\right \rangle \right \rangle $
for
$K_{ij}=\left \langle \left \langle \widehat {x_{i} },\widehat {x_{j}}\right \rangle \right \rangle $
for
![]() $2\leq i,j\leq n+1.$
Thus,
$2\leq i,j\leq n+1.$
Thus,
![]() $\mathcal {M}(X)$
is the Gram matrix of the set of vectors
$\mathcal {M}(X)$
is the Gram matrix of the set of vectors
![]() $\widehat {X}$
and hence is positive semidefinite. For (2), a matrix with the properties of
$\widehat {X}$
and hence is positive semidefinite. For (2), a matrix with the properties of
![]() $\mathcal {M}$
must be the Gram matrix of a set
$\mathcal {M}$
must be the Gram matrix of a set
![]() $W=\left \{ w_{i}\right \} _{i=2}^{n+1}\subset \mathbb {C}^{n}$
, unique up to unitary equivalence. The
$W=\left \{ w_{i}\right \} _{i=2}^{n+1}\subset \mathbb {C}^{n}$
, unique up to unitary equivalence. The
![]() $1$
’s on the diagonal of
$1$
’s on the diagonal of
![]() $\mathcal {M}$
insure that
$\mathcal {M}$
insure that
![]() $W\subset \partial \mathbb {B}_{n}.$
We now form X by designating the origin as
$W\subset \partial \mathbb {B}_{n}.$
We now form X by designating the origin as
![]() $x_{1}$
and for
$x_{1}$
and for
![]() $2\leq i\leq n+1$
picking
$2\leq i\leq n+1$
picking
![]() $x_{i}$
on the line segment
$x_{i}$
on the line segment
![]() $\left [ 0,w_{i}\right ] $
with
$\left [ 0,w_{i}\right ] $
with
![]() $\left \vert x_{i}\right \vert =\delta (x_{1}.x_{i}).$
It is straightforward that X has the required properties.
$\left \vert x_{i}\right \vert =\delta (x_{1}.x_{i}).$
It is straightforward that X has the required properties.
For (3), first suppose Y is congruent to
![]() $X;$
that is, Y is the image of X under an automorphism of the ball. The entries of
$X;$
that is, Y is the image of X under an automorphism of the ball. The entries of
![]() $\rho $
and
$\rho $
and
![]() $\mathcal {M}$
are automorphism invariants, and this gives the desired equalities. In the other direction, suppose the data associated with X equal the data associated with
$\mathcal {M}$
are automorphism invariants, and this gives the desired equalities. In the other direction, suppose the data associated with X equal the data associated with
![]() $Y.$
Without loss of generality, we can suppose
$Y.$
Without loss of generality, we can suppose
![]() $x_{1}$
is at the origin in which case
$x_{1}$
is at the origin in which case
![]() $\mathcal {M}(X)$
is the Gram matrix of the set
$\mathcal {M}(X)$
is the Gram matrix of the set
![]() $\widehat {X}\subset \partial \mathbb {B}_{n}$
. Similarly for Y and
$\widehat {X}\subset \partial \mathbb {B}_{n}$
. Similarly for Y and
![]() $\widehat {Y}.$
Thus,
$\widehat {Y}.$
Thus,
![]() $\widehat {X}$
and
$\widehat {X}$
and
![]() $\widehat {Y}$
have the same Gram matrix, and hence there is a unitary map
$\widehat {Y}$
have the same Gram matrix, and hence there is a unitary map
![]() $\mathbb {C}^{n}$
which takes
$\mathbb {C}^{n}$
which takes
![]() $\widehat {X}$
to
$\widehat {X}$
to
![]() $\widehat {Y}.$
That unitary is also an automorphism
$\widehat {Y}.$
That unitary is also an automorphism
![]() $\mathbb {CH}^{n}$
and so takes each segment connecting the origin to a point of
$\mathbb {CH}^{n}$
and so takes each segment connecting the origin to a point of
![]() $\widehat {X}$
to a segment connecting the origin to a point of
$\widehat {X}$
to a segment connecting the origin to a point of
![]() $\widehat {Y}.$
Given the further assumption that
$\widehat {Y}.$
Given the further assumption that
![]() $\rho (X)=\rho (Y)$
, it must take X to
$\rho (X)=\rho (Y)$
, it must take X to
![]() $Y,$
as required.
$Y,$
as required.
The final statement follows from the first three together with the fact that
![]() $\rho (H)$
and
$\rho (H)$
and
![]() $\mathcal {M}(H)$
determine H up to rescaling.
$\mathcal {M}(H)$
determine H up to rescaling.
Thus the congruence class of a set X of k (
![]() $=n+1)$
points in
$=n+1)$
points in
![]() $\mathbb {CH}^{m}$
,
$\mathbb {CH}^{m}$
,
![]() $m\geq k-1,$
is determined by the
$m\geq k-1,$
is determined by the
![]() $k-1$
real numbers in
$k-1$
real numbers in
![]() $\rho (X)$
together with the
$\rho (X)$
together with the
![]() $(k-1)(k-2)/2$
complex numbers which specify,
$(k-1)(k-2)/2$
complex numbers which specify,
![]() $\mathcal {M}(X)$
a positive semidefinite matrix with ones on the diagonal. Together these give
$\mathcal {M}(X)$
a positive semidefinite matrix with ones on the diagonal. Together these give
![]() $(k-1)^{2}$
real parameters, as expected. We should emphasize that
$(k-1)^{2}$
real parameters, as expected. We should emphasize that
![]() $\rho (X)$
and
$\rho (X)$
and
![]() $\mathcal {M}(X)$
only depend on the congruence class of ordered set X. The choice of which element is placed at the origin by an automorphism substantially affects all the values in
$\mathcal {M}(X)$
only depend on the congruence class of ordered set X. The choice of which element is placed at the origin by an automorphism substantially affects all the values in
![]() $\rho (X)$
and
$\rho (X)$
and
![]() $\mathcal {M}(X)$
. Once that point is specified, the remaining ordering only affects the ordering of the entries in
$\mathcal {M}(X)$
. Once that point is specified, the remaining ordering only affects the ordering of the entries in
![]() $\rho (X)$
and
$\rho (X)$
and
![]() $\mathcal {M}(X).$
$\mathcal {M}(X).$
Details of
![]() $\mathcal {M}(X)$
contain information about the geometry of
$\mathcal {M}(X)$
contain information about the geometry of
![]() $X.$
From the previous theorem and proof, we have the following corollary.
$X.$
From the previous theorem and proof, we have the following corollary.
Corollary 5.2 If the rank of
![]() $\mathcal {M}(X)$
is m, then X is congruent to a set in
$\mathcal {M}(X)$
is m, then X is congruent to a set in
![]() $\mathbb {CH}^{m}$
but is not congruent to a set in
$\mathbb {CH}^{m}$
but is not congruent to a set in
![]() $\mathbb {CH}^{j}$
for any
$\mathbb {CH}^{j}$
for any
![]() $j<m.$
In particular, if the rank is
$j<m.$
In particular, if the rank is
![]() $1$
, then X is contained in a complex geodesic.
$1$
, then X is contained in a complex geodesic.
Here are the details of
![]() $\rho (X)$
and
$\rho (X)$
and
![]() $\mathcal {M}(X)$
in some simple cases. Suppose
$\mathcal {M}(X)$
in some simple cases. Suppose
![]() $n+1=3$
. From Theorem 3.1, we know that the congruence class of the triangle
$n+1=3$
. From Theorem 3.1, we know that the congruence class of the triangle
![]() $X=\{x_{1},x_{2},x_{3}\}$
is described by the set
$X=\{x_{1},x_{2},x_{3}\}$
is described by the set
![]() $S^{\prime \prime }=(\delta _{12},\delta _{13},\operatorname *{kos}_{1}(2,3)).$
In the notation of the previous theorem,
$S^{\prime \prime }=(\delta _{12},\delta _{13},\operatorname *{kos}_{1}(2,3)).$
In the notation of the previous theorem,
 $$\begin{align*}\rho(X)=\left( \delta_{12},\delta_{13}\right) ,\text{ }\mathcal{M}(X)= \begin{pmatrix} 1 & \operatorname*{kos}_{1}(2,3)\\ \operatorname*{kos}_{1}(3,2) & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\rho(X)=\left( \delta_{12},\delta_{13}\right) ,\text{ }\mathcal{M}(X)= \begin{pmatrix} 1 & \operatorname*{kos}_{1}(2,3)\\ \operatorname*{kos}_{1}(3,2) & 1 \end{pmatrix}. \end{align*}$$
In this case, the condition
![]() $\mathcal {M}(X)\succcurlyeq 0$
is equivalent to
$\mathcal {M}(X)\succcurlyeq 0$
is equivalent to
![]() $\left \vert \operatorname *{kos}_{1}(2,3)\right \vert \leq 1$
, which is the condition (3.5) in Theorem 3.1.
$\left \vert \operatorname *{kos}_{1}(2,3)\right \vert \leq 1$
, which is the condition (3.5) in Theorem 3.1.
The case of
![]() $n+1=4$
points is discussed in Section 6.
$n+1=4$
points is discussed in Section 6.
For
![]() $X\subset \mathbb {CH}^{1}$
, we use the complex coordinate of
$X\subset \mathbb {CH}^{1}$
, we use the complex coordinate of
![]() $\mathbb {C} ^{1}$
and write
$\mathbb {C} ^{1}$
and write
![]() $X=\left \{ r_{s}e^{i\theta _{s}}\right \} _{s=1}^{n+1}$
with
$X=\left \{ r_{s}e^{i\theta _{s}}\right \} _{s=1}^{n+1}$
with
![]() $r_{1}=0.$
Using the computations in Section 4.1, we see that
$r_{1}=0.$
Using the computations in Section 4.1, we see that
The automorphisms of
![]() $\mathbb {CH}^{1}$
which fix the base point are rotations. They do not change the entries in
$\mathbb {CH}^{1}$
which fix the base point are rotations. They do not change the entries in
![]() $\mathcal {M}(X)$
or the congruence class of
$\mathcal {M}(X)$
or the congruence class of
![]() $X.$
On the other hand, complex conjugation, which is not in
$X.$
On the other hand, complex conjugation, which is not in
![]() $\operatorname *{Aut}\mathbb {B}_{1},$
can change the matrix entries and the congruence class.
$\operatorname *{Aut}\mathbb {B}_{1},$
can change the matrix entries and the congruence class.
For
![]() $Y \ \subset RB_{2},$
the Beltrami–Klein model of
$Y \ \subset RB_{2},$
the Beltrami–Klein model of
![]() $\mathbb {RH}^{2},$
we use the polar coordinates of the containing
$\mathbb {RH}^{2},$
we use the polar coordinates of the containing
![]() $\mathbb {R}^{2}.$
We have
$\mathbb {R}^{2}.$
We have
![]() $Y=\left \{ \left ( r_{s},\theta _{s}\right ) \right \} _{s=1}^{n+1}$
with
$Y=\left \{ \left ( r_{s},\theta _{s}\right ) \right \} _{s=1}^{n+1}$
with
![]() $r_{1}=0.$
Now, using Section 4.1 gives
$r_{1}=0.$
Now, using Section 4.1 gives
In this case, the map
![]() $(r,\theta )\rightarrow (r,-\theta ),$
which looks like complex conjugation, is the restriction of an element of
$(r,\theta )\rightarrow (r,-\theta ),$
which looks like complex conjugation, is the restriction of an element of
![]() $\operatorname *{Aut} \mathbb {B}_{2}$
to
$\operatorname *{Aut} \mathbb {B}_{2}$
to
![]() $RB_{2},$
namely, the map
$RB_{2},$
namely, the map
![]() $\left ( z,w\right ) \rightarrow (z,-w).$
That map changes the sign of the
$\left ( z,w\right ) \rightarrow (z,-w).$
That map changes the sign of the
![]() $\theta ^{\prime }s$
, but that does not change
$\theta ^{\prime }s$
, but that does not change
![]() $\mathcal {M}(Y)$
or the congruence class of
$\mathcal {M}(Y)$
or the congruence class of
![]() $Y.$
$Y.$
The previous theorem also gives the extension to n-valent vertices of the results in Section 4.3 for bivalent and trivalent vertices. Suppose
![]() $\mathbf {V}$
is an n-valent vertex in
$\mathbf {V}$
is an n-valent vertex in
![]() $\mathbb {CH}^{n}$
with vertex point
$\mathbb {CH}^{n}$
with vertex point
![]() $x_{1}$
and rays
$x_{1}$
and rays
![]() $\left \{ \gamma _{1i}\right \} _{i=2}^{n+1}.$
We are only interested in congruence classes, and hence we suppose
$\left \{ \gamma _{1i}\right \} _{i=2}^{n+1}.$
We are only interested in congruence classes, and hence we suppose
![]() $x_{1}$
is at the origin. For
$x_{1}$
is at the origin. For
![]() $i=2,...,n+1$
, select a point
$i=2,...,n+1$
, select a point
![]() $x_{i}$
on
$x_{i}$
on
![]() $\gamma _{1i}$
and set
$\gamma _{1i}$
and set
![]() $X=\left \{ x_{i}\right \} _{i=1}^{n+1}.$
From the previous theorem, we know the congruence class of X is determined by
$X=\left \{ x_{i}\right \} _{i=1}^{n+1}.$
From the previous theorem, we know the congruence class of X is determined by
![]() $\mathcal {M}(X)$
and
$\mathcal {M}(X)$
and
![]() $\rho (X).$
Looking at that proof, we see that knowing
$\rho (X).$
Looking at that proof, we see that knowing
![]() $\mathcal {M}(X)$
is equivalent to knowing the congruence class of the projected set
$\mathcal {M}(X)$
is equivalent to knowing the congruence class of the projected set
![]() $\widehat {X}.$
From the definitions, we see that knowing
$\widehat {X}.$
From the definitions, we see that knowing
![]() $\widehat {X}$
is equivalent to knowing
$\widehat {X}$
is equivalent to knowing
![]() $\mathbf {V.}$
Hence, defining
$\mathbf {V.}$
Hence, defining
![]() $\mathcal {M}(\mathbf {V})$
to be
$\mathcal {M}(\mathbf {V})$
to be
![]() $\mathcal {M}(X)$
, we have the following corollary of the previous theorem.
$\mathcal {M}(X)$
, we have the following corollary of the previous theorem.
Corollary 5.3
-
(1) Given an n-valent vertex
 $\mathbf {V}$
in
$\mathbf {V}$
in
 $\mathbb {CH} ^{n}$
,
$\mathbb {CH} ^{n}$
,
 $\mathcal {M}(\mathbf {V})$
has
$\mathcal {M}(\mathbf {V})$
has
 $1$
’s on the diagonal and
$1$
’s on the diagonal and
 $\mathcal {M} (\mathbf {V})\succcurlyeq 0.$
$\mathcal {M} (\mathbf {V})\succcurlyeq 0.$
-
(2) Given
 $\mathcal {N} \ which$
satisfies those conditions, there is a
$\mathcal {N} \ which$
satisfies those conditions, there is a
 $\mathbf {V}$
in
$\mathbf {V}$
in
 $\mathbb {CH}^{n}$
with
$\mathbb {CH}^{n}$
with
 $\mathcal {M}(\mathbf {V})$
$\mathcal {M}(\mathbf {V})$
 $=\mathcal {N}$
.
$=\mathcal {N}$
. -
(3) Two such vertices are congruent if and only if they give the same matrix
 $\mathcal {M}.$
$\mathcal {M}.$
-
(4) Given
 $\left \{ z_{i}\right \} _{i=2}^{n+1}\subset \partial \mathbb {B} _{n}$
there is a
$\left \{ z_{i}\right \} _{i=2}^{n+1}\subset \partial \mathbb {B} _{n}$
there is a
 $\mathbf {V}$
in
$\mathbf {V}$
in
 $\mathbb {CH}^{n}$
with
$\mathbb {CH}^{n}$
with
 $\mathcal {M} (\mathbf {V})$
equal to the Gram matrix of
$\mathcal {M} (\mathbf {V})$
equal to the Gram matrix of
 $\left \{ z_{i}\right \} .$
$\left \{ z_{i}\right \} .$
5.2 Comparison with the McCullough–Quiggin theorem
Theorem 5.1 has some similarity to the McCullough–Quiggin theorem. Here is brief informal discussion of that relation; more details are in Chapters 7 and 8 of [Reference Agler and PickAM] and the Historical Notes to those chapters.
Recall that we are only considering finite-dimensional spaces.
The first observation is that our “definition of convenience,” that H has the CPP if and only if it is a rescaling of a space
![]() $DA(X),$
is actually inconvenient in this context. We need to distinguish between that definition and the actual complete Pick property (ACPP) defined in terms of extension properties of certain matrix multipliers on
$DA(X),$
is actually inconvenient in this context. We need to distinguish between that definition and the actual complete Pick property (ACPP) defined in terms of extension properties of certain matrix multipliers on
![]() $H.$
That property is defined and discussed in Chapter 5 of [Reference Agler and PickAM].
$H.$
That property is defined and discussed in Chapter 5 of [Reference Agler and PickAM].
Given H and
![]() $1\leq s\leq \dim H$
, we can form the matrices
$1\leq s\leq \dim H$
, we can form the matrices
![]() $\operatorname *{KOS}(H,s)$
as described in (2.15).
$\operatorname *{KOS}(H,s)$
as described in (2.15).
Consider now the following four conditions:
-
(1) H has the ACPP.
-
(2) H has the CPP.
-
(3) For each s,
 $1\leq s\leq \dim H$
,
$1\leq s\leq \dim H$
,
 $\operatorname *{KOS}(H,s)\succcurlyeq 0.$
$\operatorname *{KOS}(H,s)\succcurlyeq 0.$
-
(4) For some s,
 $1\leq s\leq \dim H$
,
$1\leq s\leq \dim H$
,
 $\operatorname *{KOS}(H,s)\succcurlyeq 0.$
$\operatorname *{KOS}(H,s)\succcurlyeq 0.$
We saw that if
![]() $H=DA(X)$
, then
$H=DA(X)$
, then
![]() $\operatorname *{KOS}(H,s)$
is a Gram matrix; hence, statement 2 implies statements 3 and 4.
$\operatorname *{KOS}(H,s)$
is a Gram matrix; hence, statement 2 implies statements 3 and 4.
The result of McCullough and Quiggin, Theorem 7.6 in [Reference Agler and PickAM], is that statements 1 and 3 are equivalent. (Their result actually uses an equivalent formulation based on matrices
![]() $\operatorname *{MQ}(H,s)$
defined at (2.16). Their result also involves matrices of all sizes, but in this finite-dimensional case, it suffices to only consider the matrices of maximum size.) It is a result of Agler and McCarthy, Theorem 8.2 in [Reference Agler and PickAM], that conditions 1 and 2 are equivalent. Combining these two results, we see that 3 implies 2.
$\operatorname *{MQ}(H,s)$
defined at (2.16). Their result also involves matrices of all sizes, but in this finite-dimensional case, it suffices to only consider the matrices of maximum size.) It is a result of Agler and McCarthy, Theorem 8.2 in [Reference Agler and PickAM], that conditions 1 and 2 are equivalent. Combining these two results, we see that 3 implies 2.
On the other hand, by Theorem 5.1, if condition 4 holds, then 2 holds; H is a rescaling of some
![]() $DA(X).$
Considering the details of the proof of Theorem 5.1, this is a simpler path to that conclusion than the path through condition 1. Also, it only requires information about a single matrix, condition 4 rather than 3. However, this path says nothing about the relationship between conditions 1 and 2, which is one of the centerpieces of the theory of spaces with the ACPP.
$DA(X).$
Considering the details of the proof of Theorem 5.1, this is a simpler path to that conclusion than the path through condition 1. Also, it only requires information about a single matrix, condition 4 rather than 3. However, this path says nothing about the relationship between conditions 1 and 2, which is one of the centerpieces of the theory of spaces with the ACPP.
5.3 Assembly questions
We now return to the assembly and coherence question we discussed in Section 3.1. We will consider questions of congruence involving subsets of sets in
![]() $\mathbb {CH}^{n};$
however, recall, as we commented earlier, that these are equivalent to questions about rescaling of regular subspaces of spaces in
$\mathbb {CH}^{n};$
however, recall, as we commented earlier, that these are equivalent to questions about rescaling of regular subspaces of spaces in
![]() $\mathcal {CPP}$
.
$\mathcal {CPP}$
.
The generalized version of Question 1 from the Introduction is: given a finite collection of finite sets
![]() $\left \{ Y_{i}\right \} $
in some
$\left \{ Y_{i}\right \} $
in some
![]() $\mathbb {CH}^{n}$
, is there an X in some
$\mathbb {CH}^{n}$
, is there an X in some
![]() $\mathbb {CH}^{m}$
which contains congruent copies of the various
$\mathbb {CH}^{m}$
which contains congruent copies of the various
![]() $Y_{i}?$
We may also impose requirements on the overlap of the copies of the
$Y_{i}?$
We may also impose requirements on the overlap of the copies of the
![]() $\left \{ Y_{i}\right \} $
inside of
$\left \{ Y_{i}\right \} $
inside of
![]() $X.$
In Section 3.1, we saw that meeting such overlap conditions may require congruence of certain subsets of the various
$X.$
In Section 3.1, we saw that meeting such overlap conditions may require congruence of certain subsets of the various
![]() $Y_{i}.$
If all those congruence constraints are satisfied, we write
$Y_{i}.$
If all those congruence constraints are satisfied, we write
![]() $\left \{ Y_{i}\right \} \rightrightarrows ??$
and if there is such an X, we write
$\left \{ Y_{i}\right \} \rightrightarrows ??$
and if there is such an X, we write
![]() $\left \{ Y_{i}\right \} \rightrightarrows \ X.$
$\left \{ Y_{i}\right \} \rightrightarrows \ X.$
For
![]() $X\subset \mathbb {CH}^{n}$
with distinguished base point
$X\subset \mathbb {CH}^{n}$
with distinguished base point
![]() $x_{1}$
, recall that we write
$x_{1}$
, recall that we write
![]() $\operatorname *{KOS}(X,1)$
as a shorthand for
$\operatorname *{KOS}(X,1)$
as a shorthand for
![]() $\operatorname *{KOS}(DA(X),1)$
. For each i, let
$\operatorname *{KOS}(DA(X),1)$
. For each i, let
![]() $1_{i}$
be that point in
$1_{i}$
be that point in
![]() $Y_{i}$
which is mapped to the base point
$Y_{i}$
which is mapped to the base point
![]() $x_{1}$
of X under the assumed congruences, with
$x_{1}$
of X under the assumed congruences, with
![]() $1_{i}$
an arbitrary point of Y
$1_{i}$
an arbitrary point of Y
![]() $_{1}$
if that definition is unfilled.
$_{1}$
if that definition is unfilled.
If
![]() $\left \{ Y_{i}\right \} \rightrightarrows \ X$
, then, as we noted in Section 3.1, we can use data from the matrices
$\left \{ Y_{i}\right \} \rightrightarrows \ X$
, then, as we noted in Section 3.1, we can use data from the matrices
![]() $\operatorname *{KOS} (Y_{i},1_{i})$
to compute some of the entries
$\operatorname *{KOS} (Y_{i},1_{i})$
to compute some of the entries
![]() $\operatorname *{KOS}(X,1)$
and those computations can be done even without knowing if there is an
$\operatorname *{KOS}(X,1)$
and those computations can be done even without knowing if there is an
![]() $X.$
The computations produce a (possibly only partially filled) matrix, which we denote
$X.$
The computations produce a (possibly only partially filled) matrix, which we denote
![]() $\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1),$
$\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1),$
We now study the possibility that there is an X by comparing
![]() $\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
with the properties which we know from Theorem 5.1 that
$\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
with the properties which we know from Theorem 5.1 that
![]() $\operatorname *{KOS}(X,1)$
must have. More specifically, from our previous analysis culminating in Theorem 5.1, we know that the congruence class of X is described by a vector of side lengths,
$\operatorname *{KOS}(X,1)$
must have. More specifically, from our previous analysis culminating in Theorem 5.1, we know that the congruence class of X is described by a vector of side lengths,
![]() $\rho (X),$
and the matrix
$\rho (X),$
and the matrix
![]() $\mathcal {M(}X)=\operatorname *{KOS}(X,1).$
We extract information from
$\mathcal {M(}X)=\operatorname *{KOS}(X,1).$
We extract information from
![]() $\operatorname *{KOS}(X,1)$
by working with the principal submatrices. From the definitions, we have the following lemma.
$\operatorname *{KOS}(X,1)$
by working with the principal submatrices. From the definitions, we have the following lemma.
Lemma 5.4 If
![]() $H\in \mathcal {RK}$
, then the principal submatrices,
$H\in \mathcal {RK}$
, then the principal submatrices,
![]() $\mathcal {PS}(\operatorname *{KOS}(H,1)),$
are the matrices
$\mathcal {PS}(\operatorname *{KOS}(H,1)),$
are the matrices
![]() $\operatorname *{KOS}(J,1)$
for J which are regular subspaces of H which contain the kernel function
$\operatorname *{KOS}(J,1)$
for J which are regular subspaces of H which contain the kernel function
![]() $k_{1}.$
In particular, if
$k_{1}.$
In particular, if
![]() $H=DA(X)$
, then they are the matrices
$H=DA(X)$
, then they are the matrices
![]() $\operatorname *{KOS}(Y,1)$
for each Y which is a subset of X which contains the distinguished point.
$\operatorname *{KOS}(Y,1)$
for each Y which is a subset of X which contains the distinguished point.
The following classical result will let us relate the fact that
![]() $\mathcal {M(} X\mathcal {)}\succcurlyeq 0$
to properties of its principal submatrices
$\mathcal {M(} X\mathcal {)}\succcurlyeq 0$
to properties of its principal submatrices
![]() $\mathcal {PS}(\mathcal {M(}X\mathcal {))}$
.
$\mathcal {PS}(\mathcal {M(}X\mathcal {))}$
.
Lemma 5.5 (Sylvester’s criterion)
An
![]() $n\times n$
matrix A satisfies
$n\times n$
matrix A satisfies
![]() $A\succcurlyeq 0$
if and only if
$A\succcurlyeq 0$
if and only if
![]() $\det B\geq 0$
for all
$\det B\geq 0$
for all
![]() $B\in \mathcal {PS} {\large (A),}$
that is, if and only if the principal minors of A are nonnegative.
$B\in \mathcal {PS} {\large (A),}$
that is, if and only if the principal minors of A are nonnegative.
![]() $A\succ 0$
if and only if the leading principal minors are positive.
$A\succ 0$
if and only if the leading principal minors are positive.
Now, we look at three special cases, the case where the
![]() $\left \{ Y_{i}\right \} $
are three point sets whose congruent images fill an
$\left \{ Y_{i}\right \} $
are three point sets whose congruent images fill an
![]() $n+1$
point set, the question of specifying the geometry of the n point subsets of a set of
$n+1$
point set, the question of specifying the geometry of the n point subsets of a set of
![]() $n+1$
points, and after those general questions, we consider specific ad hoc variation chosen to show how these ideas work in a more complicated situation.
$n+1$
points, and after those general questions, we consider specific ad hoc variation chosen to show how these ideas work in a more complicated situation.
In the next section, we use these ideas for a systematic study of the question in the introduction of assembling four triangles into a tetrahedron.
5.3.1 Variation 1
We know from Theorem 3.2 that the congruence class of a set X is determined by the congruence classes of the triangles in X which contain a specified base point. We now ask if a given set of triangles can be congruent to those faces of some
![]() $X.$
We want to know if we can map triangles
$X.$
We want to know if we can map triangles
![]() $\left \{ Y_{i}\right \} _{i=1}^{n}$
in
$\left \{ Y_{i}\right \} _{i=1}^{n}$
in
![]() $\mathbb {CH}^{n},$
$\mathbb {CH}^{n},$
 $$\begin{align*} Y_{j} & =\left\{ y_{j1},y_{j,j+1},y_{j,j+2}\right\} ,\text{ } \ j<n,\\ Y_{n} & =\left\{ y_{n1},y_{n,n+1},y_{n2}\right\} , \end{align*}$$
$$\begin{align*} Y_{j} & =\left\{ y_{j1},y_{j,j+1},y_{j,j+2}\right\} ,\text{ } \ j<n,\\ Y_{n} & =\left\{ y_{n1},y_{n,n+1},y_{n2}\right\} , \end{align*}$$
into a set
![]() $X=\left \{ x_{1},...,x_{n+1}\right \} $
with each
$X=\left \{ x_{1},...,x_{n+1}\right \} $
with each
![]() $y_{jk}$
is mapped to
$y_{jk}$
is mapped to
![]() $x_{k}.$
That is, each image has its first vertex at
$x_{k}.$
That is, each image has its first vertex at
![]() $x_{1}$
and the images fill X with each segment
$x_{1}$
and the images fill X with each segment
![]() $x_{1}x_{t}$
in X covered twice. The coherence conditions are that two triangle sides that cover the same
$x_{1}x_{t}$
in X covered twice. The coherence conditions are that two triangle sides that cover the same
![]() $x_{1}x_{t}$
must be the same length.
$x_{1}x_{t}$
must be the same length.
Recall that the matrix
![]() $\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
is defined in (2.15).
$\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
is defined in (2.15).
Theorem 5.6 Given the coherence data
![]() $\left \{ Y_{i}\right \} \rightrightarrows \,??$
just described, the following are equivalent:
$\left \{ Y_{i}\right \} \rightrightarrows \,??$
just described, the following are equivalent:
-
(1)
 $\exists X$
,
$\exists X$
,
 $\left \{ Y_{i}\right \} \rightrightarrows X.$
$\left \{ Y_{i}\right \} \rightrightarrows X.$
-
(2)
 $\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)\succcurlyeq 0$
.
$\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)\succcurlyeq 0$
. -
(3)
 $\forall A\in \mathcal {PS(}\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))$
,
$\forall A\in \mathcal {PS(}\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))$
,
 $\det A\geq 0.$
$\det A\geq 0.$
-
(4)
 $\forall S\subset \left \{ 1,...,n\right \}$
,
$\forall S\subset \left \{ 1,...,n\right \}$
,
 $1\in S$
,
$1\in S$
,
 $\det \operatorname *{KOS}(\left \{ Y_{i}\right \} _{y\in S},1)\geq 0.$
$\det \operatorname *{KOS}(\left \{ Y_{i}\right \} _{y\in S},1)\geq 0.$
Taking note of Corollary 3.3, we also have the same result for spaces
![]() $J_{i}\in \mathcal {CPP}$
and the question of moving from
$J_{i}\in \mathcal {CPP}$
and the question of moving from
![]() $\left \{ J_{i}\right \} \rightrightarrows \,??$
to
$\left \{ J_{i}\right \} \rightrightarrows \,??$
to
![]() $\left \{ J_{i}\right \} \rightrightarrows H$
with
$\left \{ J_{i}\right \} \rightrightarrows H$
with
![]() $H\in \mathcal {CPP}$
.
$H\in \mathcal {CPP}$
.
For both
![]() $\left \{ Y_{i}\right \} $
and
$\left \{ Y_{i}\right \} $
and
![]() $\left \{ J_{i}\right \} $
, the condition
$\left \{ J_{i}\right \} $
, the condition
![]() $\det A\geq 0$
is automatic for the A that are
$\det A\geq 0$
is automatic for the A that are
![]() $1\times 1$
principal submatrices and the
$1\times 1$
principal submatrices and the
![]() $2\times 2$
case is insured by Theorem 3.1
$2\times 2$
case is insured by Theorem 3.1
![]() $.$
For A that are
$.$
For A that are
![]() $3\times 3$
, the situation is more complicated. For instance, if we suppose
$3\times 3$
, the situation is more complicated. For instance, if we suppose
![]() $\left \{ J_{i}\right \} \subset \mathcal {RK}$
but not necessarily in
$\left \{ J_{i}\right \} \subset \mathcal {RK}$
but not necessarily in
![]() $\mathcal {CPP}$
, then
$\mathcal {CPP}$
, then
![]() $\det A\geq 0$
is not automatic; see the comment after Theorem 6.4.
$\det A\geq 0$
is not automatic; see the comment after Theorem 6.4.
The case
![]() $n=3$
of this result is the tetrahedron assembly question of the introduction. We discuss it in more detail in the next section.
$n=3$
of this result is the tetrahedron assembly question of the introduction. We discuss it in more detail in the next section.
5.3.2 Variation 2
Suppose we are given
![]() $\left \{ Y_{i}\right \} _{i=1}^{n},$
sets of size n in
$\left \{ Y_{i}\right \} _{i=1}^{n},$
sets of size n in
![]() $\mathbb {CH}^{n}$
. Write
$\mathbb {CH}^{n}$
. Write
![]() $Y_{i}=\left \{ y_{ij}:1\leq j\leq n+1,\text { }j\neq i+1\right \} .$
We impose the coherence conditions
$Y_{i}=\left \{ y_{ij}:1\leq j\leq n+1,\text { }j\neq i+1\right \} .$
We impose the coherence conditions
![]() $\left \{ Y_{i}\right \} \rightrightarrows \,??$
that would hold if there were a set
$\left \{ Y_{i}\right \} \rightrightarrows \,??$
that would hold if there were a set
and congruences
![]() $Y_{i}\leadsto X$
which mapped the points
$Y_{i}\leadsto X$
which mapped the points
![]() $y_{is}$
to
$y_{is}$
to
![]() $x_{s},$
for all
$x_{s},$
for all
![]() $s\neq i.$
Informally, we are trying to specify the congruence type of all the subsets of size n inside a set of size
$s\neq i.$
Informally, we are trying to specify the congruence type of all the subsets of size n inside a set of size
![]() $n+1.$
This coherence condition
$n+1.$
This coherence condition
![]() $\left \{ Y_{i}\right \} \rightrightarrows \,??$
requires strong interrelations between the
$\left \{ Y_{i}\right \} \rightrightarrows \,??$
requires strong interrelations between the
![]() $Y_{i}$
. Given
$Y_{i}$
. Given
![]() $Y_{r}$
and
$Y_{r}$
and
![]() $Y_{s}$
, there are
$Y_{s}$
, there are
![]() $Y_{rs}\subset Y_{r}$
and
$Y_{rs}\subset Y_{r}$
and
![]() $Y_{sr}\subset Y_{s}$
both of size
$Y_{sr}\subset Y_{s}$
both of size
![]() $n-1$
with
$n-1$
with
![]() $Y_{rs}\sim Y_{sr}$
. Also, note that every
$Y_{rs}\sim Y_{sr}$
. Also, note that every
![]() $A\in \mathcal {PS(} \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))$
which is not maximal,
$A\in \mathcal {PS(} \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))$
which is not maximal,
![]() $A\neq \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1),$
satisfies
$A\neq \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1),$
satisfies
![]() $A\in \mathcal {PS(}\operatorname *{KOS}(Y_{r},1))$
for some individual
$A\in \mathcal {PS(}\operatorname *{KOS}(Y_{r},1))$
for some individual
![]() $Y_{r}.$
We know
$Y_{r}.$
We know
![]() $\operatorname *{KOS}(Y_{r},1)\succcurlyeq 0$
, and hence, by Sylvester’s criterion,
$\operatorname *{KOS}(Y_{r},1)\succcurlyeq 0$
, and hence, by Sylvester’s criterion,
![]() $\det A\geq 0.$
In sum, the only
$\det A\geq 0.$
In sum, the only
![]() ${A\in \mathcal {PS(} \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))}$
for which we do not know
${A\in \mathcal {PS(} \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1))}$
for which we do not know
![]() $\det A\geq 0$
is the matrix
$\det A\geq 0$
is the matrix
![]() $\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
itself. This discussion, together with Theorem 5.1, and the previous two lemmas, complete the proof of the following.
$\operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)$
itself. This discussion, together with Theorem 5.1, and the previous two lemmas, complete the proof of the following.
Theorem 5.7 Given
![]() $\left \{ Y_{i}\right \} \rightrightarrows \,??$
, there is an X so that
$\left \{ Y_{i}\right \} \rightrightarrows \,??$
, there is an X so that
![]() $\left \{ Y_{i}\right \} \rightrightarrows X$
if and only if
$\left \{ Y_{i}\right \} \rightrightarrows X$
if and only if
![]() $\det \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)\geq 0$
.
$\det \operatorname *{KOS}(\left \{ Y_{i}\right \} ,1)\geq 0$
.
5.3.3 Variation 3
We just looked at cases where the coherence requirements on the
![]() $\left \{ Y_{i}\right \} $
were minimal and maximal. We now look at an intermediate case which is rich enough to display some structure and simple enough for explicit computations.
$\left \{ Y_{i}\right \} $
were minimal and maximal. We now look at an intermediate case which is rich enough to display some structure and simple enough for explicit computations.
Suppose we are given two four-point sets in
![]() $\mathbb {CH}^{n}$
,
$\mathbb {CH}^{n}$
,
![]() $Y_{A}=\left \{ a_{1},a_{2},a_{3},a_{4}\right \} $
and
$Y_{A}=\left \{ a_{1},a_{2},a_{3},a_{4}\right \} $
and
![]() ${Y_{B}=\left \{ b_{1},b_{3},b_{4} ,b_{5}\right \}} $
. The coherence requirements,
${Y_{B}=\left \{ b_{1},b_{3},b_{4} ,b_{5}\right \}} $
. The coherence requirements,
![]() $\left \{ Y_{A},Y_{B}\right \} \rightrightarrows \,??,$
we impose are the congruences that would hold if we had maps
$\left \{ Y_{A},Y_{B}\right \} \rightrightarrows \,??,$
we impose are the congruences that would hold if we had maps
![]() $Y_{A},Y_{B}\leadsto X=\left \{ x_{1},...,x_{5}\right \} $
which respect the subscripts of the points. If that holds, then the triangles
$Y_{A},Y_{B}\leadsto X=\left \{ x_{1},...,x_{5}\right \} $
which respect the subscripts of the points. If that holds, then the triangles
![]() $A=\left \{ a_{1},a_{3},a_{4}\right \} $
and
$A=\left \{ a_{1},a_{3},a_{4}\right \} $
and
![]() $B=\left \{ b_{1},b_{3} ,b_{4}\right \} $
are congruent, and that congruence is the only coherence requirement.
$B=\left \{ b_{1},b_{3} ,b_{4}\right \} $
are congruent, and that congruence is the only coherence requirement.
We should not expect to fill the matrix
![]() $\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1).$
The set X has five points and so is determined by
$\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1).$
The set X has five points and so is determined by
![]() $\left ( 5-1\right ) ^{2}=16$
real parameters. On the other hand, each of Y’s provides nine parameters, but four of those are pinned by the fact that triangles A and B are congruent, leaving 14. This suggests that our description is two real or one complex parameter short of being able to fully describe
$\left ( 5-1\right ) ^{2}=16$
real parameters. On the other hand, each of Y’s provides nine parameters, but four of those are pinned by the fact that triangles A and B are congruent, leaving 14. This suggests that our description is two real or one complex parameter short of being able to fully describe
![]() $X.$
In fact, we cannot construct the entry
$X.$
In fact, we cannot construct the entry
![]() $\operatorname *{kos}_{1}(2,5)$
in the matrix
$\operatorname *{kos}_{1}(2,5)$
in the matrix
![]() $\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1)$
because neither the image of
$\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1)$
because neither the image of
![]() $Y_{A}$
nor of
$Y_{A}$
nor of
![]() $Y_{B}$
contain
$Y_{B}$
contain
![]() $\left \{ x_{1} ,x_{2},x_{5}\right \} .$
To move forward, we introduce a parameter z and fill the matrix
$\left \{ x_{1} ,x_{2},x_{5}\right \} .$
To move forward, we introduce a parameter z and fill the matrix
![]() $\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1)$
to a matrix
$\operatorname *{KOS}(\left \{ Y_{A},Y_{B}\right \} ,1)$
to a matrix
![]() $\mathcal {Y}= \ \operatorname *{KOS}(\left \{ Y_{A},Y_{B},z\right \} ,1)$
obtained from
$\mathcal {Y}= \ \operatorname *{KOS}(\left \{ Y_{A},Y_{B},z\right \} ,1)$
obtained from
![]() $\operatorname *{KOS}(\big \{ Y_{A},Y_{B}\big \} ,1)$
by putting z in the place where the
$\operatorname *{KOS}(\big \{ Y_{A},Y_{B}\big \} ,1)$
by putting z in the place where the
![]() $\operatorname *{kos}_{1}(2,5)$
entry would be, and
$\operatorname *{kos}_{1}(2,5)$
entry would be, and
![]() $\bar {z}$
where
$\bar {z}$
where
![]() $\operatorname *{kos}_{1}(5,2)$
would be. The values of z for which
$\operatorname *{kos}_{1}(5,2)$
would be. The values of z for which
![]() $\mathcal {Y} =\operatorname *{KOS}(\big \{ Y_{A} ,Y_{B},z\big \} ,1)\succcurlyeq 0$
, if any, will parameterize inequivalent possible constructions of the desired
$\mathcal {Y} =\operatorname *{KOS}(\big \{ Y_{A} ,Y_{B},z\big \} ,1)\succcurlyeq 0$
, if any, will parameterize inequivalent possible constructions of the desired
![]() $X.$
$X.$
We need to study the determinants of the matrices in
![]() $\mathcal {PS(Y}).$
$\mathcal {PS(Y}).$
![]() $\mathcal {Y}$
is a
$\mathcal {Y}$
is a
![]() $4\times 4$
matrix with rows and columns indexed by the set
$4\times 4$
matrix with rows and columns indexed by the set
![]() $\left \{ 2,3,4,5\right \} .$
The matrices in
$\left \{ 2,3,4,5\right \} .$
The matrices in
![]() $\mathcal {PS(Y})$
are determined by the 15 nonempty subsets of that index set. We denote those matrices by
$\mathcal {PS(Y})$
are determined by the 15 nonempty subsets of that index set. We denote those matrices by
![]() $\mathcal {Y}$
with subscripts denoting the rows, and hence also columns, of
$\mathcal {Y}$
with subscripts denoting the rows, and hence also columns, of
![]() $\mathcal {Y}$
that are retained. There are four single element subsets to consider, for each of them the resulting matrix has the single entry
$\mathcal {Y}$
that are retained. There are four single element subsets to consider, for each of them the resulting matrix has the single entry
![]() $1$
and hence a positive determinant. There are six possibilities with two subscripts. The matrix
$1$
and hence a positive determinant. There are six possibilities with two subscripts. The matrix
![]() $\mathcal {Y}_{34}$
will be a submatrix of both
$\mathcal {Y}_{34}$
will be a submatrix of both
![]() $\operatorname *{KOS} (Y_{A},1)$
and
$\operatorname *{KOS} (Y_{A},1)$
and
![]() $\operatorname *{KOS}(Y_{B},1)$
and hence, by Sylvester’s criterion, will have a positive determinant. The matrix
$\operatorname *{KOS}(Y_{B},1)$
and hence, by Sylvester’s criterion, will have a positive determinant. The matrix
![]() $\mathcal {Y}_{23}$
is not a submatrix of
$\mathcal {Y}_{23}$
is not a submatrix of
![]() $\operatorname *{KOS}(Y_{B},1),$
but it is a submatrix of
$\operatorname *{KOS}(Y_{B},1),$
but it is a submatrix of
![]() $\operatorname *{KOS}(Y_{A},1)$
and that is enough to insure it has a positive determinant. The same holds for
$\operatorname *{KOS}(Y_{A},1)$
and that is enough to insure it has a positive determinant. The same holds for
![]() $\mathcal {Y}_{24}$
, and a similar argument applies
$\mathcal {Y}_{24}$
, and a similar argument applies
![]() $\mathcal {Y}_{35}$
and
$\mathcal {Y}_{35}$
and
![]() $\mathcal {Y}_{45}$
but with the roles of A and B reversed. The remaining matrix of that size is
$\mathcal {Y}_{45}$
but with the roles of A and B reversed. The remaining matrix of that size is
![]() $\mathcal {Y}_{25};$
it cannot be studied using either
$\mathcal {Y}_{25};$
it cannot be studied using either
![]() $Y_{A}$
or
$Y_{A}$
or
![]() $Y_{B}.$
It is a
$Y_{B}.$
It is a
![]() $2\times 2$
matrix with 1’s on the diagonal and z and
$2\times 2$
matrix with 1’s on the diagonal and z and
![]() $\bar {z}$
as off diagonal elements, and it must be dealt with separately. If we do not know about
$\bar {z}$
as off diagonal elements, and it must be dealt with separately. If we do not know about
![]() $\det \mathcal {Y} _{25}$
, then we also cannot know the positive semidefinite nature of the matrices of which it as a submatrix, and hence those matrices must also be studied separately. They are
$\det \mathcal {Y} _{25}$
, then we also cannot know the positive semidefinite nature of the matrices of which it as a submatrix, and hence those matrices must also be studied separately. They are
![]() $\mathcal {Y}_{253}$
,
$\mathcal {Y}_{253}$
,
![]() $\mathcal {Y}_{254},$
and
$\mathcal {Y}_{254},$
and
![]() $\mathcal {Y}_{2534}=\mathcal {Y}.$
The two remaining submatrices are
$\mathcal {Y}_{2534}=\mathcal {Y}.$
The two remaining submatrices are
![]() $\mathcal {Y}_{234}=\operatorname *{KOS}(Y_{A},1)$
and
$\mathcal {Y}_{234}=\operatorname *{KOS}(Y_{A},1)$
and
![]() $\mathcal {Y} _{345}=\operatorname *{KOS}(Y_{B},1)$
, which we know are positive semidefinite.
$\mathcal {Y} _{345}=\operatorname *{KOS}(Y_{B},1)$
, which we know are positive semidefinite.
Theorem 5.8 There is an X so that
![]() $\left \{ Y_{A},Y_{B}\right \} \rightrightarrows X$
if and only if there is a z so that
$\left \{ Y_{A},Y_{B}\right \} \rightrightarrows X$
if and only if there is a z so that
![]() $\mathcal {Y=} \operatorname *{KOS}(\left \{ Y_{A},Y_{B},z\right \} ,1)\succcurlyeq 0,$
equivalently if and only if
$\mathcal {Y=} \operatorname *{KOS}(\left \{ Y_{A},Y_{B},z\right \} ,1)\succcurlyeq 0,$
equivalently if and only if
![]() $\mathcal {Y}$
and the submatrices
$\mathcal {Y}$
and the submatrices
![]() $\mathcal {Y} _{25}$
,
$\mathcal {Y} _{25}$
,
![]() $\mathcal {Y}_{253},$
and
$\mathcal {Y}_{253},$
and
![]() $\mathcal {Y}_{254}$
have positive determinants. The condition on
$\mathcal {Y}_{254}$
have positive determinants. The condition on
![]() $\mathcal {Y}_{25}$
holds exactly if
$\mathcal {Y}_{25}$
holds exactly if
![]() $\left \vert z\right \vert \leq 1$
; the other two determinants can be studied using (6.1).
$\left \vert z\right \vert \leq 1$
; the other two determinants can be studied using (6.1).
6 Tetrahedra
We now make the earlier conditions more explicit for four point sets and answer Questions 1 and 2 of the introduction. We also use the results to analyze a family of four-dimensional
![]() $\mathcal {RK}$
introduced by Quiggin.
$\mathcal {RK}$
introduced by Quiggin.
6.1 Question 1
We are given
![]() $\left \{ T_{i}\right \} _{1}^{4}$
a set of four triangles in
$\left \{ T_{i}\right \} _{1}^{4}$
a set of four triangles in
![]() $\mathbb {CH}^{n}$
which satisfy the coherence conditions for assembly into a tetrahedron,
$\mathbb {CH}^{n}$
which satisfy the coherence conditions for assembly into a tetrahedron,
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows ??,$
and we want to know if they can, in fact, be assembled into a tetrahedron
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows ??,$
and we want to know if they can, in fact, be assembled into a tetrahedron
![]() $X\subset \mathbb {CH}^{n}$
,
$X\subset \mathbb {CH}^{n}$
,
![]() $\left \{ T_{i}\right \} _{i=2}^{4} \rightrightarrows X.$
That can be done if and only if the parameter values imputed to X from the details of the
$\left \{ T_{i}\right \} _{i=2}^{4} \rightrightarrows X.$
That can be done if and only if the parameter values imputed to X from the details of the
![]() $\left \{ T_{i}\right \} $
and the coherence conditions describe a possible tetrahedron
$\left \{ T_{i}\right \} $
and the coherence conditions describe a possible tetrahedron
![]() $.$
We begin by reviewing those parameters.
$.$
We begin by reviewing those parameters.
Any tetrahedron in
![]() $\mathbb {CH}^{n}$
is congruent to one of the forms
$\mathbb {CH}^{n}$
is congruent to one of the forms
![]() $X=\left \{ 0,x_{2},x_{3},x_{4}\right \} \subset \mathbb {CH}^{2}.$
Here, we identify
$X=\left \{ 0,x_{2},x_{3},x_{4}\right \} \subset \mathbb {CH}^{2}.$
Here, we identify
![]() $\mathbb {CH}^{2}$
with the unit ball in
$\mathbb {CH}^{2}$
with the unit ball in
![]() $\mathbb {C}^{2}$
and also regard the
$\mathbb {C}^{2}$
and also regard the
![]() $\left \{ x_{i}\right \} $
as points in that space. Let
$\left \{ x_{i}\right \} $
as points in that space. Let
![]() $\mathbf {V}_{ij}$
be the bivalent vertex
$\mathbf {V}_{ij}$
be the bivalent vertex
![]() $x_{i}0x_{j}.$
From Theorem 5.1, we see that we must have each
$x_{i}0x_{j}.$
From Theorem 5.1, we see that we must have each
![]() $\left \vert x_{i}\right \vert <1$
and that the matrix
$\left \vert x_{i}\right \vert <1$
and that the matrix
must be positive semidefinite. We will make that last condition more explicit.
Lemma 6.1 Given
![]() $\left \{ a_{i}\right \} _{i=1}^{3} \subset \mathbb {C}$
with each
$\left \{ a_{i}\right \} _{i=1}^{3} \subset \mathbb {C}$
with each
![]() $\left \vert a_{i}\right \vert \leq 1,$
set
$\left \vert a_{i}\right \vert \leq 1,$
set
 $$\begin{align*}\mathcal{N}= \begin{pmatrix} 1 & a_{1} & a_{2}\\ \overline{a_{1}} & 1 & a_{3}\\ \overline{a_{2}} & \overline{a_{3}} & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{N}= \begin{pmatrix} 1 & a_{1} & a_{2}\\ \overline{a_{1}} & 1 & a_{3}\\ \overline{a_{2}} & \overline{a_{3}} & 1 \end{pmatrix}. \end{align*}$$
The following are equivalent:
-
(1)
 $0\preccurlyeq \mathcal {N}$
.
$0\preccurlyeq \mathcal {N}$
. -
(2)
 $0\leq \det \mathcal {N}.$
$0\leq \det \mathcal {N}.$
-
(3)
 $0\leq 1+2\operatorname {Re}a_{1}\overline {a_{2}}a_{3}-\left \vert a_{1}\right \vert ^{2}-\left \vert a_{2}\right \vert ^{2}-\left \vert a_{3}\right \vert ^{2}.$
$0\leq 1+2\operatorname {Re}a_{1}\overline {a_{2}}a_{3}-\left \vert a_{1}\right \vert ^{2}-\left \vert a_{2}\right \vert ^{2}-\left \vert a_{3}\right \vert ^{2}.$
-
(4)
 $\left \vert a_{1}\overline {a_{2}}-a_{3}\right \vert ^{2}\leq (1-\left \vert a_{1}\right \vert ^{2})(1-\left \vert a_{2}\right \vert ^{2}).$
$\left \vert a_{1}\overline {a_{2}}-a_{3}\right \vert ^{2}\leq (1-\left \vert a_{1}\right \vert ^{2})(1-\left \vert a_{2}\right \vert ^{2}).$
Proof By Sylvester’s criterion, the first condition implies the second. The second and third conditions are equivalent by definition. That the third and fourth are equivalent can be seen by expanding both sides of the fourth statement giving
Cancellation and rearrangement shows that is equivalent to the third statement.
To go in the other direction, we again use Sylvester’s criterion and show the second statement implies the first. That states that the first statement is a consequence of the nonnegativity of the seven principal minors. Three are the determinants of the
![]() ${1\times 1}$
matrices given by the diagonal entries and they are positive. The determinants of the three
${1\times 1}$
matrices given by the diagonal entries and they are positive. The determinants of the three
![]() $2\times 2$
submatrices are accounted for by the assumption on the size of the
$2\times 2$
submatrices are accounted for by the assumption on the size of the
![]() $a_{i}.$
Finally, the positivity of
$a_{i}.$
Finally, the positivity of
![]() $\det \mathcal {N}$
is the second statement.
$\det \mathcal {N}$
is the second statement.
We want to know if a set of four triangles in
![]() $\mathbb {CH}^{n}$
,
$\mathbb {CH}^{n}$
,
![]() $\left \{ T_{i}\right \} _{1}^{4}$
which satisfy
$\left \{ T_{i}\right \} _{1}^{4}$
which satisfy
![]() $\left \{ T_{i}\right \} _{i=1} ^{4}\rightrightarrows\ ??$
, might satisfy
$\left \{ T_{i}\right \} _{i=1} ^{4}\rightrightarrows\ ??$
, might satisfy
![]() $\left \{ T_{i}\right \} _{i=1} ^{4}\rightrightarrows X$
for some tetrahedron
$\left \{ T_{i}\right \} _{i=1} ^{4}\rightrightarrows X$
for some tetrahedron
![]() $X=\left \{ 0,x_{2},x_{3} ,x_{4}\right \} .$
By congruence invariance, we may suppose that for
$X=\left \{ 0,x_{2},x_{3} ,x_{4}\right \} .$
By congruence invariance, we may suppose that for
![]() $i=2,3,4$
, the triangle
$i=2,3,4$
, the triangle
![]() $T_{i}$
has vertices
$T_{i}$
has vertices
![]() $\left \{ 0,x_{i1},x_{i2}\right \} $
for various
$\left \{ 0,x_{i1},x_{i2}\right \} $
for various
![]() $x_{ij}$
of length at most one. The coherence requirements on the set of triangles insure that
$x_{ij}$
of length at most one. The coherence requirements on the set of triangles insure that
![]() $\left \vert x_{22}\right \vert =\left \vert x_{31}\right \vert $
,
$\left \vert x_{22}\right \vert =\left \vert x_{31}\right \vert $
,
![]() $\left \vert x_{32}\right \vert =\left \vert x_{41} \right \vert $
, and
$\left \vert x_{32}\right \vert =\left \vert x_{41} \right \vert $
, and
![]() $\left \vert x_{42}\right \vert =\left \vert x_{21}\right \vert .$
If the assembly of the triangles into an X is possible, these three quantities will be the side lengths
$\left \vert x_{42}\right \vert =\left \vert x_{21}\right \vert .$
If the assembly of the triangles into an X is possible, these three quantities will be the side lengths
![]() $\left \vert x_{2}\right \vert ,$
$\left \vert x_{2}\right \vert ,$
![]() $\left \vert x_{3}\right \vert ,$
and
$\left \vert x_{3}\right \vert ,$
and
![]() $\left \vert x_{4}\right \vert ,$
of X, and those lengths, the values of the
$\left \vert x_{4}\right \vert ,$
of X, and those lengths, the values of the
![]() $\rho $
of Theorem 5.1, can be any numbers between zero and one. Hence, it only remains to check if the values of
$\rho $
of Theorem 5.1, can be any numbers between zero and one. Hence, it only remains to check if the values of
![]() $\operatorname *{kos}\left ( \mathbf {V}_{ij}\right ) $
imputed from the triangles lead to a matrix
$\operatorname *{kos}\left ( \mathbf {V}_{ij}\right ) $
imputed from the triangles lead to a matrix
![]() $\mathcal {M}$
with the required properties. If assemble is possible, then the vertex
$\mathcal {M}$
with the required properties. If assemble is possible, then the vertex
![]() $\mathbf {V}_{23}$
of X will be (congruent to) the vertex of
$\mathbf {V}_{23}$
of X will be (congruent to) the vertex of
![]() $T_{2}$
at the origin, similarly for
$T_{2}$
at the origin, similarly for
![]() $\mathbf {V}_{34}$
and
$\mathbf {V}_{34}$
and
![]() $T_{3}$
,
$T_{3}$
,
![]() $\mathbf {V}_{42}$
and
$\mathbf {V}_{42}$
and
![]() $T_{4}.$
Thus,
$T_{4}.$
Thus,
![]() $\mathcal {M(}\left \{ T_{i}\right \} \mathcal {)}$
, the imputed value of
$\mathcal {M(}\left \{ T_{i}\right \} \mathcal {)}$
, the imputed value of
![]() $\mathcal {M(}X\mathcal {)}$
, is given by
$\mathcal {M(}X\mathcal {)}$
, is given by
 $$ \begin{align} \mathcal{M(}\left\{ T_{i}\right\} \mathcal{)}= \begin{pmatrix} 1 & \operatorname*{kos}(T_{2}) & \overline{\operatorname*{kos}(T_{4})}\\ \overline{\operatorname*{kos}(T_{2})} & 1 & \operatorname*{kos}(T_{3})\\ \operatorname*{kos}(T_{4}) & \overline{\operatorname*{kos}(T_{3})} & 1 \end{pmatrix} = \begin{pmatrix} 1 & K_{23} & K_{24}\\ K_{32} & 1 & K_{34}\\ K_{42} & K_{43} & 1 \end{pmatrix}, \end{align} $$
$$ \begin{align} \mathcal{M(}\left\{ T_{i}\right\} \mathcal{)}= \begin{pmatrix} 1 & \operatorname*{kos}(T_{2}) & \overline{\operatorname*{kos}(T_{4})}\\ \overline{\operatorname*{kos}(T_{2})} & 1 & \operatorname*{kos}(T_{3})\\ \operatorname*{kos}(T_{4}) & \overline{\operatorname*{kos}(T_{3})} & 1 \end{pmatrix} = \begin{pmatrix} 1 & K_{23} & K_{24}\\ K_{32} & 1 & K_{34}\\ K_{42} & K_{43} & 1 \end{pmatrix}, \end{align} $$
where the last equality defines the matrix
![]() $\left ( K_{ij}\right ) .$
$\left ( K_{ij}\right ) .$
We have collected all of the pieces to answer Question 1.
Theorem 6.2 With the numbering and naming scheme just described:
-
(1) There is an X such that
 $\left \{ T_{i}\right \} _{i=1}^{4} \rightrightarrows X$
if and only if there is an X such that
$\left \{ T_{i}\right \} _{i=1}^{4} \rightrightarrows X$
if and only if there is an X such that
 ${\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X}$
.
${\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X}$
. -
(2) If
 $\left \{ T_{i}\right \} \rightrightarrows X$
, then
$\left \{ T_{i}\right \} \rightrightarrows X$
, then
 $\mathcal {M} (\left \{ T_{i}\right \} )=\mathcal {M}(X)\succcurlyeq 0$
.
$\mathcal {M} (\left \{ T_{i}\right \} )=\mathcal {M}(X)\succcurlyeq 0$
. -
(3) If
 $\mathcal {M}(\left \{ T_{i}\right \} ) \ \succcurlyeq 0$
, then there is an X with
$\mathcal {M}(\left \{ T_{i}\right \} ) \ \succcurlyeq 0$
, then there is an X with
 $\left \{ T_{i}\right \} \rightrightarrows X.$
$\left \{ T_{i}\right \} \rightrightarrows X.$
-
(4)
 $\mathcal {M}(\left \{ T_{i}\right \} )\succcurlyeq 0$
if and only if
$\mathcal {M}(\left \{ T_{i}\right \} )\succcurlyeq 0$
if and only if
 $\det \mathcal {M}(X)\geq 0,$
equivalently if and only if (6.2)
$\det \mathcal {M}(X)\geq 0,$
equivalently if and only if (6.2) $$ \begin{align} \left\vert K_{34}-\overline{K_{23}}K_{24}\right\vert ^{2}\leq(1-\left\vert K_{23}\right\vert ^{2})(1-\left\vert K_{24}\right\vert ^{2}). \end{align} $$
$$ \begin{align} \left\vert K_{34}-\overline{K_{23}}K_{24}\right\vert ^{2}\leq(1-\left\vert K_{23}\right\vert ^{2})(1-\left\vert K_{24}\right\vert ^{2}). \end{align} $$
Proof The first statement is a consequence of the observation that our computation of the imputed values of
![]() $\rho (X)$
and
$\rho (X)$
and
![]() $\mathcal {M}(X)$
never used data from
$\mathcal {M}(X)$
never used data from
![]() $T_{1}.$
The next two statements follow from the discussion before the theorem together with Theorem 5.1. The final statement follows from the previous lemma together with statement (6) of Theorem 3.1, which insures that each
$T_{1}.$
The next two statements follow from the discussion before the theorem together with Theorem 5.1. The final statement follows from the previous lemma together with statement (6) of Theorem 3.1, which insures that each
![]() $\left \vert K_{ij}\right \vert \leq 1.$
$\left \vert K_{ij}\right \vert \leq 1.$
The condition (6.2) was obtained by specializing general results. However, in this low-dimensional case, we could have worked directly with the coordinates of
![]() $X=\Delta $
as described in (3.2). In that case, the
$X=\Delta $
as described in (3.2). In that case, the
![]() $K_{ij}$
can be computed using the points
$K_{ij}$
can be computed using the points
![]() $\{\widehat {x_{i}}\}_{i=2}^{4}$
on the unit sphere with coordinates
$\{\widehat {x_{i}}\}_{i=2}^{4}$
on the unit sphere with coordinates
 $$ \begin{align} & \widehat{x}_{2}=(1,0,0),\text{ }\widehat{x}_{3}=(\xi,\beta,0),\text{ }\widehat{x}_{4}=(\eta,\zeta,\gamma);\nonumber\\ & \beta,\gamma\geq0;\text{ }\xi,\eta,\zeta\in\mathbb{C}; \text{ }\nonumber\\ & \left\vert \xi\right\vert ^{2}+\beta^{2}=\left\vert \eta\right\vert ^{2}+\left\vert \zeta\right\vert ^{2}+\gamma^{2}=1. \end{align} $$
$$ \begin{align} & \widehat{x}_{2}=(1,0,0),\text{ }\widehat{x}_{3}=(\xi,\beta,0),\text{ }\widehat{x}_{4}=(\eta,\zeta,\gamma);\nonumber\\ & \beta,\gamma\geq0;\text{ }\xi,\eta,\zeta\in\mathbb{C}; \text{ }\nonumber\\ & \left\vert \xi\right\vert ^{2}+\beta^{2}=\left\vert \eta\right\vert ^{2}+\left\vert \zeta\right\vert ^{2}+\gamma^{2}=1. \end{align} $$
For
![]() $2\leq i,j\leq 4$
, we have
$2\leq i,j\leq 4$
, we have
![]() $K_{ii}=1$
,
$K_{ii}=1$
,
![]() $K_{ij}=\overline {K_{ji}}.$
The rest of the story is given by
$K_{ij}=\overline {K_{ji}}.$
The rest of the story is given by
We also have
Hence, noting that for all
![]() $i,j$
,
$i,j$
,
![]() $\left \vert K_{ij}\right \vert \leq 1,$
we must have
$\left \vert K_{ij}\right \vert \leq 1,$
we must have
which is (6.2). In the other direction, it is not hard to start from
![]() $\left \{ K_{ij}\right \} $
, which satisfy these conditions and find coordinates of points on the sphere which generate these data.
$\left \{ K_{ij}\right \} $
, which satisfy these conditions and find coordinates of points on the sphere which generate these data.
Our path to answering Question 1 had many digressions, and it is perhaps worthwhile to summarize the essential steps. First, if there is a tetrahedron, then the interpretation of
![]() $\operatorname *{kos}$
in (2.14) together with the definition
$\operatorname *{kos}$
in (2.14) together with the definition
![]() $\mathcal {M=M}(\left \{ T_{i}\right \} )$
insures that
$\mathcal {M=M}(\left \{ T_{i}\right \} )$
insures that
![]() $\mathcal {M}$
is a Gram matrix and hence is positive definite. In the other direction, given that
$\mathcal {M}$
is a Gram matrix and hence is positive definite. In the other direction, given that
![]() $\mathcal {M}$
is positive definite, it must be the Gram matrix of a three-point set on the sphere. Reversing the construction of that three-point set determines three points in the ball which, together with the origin, are the vertices of our candidate tetrahedron. To finish, we need to show that this candidate tetrahedron has faces in the correct congruence classes. For the faces that meet at the origin, this holds by the complex analog of the side-angle-side criterion for congruence of triangles, Remark 1. Proposition 4.6 then shows that that data determine the congruence class of the fourth face and the proof of that same proposition shows that that same congruence class is forced by the data of the first three triangles and the assumed coherence conditions.
$\mathcal {M}$
is positive definite, it must be the Gram matrix of a three-point set on the sphere. Reversing the construction of that three-point set determines three points in the ball which, together with the origin, are the vertices of our candidate tetrahedron. To finish, we need to show that this candidate tetrahedron has faces in the correct congruence classes. For the faces that meet at the origin, this holds by the complex analog of the side-angle-side criterion for congruence of triangles, Remark 1. Proposition 4.6 then shows that that data determine the congruence class of the fourth face and the proof of that same proposition shows that that same congruence class is forced by the data of the first three triangles and the assumed coherence conditions.
Here is a variation on these ideas. Given two triangles,
![]() $T_{2}$
and
$T_{2}$
and
![]() $T_{3},$
with one pair of matching side lengths, is it possible to find a third triangle
$T_{3},$
with one pair of matching side lengths, is it possible to find a third triangle
![]() $T_{4}$
so that
$T_{4}$
so that
![]() $\left \{ T_{i}\right \} _{2}^{4}\rightrightarrows X$
for some tetrahedron
$\left \{ T_{i}\right \} _{2}^{4}\rightrightarrows X$
for some tetrahedron
![]() $X?$
Again the question is whether the imputed parameters for X are an allowable set. If
$X?$
Again the question is whether the imputed parameters for X are an allowable set. If
![]() $T_{2}$
and
$T_{2}$
and
![]() $T_{3}$
are given and have a pair of matching side lengths, then all of the data for a putative
$T_{3}$
are given and have a pair of matching side lengths, then all of the data for a putative
![]() $\rho (X)$
are specified and, as required, each value is between zero and one. The value of
$\rho (X)$
are specified and, as required, each value is between zero and one. The value of
![]() $\operatorname *{kos}$
at the distinguished vertex of
$\operatorname *{kos}$
at the distinguished vertex of
![]() $T_{2}$
will give the value of
$T_{2}$
will give the value of
![]() $K_{23}$
for the potential matrix
$K_{23}$
for the potential matrix
![]() $\mathcal {M}$
, similarly for
$\mathcal {M}$
, similarly for
![]() $T_{3}$
and
$T_{3}$
and
![]() $K_{24}.$
However, the data from
$K_{24}.$
However, the data from
![]() $T_{2}$
and
$T_{2}$
and
![]() $T_{3}$
are not enough to compute
$T_{3}$
are not enough to compute
![]() $K_{42}$
, which would be the value of
$K_{42}$
, which would be the value of
![]() $\operatorname *{kos}$
at its distinguished vertex of
$\operatorname *{kos}$
at its distinguished vertex of
![]() $T_{4}$
. Hence, the congruence class of
$T_{4}$
. Hence, the congruence class of
![]() $T_{4}$
is indeterminate. To go forward, we set
$T_{4}$
is indeterminate. To go forward, we set
![]() $K_{42}=z$
, and using z, we complete the matrix
$K_{42}=z$
, and using z, we complete the matrix
![]() $\mathcal {M(}\left \{ T_{2},T_{3}\right \} )$
to a matrix
$\mathcal {M(}\left \{ T_{2},T_{3}\right \} )$
to a matrix
![]() $\mathcal {M}$
which has no missing values. We then apply the previous theorem to that matrix.
$\mathcal {M}$
which has no missing values. We then apply the previous theorem to that matrix.
Corollary 6.3 If
![]() $\left \{ T_{2},T_{3}\right \} \rightrightarrows \,??$
, then there are a third triangle
$\left \{ T_{2},T_{3}\right \} \rightrightarrows \,??$
, then there are a third triangle
![]() $T_{4}$
and a tetrahedron X with
$T_{4}$
and a tetrahedron X with
![]() $\left \{ T_{2} ,T_{3},T_{4}\right \} \rightrightarrows X$
if and only if the Euclidean ball in
$\left \{ T_{2} ,T_{3},T_{4}\right \} \rightrightarrows X$
if and only if the Euclidean ball in
![]() $\mathbb {C}^{1}$
$\mathbb {C}^{1}$
is nonempty. In that case, the pairing of z with the value
![]() $K_{34}$
establishes a one-to-one correspondence between
$K_{34}$
establishes a one-to-one correspondence between
![]() $z\in B$
and the congruence class of the possible third triangle
$z\in B$
and the congruence class of the possible third triangle
![]() $T_{4}.$
If B is empty, then there is no such
$T_{4}.$
If B is empty, then there is no such
![]() $T_{4}.$
$T_{4}.$
Proof Putting z into (6.2) gives
![]() $\left \vert z-\overline {K_{23}} K_{24}\right \vert ^{2}\leq (1-\left \vert K_{23}\right \vert ^{2})(1-\left \vert K_{24}\right \vert ^{2}).$
$\left \vert z-\overline {K_{23}} K_{24}\right \vert ^{2}\leq (1-\left \vert K_{23}\right \vert ^{2})(1-\left \vert K_{24}\right \vert ^{2}).$
6.2 Question 2
We saw in Section 3.2 that Question 2 is equivalent to Question 1. Having answered Question 1, we now reformulate that answer in the context of Question 2. We will be informal.
We start with four three-dimensional
![]() $\left \{ J_{i}\right \} _{i=1} ^{4}\subset \mathcal {CPP}$
and want to know if there is an
$\left \{ J_{i}\right \} _{i=1} ^{4}\subset \mathcal {CPP}$
and want to know if there is an
![]() $H\in \mathcal {CPP}$
whose four regular subspaces are rescalings of the
$H\in \mathcal {CPP}$
whose four regular subspaces are rescalings of the
![]() $\left \{ J_{i}\right \}. $
Let
$\left \{ J_{i}\right \}. $
Let
![]() $\left \{ h_{i}\right \} _{i=1}^{4}=RK(H)$
, and for
$\left \{ h_{i}\right \} _{i=1}^{4}=RK(H)$
, and for
![]() $r=1,...,4$
, let
$r=1,...,4$
, let
![]() $\left \{ j_{rs}\right \} _{s=1}^{3}=RK(J_{r}).$
The chart below gives the numbering scheme for the supposed rescalings and notation for certain values of
$\left \{ j_{rs}\right \} _{s=1}^{3}=RK(J_{r}).$
The chart below gives the numbering scheme for the supposed rescalings and notation for certain values of
![]() $\operatorname *{kos}.$
For instance, the first row indicates that rescaling takes the three kernel functions of
$\operatorname *{kos}.$
For instance, the first row indicates that rescaling takes the three kernel functions of
![]() $J_{1}$
, in the indicated order, to the indicated kernel functions of H. The last entry of the line introduces notation. The other lines are similar. We will not need to consider the values of
$J_{1}$
, in the indicated order, to the indicated kernel functions of H. The last entry of the line introduces notation. The other lines are similar. We will not need to consider the values of
![]() $\operatorname *{kos}$
associated with the last row.
$\operatorname *{kos}$
associated with the last row.
 $$\begin{align*}\begin{array}{lllllll}J_{1}\! & j_{11},j_{12},j_{13} & \rightarrow & h_{1},h_{2},h_{3}, &L_{23} & = &\operatorname*{kos}_{j_{11}}(j_{12},j_{13}),\\J_{2} & j_{21},j_{22},j_{23} & \rightarrow & h_{1},h_{3},h_{4}, &L_{34} & = & \operatorname*{kos}_{j_{21}}(j_{22},j_{23}),\\J_{3} &j_{31},j_{32},j_{33} & \rightarrow & h_{1},h_{4},h_{2}, & L_{42} & = & \operatorname*{kos}_{j_{31}}(j_{32},j_{33}),\\J_{4} & j_{41},j_{42},j_{43} & \rightarrow & h_{2},h_{3},h_{4}. & &&\end{array} \end{align*}$$
$$\begin{align*}\begin{array}{lllllll}J_{1}\! & j_{11},j_{12},j_{13} & \rightarrow & h_{1},h_{2},h_{3}, &L_{23} & = &\operatorname*{kos}_{j_{11}}(j_{12},j_{13}),\\J_{2} & j_{21},j_{22},j_{23} & \rightarrow & h_{1},h_{3},h_{4}, &L_{34} & = & \operatorname*{kos}_{j_{21}}(j_{22},j_{23}),\\J_{3} &j_{31},j_{32},j_{33} & \rightarrow & h_{1},h_{4},h_{2}, & L_{42} & = & \operatorname*{kos}_{j_{31}}(j_{32},j_{33}),\\J_{4} & j_{41},j_{42},j_{43} & \rightarrow & h_{2},h_{3},h_{4}. & &&\end{array} \end{align*}$$
The required coherence is that when rescaled images overlap, they must be compatible; so, for instance, we must have
![]() $\delta (j_{11},j_{13} )=\delta (j_{21},j_{22})$
because both pairs are mapped to
$\delta (j_{11},j_{13} )=\delta (j_{21},j_{22})$
because both pairs are mapped to
![]() $(h_{1},h_{3}).$
$(h_{1},h_{3}).$
Define
![]() $\mathcal {M}(\left \{ J_{i}\right \} )$
by
$\mathcal {M}(\left \{ J_{i}\right \} )$
by
 $$ \begin{align} \mathcal{M}(\left\{ J_{i}\right\} )= \begin{pmatrix} 1 & L_{23} & L_{24}\\ L_{32} & 1 & L_{34}\\ L_{42} & L_{43} & 1 \end{pmatrix}. \end{align} $$
$$ \begin{align} \mathcal{M}(\left\{ J_{i}\right\} )= \begin{pmatrix} 1 & L_{23} & L_{24}\\ L_{32} & 1 & L_{34}\\ L_{42} & L_{43} & 1 \end{pmatrix}. \end{align} $$
The upper-right entries in this matrix are defined in the previous display. The lower-left entries are their complex conjugates. If there is an H, then this matrix will equal
![]() $\operatorname *{KOS}(H,1)$
.
$\operatorname *{KOS}(H,1)$
.
Because
![]() $\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {CPP}$
, we know from Theorem 3.1 that each
$\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {CPP}$
, we know from Theorem 3.1 that each
![]() $\left \vert L_{ij}\right \vert \leq 1.$
Hence, Lemma 6.1 can be applied and that gives several conditions equivalent to
$\left \vert L_{ij}\right \vert \leq 1.$
Hence, Lemma 6.1 can be applied and that gives several conditions equivalent to
![]() $\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0$
including
$\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0$
including
![]() $\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0$
and the analog of (6.2). We can now translate Theorem 6.2 to this context.
$\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0$
and the analog of (6.2). We can now translate Theorem 6.2 to this context.
Theorem 6.4 Given
![]() $\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {CPP}$
and
$\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {CPP}$
and
![]() $\left \{ J_{i}\right \} _{i=1}^{4}\rightrightarrows \,??$
, there is a four-dimensional
$\left \{ J_{i}\right \} _{i=1}^{4}\rightrightarrows \,??$
, there is a four-dimensional
![]() $H\in \mathcal {CPP}$
with
$H\in \mathcal {CPP}$
with
![]() $\left \{ J_{i}\right \} _{i=2} ^{4}\rightrightarrows \,H$
if and only if
$\left \{ J_{i}\right \} _{i=2} ^{4}\rightrightarrows \,H$
if and only if
![]() $\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0,$
or, equivalently
$\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0,$
or, equivalently
![]() $\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0,$
or, equivalently, the numbers
$\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0,$
or, equivalently, the numbers
![]() $\left \{ L_{ij}\right \} _{i,j=2,3,4}$
satisfy the analog of (6.2).
$\left \{ L_{ij}\right \} _{i,j=2,3,4}$
satisfy the analog of (6.2).
(If we only knew that
![]() $\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {RK}$
, then deriving
$\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {RK}$
, then deriving
![]() $\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0$
from
$\mathcal {M}(\left \{ J_{i}\right \} )\succcurlyeq 0$
from
![]() $\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0$
requires the additional assumption that the
$\det \mathcal {M}(\left \{ J_{i}\right \} )\geq 0$
requires the additional assumption that the
![]() $\left \vert L_{ij}\right \vert \leq 1.$
However, this is not actually a different formulation. By Theorem 3.1, adding the assumptions that
$\left \vert L_{ij}\right \vert \leq 1.$
However, this is not actually a different formulation. By Theorem 3.1, adding the assumptions that
![]() $\left \vert L_{ij}\right \vert \leq 1$
is equivalent to passing from the assumption that
$\left \vert L_{ij}\right \vert \leq 1$
is equivalent to passing from the assumption that
![]() $\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {RK}$
to the assumption that
$\left \{ J_{i}\right \} _{i=2}^{4}\subset \mathcal {RK}$
to the assumption that
![]() $\left \{ J_{i}\right \} _{i=2} ^{4}\subset \mathcal {CPP}$
.)
$\left \{ J_{i}\right \} _{i=2} ^{4}\subset \mathcal {CPP}$
.)
6.3 Quiggin’s example
There is a simple criterion for determining if a three-dimensional
![]() $H\in $
$H\in $
![]() $\mathcal {RK}$
is in
$\mathcal {RK}$
is in
![]() $\mathcal {CPP}$
. From Theorem 3.1, we see that
$\mathcal {CPP}$
. From Theorem 3.1, we see that
![]() $H\in \mathcal {CPP}$
if and only if
$H\in \mathcal {CPP}$
if and only if
![]() $\left \vert \operatorname *{kos} _{1}(2,3)\right \vert \leq 1.$
The analogous question for four-dimensional H is more complicated. It is clearly necessary that each regular three-dimensional subspace of H be in
$\left \vert \operatorname *{kos} _{1}(2,3)\right \vert \leq 1.$
The analogous question for four-dimensional H is more complicated. It is clearly necessary that each regular three-dimensional subspace of H be in
![]() $\mathcal {CPP}$
, but knowing if that condition is sufficient is essentially Question 2 of the introduction. The first example showing the condition is not sufficient is due to Quiggin [Reference Raghupathi and PaulsenQ], [Reference Agler and PickAM, p. 94]. He constructed a family
$\mathcal {CPP}$
, but knowing if that condition is sufficient is essentially Question 2 of the introduction. The first example showing the condition is not sufficient is due to Quiggin [Reference Raghupathi and PaulsenQ], [Reference Agler and PickAM, p. 94]. He constructed a family
![]() $H_{x}$
,
$H_{x}$
,
![]() $0<x<1$
of spaces
$0<x<1$
of spaces
![]() $H_{x}$
in
$H_{x}$
in
![]() $\mathcal {RK}$
each having the Pick property, a weaker statement than the CPP and which we will not detail here, and showed that
$\mathcal {RK}$
each having the Pick property, a weaker statement than the CPP and which we will not detail here, and showed that
![]() $H_{1/4}\notin \ \mathcal {CPP}$
. Here, we will use the results of the previous sections to read off directly the facts that for each
$H_{1/4}\notin \ \mathcal {CPP}$
. Here, we will use the results of the previous sections to read off directly the facts that for each
![]() $0<x<1$
the regular subspaces of
$0<x<1$
the regular subspaces of
![]() $H_{x}$
have the CPP but
$H_{x}$
have the CPP but
![]() $H_{x}$
does not.
$H_{x}$
does not.
Following Quiggin, we introduce a family
![]() $\left \{ H_{x}:0<x<1\right \} \subset \mathcal {RK}$
of four-dimensional spaces by specifying their Gram matrices,
$\left \{ H_{x}:0<x<1\right \} \subset \mathcal {RK}$
of four-dimensional spaces by specifying their Gram matrices,
![]() $\operatorname *{Gr}(H_{x}).$
For
$\operatorname *{Gr}(H_{x}).$
For
![]() $0<x<1$
and
$0<x<1$
and
![]() $s=(1-x)\sqrt {x}$
, set
$s=(1-x)\sqrt {x}$
, set
 $$\begin{align*}\operatorname*{Gr}(H_{x})= \begin{pmatrix} 1 & x & x & x+is\\ x & 1 & x-is & x\\ x & x+is & 1 & x\\ x-is & x & x & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\operatorname*{Gr}(H_{x})= \begin{pmatrix} 1 & x & x & x+is\\ x & 1 & x-is & x\\ x & x+is & 1 & x\\ x-is & x & x & 1 \end{pmatrix}. \end{align*}$$
To show this is the Gram matrix of an
![]() $\mathcal {RK}$
, we need to show that
$\mathcal {RK}$
, we need to show that
![]() $\operatorname *{Gr}(H_{x})\succ 0.$
By Lemma 5.5, we can do that by checking the signs of the leading principal minors. They are
$\operatorname *{Gr}(H_{x})\succ 0.$
By Lemma 5.5, we can do that by checking the signs of the leading principal minors. They are
and, by inspection, are all positive for
![]() $0<x<1$
. (Those computations and the determinant computations below were done using computer algebra.)
$0<x<1$
. (Those computations and the determinant computations below were done using computer algebra.)
Earlier we used the matrices
![]() $\operatorname *{KOS}(\operatorname *{Gr} (H_{x}),1)$
from (6.5). Here, for ease in computing, we use the matrices
$\operatorname *{KOS}(\operatorname *{Gr} (H_{x}),1)$
from (6.5). Here, for ease in computing, we use the matrices
![]() $\operatorname *{MQ}(H_{x},1)= \ \left ( \delta _{1i}\delta _{1j} \operatorname *{kos}\nolimits _{1}(i,j)\right ) _{i,j=2}^{4}$
mentioned in (2.16). The two have determinants of the same sign as do their square submatrices.
$\operatorname *{MQ}(H_{x},1)= \ \left ( \delta _{1i}\delta _{1j} \operatorname *{kos}\nolimits _{1}(i,j)\right ) _{i,j=2}^{4}$
mentioned in (2.16). The two have determinants of the same sign as do their square submatrices.
From the definitions, we have
 $$\begin{align*}\operatorname*{MQ}(H_{x},1)= \begin{pmatrix} 1-x^{2} & 1-\frac{x^{2}}{x-is} & 1-x-is\\ 1-\frac{x^{2}}{x+is} & 1-x^{2} & 1-x-is\\ 1-x+is & 1-x+is & \left( 1-x\right) (1+x^{2}) \end{pmatrix}. \end{align*}$$
$$\begin{align*}\operatorname*{MQ}(H_{x},1)= \begin{pmatrix} 1-x^{2} & 1-\frac{x^{2}}{x-is} & 1-x-is\\ 1-\frac{x^{2}}{x+is} & 1-x^{2} & 1-x-is\\ 1-x+is & 1-x+is & \left( 1-x\right) (1+x^{2}) \end{pmatrix}. \end{align*}$$
Fix
![]() $x.$
We want to know that
$x.$
We want to know that
![]() $\left \{ J_{xi}\right \} _{1}^{4},$
the regular three-dimensional subspaces of
$\left \{ J_{xi}\right \} _{1}^{4},$
the regular three-dimensional subspaces of
![]() $H_{x},$
have the CPP. By (5) of Theorem 3.1, we know that
$H_{x},$
have the CPP. By (5) of Theorem 3.1, we know that
![]() $J_{x2}\in \mathcal {CPP}$
if the matrix
$J_{x2}\in \mathcal {CPP}$
if the matrix
![]() $\mathcal {J}_{2}$
obtained by deleting the first row and first column of
$\mathcal {J}_{2}$
obtained by deleting the first row and first column of
![]() $\operatorname *{MQ}(H_{x},1)$
satisfies
$\operatorname *{MQ}(H_{x},1)$
satisfies
![]() $\mathcal {J}_{2}\succcurlyeq 0$
. That will follow if we show
$\mathcal {J}_{2}\succcurlyeq 0$
. That will follow if we show
![]() $\det \mathcal {J}_{2}\geq 0.$
Similarly for
$\det \mathcal {J}_{2}\geq 0.$
Similarly for
![]() $J_{x3}$
and
$J_{x3}$
and
![]() $J_{x4}$
. For
$J_{x4}$
. For
![]() $J_{x1}$
, we follow the same path but starting with
$J_{x1}$
, we follow the same path but starting with
![]() $\operatorname *{MQ}(H_{x},2)$
rather than
$\operatorname *{MQ}(H_{x},2)$
rather than
![]() $\operatorname *{MQ}(H_{x},1).$
To show that
$\operatorname *{MQ}(H_{x},1).$
To show that
![]() $H_{x}\notin \mathcal {CPP}$
, we will show that
$H_{x}\notin \mathcal {CPP}$
, we will show that
![]() $\det \operatorname *{MQ} (H_{x},1)<0$
and hence
$\det \operatorname *{MQ} (H_{x},1)<0$
and hence
![]() $\operatorname *{MQ}(H_{x},1)\succcurlyeq 0$
fails. All these things can be seen in the explicit formulas for the determinants. Note that for
$\operatorname *{MQ}(H_{x},1)\succcurlyeq 0$
fails. All these things can be seen in the explicit formulas for the determinants. Note that for
![]() $0<x<1,$
we have
$0<x<1,$
we have
![]() $x^{2}-x+1>0.$
We have
$x^{2}-x+1>0.$
We have
 $$ \begin{align*} \det\mathcal{J}_{1} & =\det\mathcal{J}_{2}=\det\mathcal{J}_{3}=x^{2}\left( x+1\right) \left( x-1\right) ^{2},\\ \det\mathcal{J}_{4} & =\frac{x^{3}\left( x+1\right) \left( x-1\right) ^{2}}{x^{2}-x+1},\\ \det\operatorname*{MQ}(H_{x},1) & =\frac{\left( \begin{array} [c]{c} 2s^{4}x^{2}-s^{2}x^{7}+s^{2}x^{6}+s^{2}x^{5}+3s^{2}x^{4}\\ -4s^{2}x^{3}-x^{9}+x^{8}+2x^{7}-2x^{6}-x^{5}+x^{4} \end{array} \right) }{s^{2}+x^{2}}\\ & =-\frac{x^{3}\left( x+1\right) ^{2}\left( x-1\right) ^{4}}{x^{2}-x+1}. \end{align*} $$
$$ \begin{align*} \det\mathcal{J}_{1} & =\det\mathcal{J}_{2}=\det\mathcal{J}_{3}=x^{2}\left( x+1\right) \left( x-1\right) ^{2},\\ \det\mathcal{J}_{4} & =\frac{x^{3}\left( x+1\right) \left( x-1\right) ^{2}}{x^{2}-x+1},\\ \det\operatorname*{MQ}(H_{x},1) & =\frac{\left( \begin{array} [c]{c} 2s^{4}x^{2}-s^{2}x^{7}+s^{2}x^{6}+s^{2}x^{5}+3s^{2}x^{4}\\ -4s^{2}x^{3}-x^{9}+x^{8}+2x^{7}-2x^{6}-x^{5}+x^{4} \end{array} \right) }{s^{2}+x^{2}}\\ & =-\frac{x^{3}\left( x+1\right) ^{2}\left( x-1\right) ^{4}}{x^{2}-x+1}. \end{align*} $$
This shows that the matching distances property together with the cocycle property are not sufficient to insure that a set of four three-dimensional spaces with the CPP can be assembled into a four-dimensional space with the CPP. For
![]() $x=1/4$
, the following result is due to Quiggin [Reference Raghupathi and PaulsenQ], [Reference Agler and PickAM].
$x=1/4$
, the following result is due to Quiggin [Reference Raghupathi and PaulsenQ], [Reference Agler and PickAM].
Proposition 6.5 Fix x,
![]() $0<x<1,$
and let
$0<x<1,$
and let
![]() $\left \{ J_{xi}\right \} _{i=1}^{4}$
be the three-dimensional regular subspaces of
$\left \{ J_{xi}\right \} _{i=1}^{4}$
be the three-dimensional regular subspaces of
![]() $H_{x}$
. Then:
$H_{x}$
. Then:
-
(1) The
 $\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
and
$\left \{ J_{i}\right \} _{i=1}^{4}\subset \mathcal {CPP}$
and
 $\left \{ J_{i}\right \} _{i=1}^{4}\rightrightarrows \,??$
.
$\left \{ J_{i}\right \} _{i=1}^{4}\rightrightarrows \,??$
. -
(2) There is an
 $H\in \mathcal {RK}$
with
$H\in \mathcal {RK}$
with
 $\left \{ J_{i}\right \} _{i=1} ^{4}\rightrightarrows H$
.
$\left \{ J_{i}\right \} _{i=1} ^{4}\rightrightarrows H$
. -
(3) There is no
 $H\in \mathcal {CPP}$
with
$H\in \mathcal {CPP}$
with
 $\left \{ J_{i}\right \} _{i=1} ^{4}\rightrightarrows H$
.
$\left \{ J_{i}\right \} _{i=1} ^{4}\rightrightarrows H$
.
Proof We verified above that the
![]() $\left \{ J_{i}\right \} $
all have the CPP. The coherence is automatic because the
$\left \{ J_{i}\right \} $
all have the CPP. The coherence is automatic because the
![]() $\left \{ J_{i}\right \} $
are the three-dimensional regular subspaces of a four-dimensional
$\left \{ J_{i}\right \} $
are the three-dimensional regular subspaces of a four-dimensional
![]() $\mathcal {RK}$
. The second statement is automatic;
$\mathcal {RK}$
. The second statement is automatic;
![]() $H=H_{x}$
will suffice. It is included to emphasize that there is no obstruction to assembling the
$H=H_{x}$
will suffice. It is included to emphasize that there is no obstruction to assembling the
![]() $\left \{ J_{i}\right \} $
into an
$\left \{ J_{i}\right \} $
into an
![]() $H\in \mathcal {RK},$
just not an
$H\in \mathcal {RK},$
just not an
![]() $H\in \mathcal {CPP}$
.
$H\in \mathcal {CPP}$
.
6.4 Tetrahedra in
 $\mathbb {RH}^{k}$
$\mathbb {RH}^{k}$
6.4.1 Preliminaries
In this section, we specialize the previous results to real hyperbolic triangles and tetrahedra, those sitting in some
![]() $\mathbb {RH}^{k},$
or, equivalently, inside a copy of
$\mathbb {RH}^{k},$
or, equivalently, inside a copy of
![]() $\mathbb {RH}^{k}$
inside some
$\mathbb {RH}^{k}$
inside some
![]() $\mathbb {CH} ^{n}.$
The study of polyhedra in
$\mathbb {CH} ^{n}.$
The study of polyhedra in
![]() $\mathbb {RH}^{k}$
is an active research topic with a rich history; references include the books [Reference AndersonAn, Reference FenchelF, Reference GoldmanGo], surveys [Reference JansonJ, Reference Mednykh and PashkevichMP], and research papers [Reference DíazDi, Reference Hodgson and RivinHR, Reference WeeksW]. Also, there is some study of the relation between RKHSs and sets in
$\mathbb {RH}^{k}$
is an active research topic with a rich history; references include the books [Reference AndersonAn, Reference FenchelF, Reference GoldmanGo], surveys [Reference JansonJ, Reference Mednykh and PashkevichMP], and research papers [Reference DíazDi, Reference Hodgson and RivinHR, Reference WeeksW]. Also, there is some study of the relation between RKHSs and sets in
![]() $\mathbb {RH}^{k}$
([Reference Burger and IzzoBIM, Reference RochbergRo, Sec. 7]). Some of the results below are in those references or can be developed efficiently using those techniques. Our goal here is to show how results for real hyperbolic tetrahedra can be seen as specialization of results for complex hyperbolic tetrahedra.
$\mathbb {RH}^{k}$
([Reference Burger and IzzoBIM, Reference RochbergRo, Sec. 7]). Some of the results below are in those references or can be developed efficiently using those techniques. Our goal here is to show how results for real hyperbolic tetrahedra can be seen as specialization of results for complex hyperbolic tetrahedra.
The following simple consequence of Lemma 2.1 of [Reference Burger, Iozzi and MonodBI] lets us tell when
![]() $X\subset \mathbb {CH}^{n}$
is actually in a copy of
$X\subset \mathbb {CH}^{n}$
is actually in a copy of
![]() $\mathbb {RH}^{n}.$
$\mathbb {RH}^{n}.$
Proposition 6.6
![]() $X=\left \{ x_{i}\right \} _{i=1}^{s}\subset \mathbb {CH}^{n}$
is inside a copy of
$X=\left \{ x_{i}\right \} _{i=1}^{s}\subset \mathbb {CH}^{n}$
is inside a copy of
![]() $\mathbb {RH}^{s-1}\subset \mathbb {CH}^{n}$
if and only if all the numbers
$\mathbb {RH}^{s-1}\subset \mathbb {CH}^{n}$
if and only if all the numbers
![]() $\operatorname *{kos}_{i}(p,q)$
are real, or, equivalently, if and only if the entries of the Gram matrix of
$\operatorname *{kos}_{i}(p,q)$
are real, or, equivalently, if and only if the entries of the Gram matrix of
![]() $DA(X)$
are real.
$DA(X)$
are real.
Hence, the results in this section also apply to Hilbert spaces
![]() $H\in \mathcal {CPP}$
which are rescalings of spaces with real Gram matrices. Those spaces are the finite-dimensional regular subspaces of the diameter spaces discussed in [Reference Arcozzi, Rochberg, Sawyer and JaroszARS].
$H\in \mathcal {CPP}$
which are rescalings of spaces with real Gram matrices. Those spaces are the finite-dimensional regular subspaces of the diameter spaces discussed in [Reference Arcozzi, Rochberg, Sawyer and JaroszARS].
Given
![]() $\left \{ x_{1},x_{2},x_{3}\right \} \subset \mathbb {RH}^{k}$
, we denote the vertex angle between geodesics
$\left \{ x_{1},x_{2},x_{3}\right \} \subset \mathbb {RH}^{k}$
, we denote the vertex angle between geodesics
![]() $x_{1}x_{2}$
and
$x_{1}x_{2}$
and
![]() $x_{1}x_{3}.$
by
$x_{1}x_{3}.$
by
![]() $va_{23}.$
$va_{23}.$
Corollary 6.7 The triangle
![]() $T=\left \{ x_{1},x_{2},x_{3}\right \} \subset \mathbb {CH}^{n}$
is in a copy of
$T=\left \{ x_{1},x_{2},x_{3}\right \} \subset \mathbb {CH}^{n}$
is in a copy of
![]() $\mathbb {RH}^{2}$
if and only if
$\mathbb {RH}^{2}$
if and only if
![]() $\operatorname *{kos}_{1}(2,3)$
is real. In that case,
$\operatorname *{kos}_{1}(2,3)$
is real. In that case,
![]() $\operatorname *{kos} _{1}(2,3)=\cos va_{23}$
.
$\operatorname *{kos} _{1}(2,3)=\cos va_{23}$
.
Proof Using the model triangle
![]() $\Gamma $
in (3.1), it is easy to check that if
$\Gamma $
in (3.1), it is easy to check that if
![]() $\operatorname *{kos}_{1}(2,3)$
is real, then the coordinates of the points of
$\operatorname *{kos}_{1}(2,3)$
is real, then the coordinates of the points of
![]() $\Gamma $
are real and hence also so are the other values of
$\Gamma $
are real and hence also so are the other values of
![]() $\operatorname *{kos}.$
It then follows from the previous proposition that T is in a copy of
$\operatorname *{kos}.$
It then follows from the previous proposition that T is in a copy of
![]() $\mathbb {RH}^{k}.$
Because
$\mathbb {RH}^{k}.$
Because
![]() $\Gamma $
only has three points, we can take
$\Gamma $
only has three points, we can take
![]() $k=2.$
Using (2.14), we see that
$k=2.$
Using (2.14), we see that
![]() $\operatorname *{kos} _{1}(2,3)=\left \langle \left \langle \widehat {x_{2}},\widehat {x_{3} }\right \rangle \right \rangle .$
That inner product equals the cosine of the Euclidean angle at the origin of
$\operatorname *{kos} _{1}(2,3)=\left \langle \left \langle \widehat {x_{2}},\widehat {x_{3} }\right \rangle \right \rangle .$
That inner product equals the cosine of the Euclidean angle at the origin of
![]() $\mathbb {R}^{2}$
between the segments
$\mathbb {R}^{2}$
between the segments
![]() $0\widehat {x_{2}}$
and
$0\widehat {x_{2}}$
and
![]() $0\widehat {x_{3}}$
. On T, the Euclidean metric on
$0\widehat {x_{3}}$
. On T, the Euclidean metric on
![]() $\mathbb {R}^{2}$
is conformal with the hyperbolic metric, and hence the Euclidean angle whose cosine we found is also the hyperbolic angle.
$\mathbb {R}^{2}$
is conformal with the hyperbolic metric, and hence the Euclidean angle whose cosine we found is also the hyperbolic angle.
If triangles can be assembled into a real hyperbolic tetrahedron, then it can be done in
![]() $\mathbb {RH}^{3}.$
The model we will use for
$\mathbb {RH}^{3}.$
The model we will use for
![]() $\mathbb {RH}^{3}$
is the unit ball in
$\mathbb {RH}^{3}$
is the unit ball in
![]() $\mathbb {R}^{3}$
with the Poincare metric. We write
$\mathbb {R}^{3}$
with the Poincare metric. We write
![]() $\mathbb {S}_{2}$
for the unit sphere in
$\mathbb {S}_{2}$
for the unit sphere in
![]() $\mathbb {R}^{3}.$
$\mathbb {R}^{3}.$
Because the Poincare ball model for
![]() $\mathbb {RH}^{3}$
is conformal with Euclidean space, some of our results here also apply to structures in Euclidean space. For instance, the condition of vertex angles on the bivalent vertices that are necessary to form a trivalent vertex is the same in both cases.
$\mathbb {RH}^{3}$
is conformal with Euclidean space, some of our results here also apply to structures in Euclidean space. For instance, the condition of vertex angles on the bivalent vertices that are necessary to form a trivalent vertex is the same in both cases.
If we start with four real hyperbolic triangles which satisfy the matching side conditions necessary for assembly into a tetrahedron X, then Theorem 6.2 gives conditions for there to be an
![]() $X$
in terms of a matrix
$X$
in terms of a matrix
![]() $\mathcal {M}(X)$
whose entries are values of
$\mathcal {M}(X)$
whose entries are values of
![]() $\operatorname *{kos}.$
Because we are in real hyperbolic space, those values are cosines of vertex angles. To emphasize this, we introduce name and notation for that type of
$\operatorname *{kos}.$
Because we are in real hyperbolic space, those values are cosines of vertex angles. To emphasize this, we introduce name and notation for that type of
![]() $\mathcal {M} (X):$
$\mathcal {M} (X):$
 $$ \begin{align} \mathcal{M}_{CVA}(X)= \begin{pmatrix} 1 & \cos va_{23} & \cos va_{24}\\ \cos va_{32} & 1 & \cos va_{34}\\ \cos va_{42} & \cos va_{43} & 1 \end{pmatrix} \end{align} $$
$$ \begin{align} \mathcal{M}_{CVA}(X)= \begin{pmatrix} 1 & \cos va_{23} & \cos va_{24}\\ \cos va_{32} & 1 & \cos va_{34}\\ \cos va_{42} & \cos va_{43} & 1 \end{pmatrix} \end{align} $$
with the subscript
![]() $CVA$
referring to the fact the entries are cosines of vertex angles. Theorem 6.2 specializes as the following.
$CVA$
referring to the fact the entries are cosines of vertex angles. Theorem 6.2 specializes as the following.
Theorem 6.8 Given triangles
![]() $\left \{ T_{i}\right \} _{i=1}^{4}$
in
$\left \{ T_{i}\right \} _{i=1}^{4}$
in
![]() $\mathbb {RH}^{n}$
with
$\mathbb {RH}^{n}$
with
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
, there is a tetrahedron X in
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
, there is a tetrahedron X in
![]() $\mathbb {RH}^{n}$
such that
$\mathbb {RH}^{n}$
such that
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
if and only if
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
if and only if
![]() $\det \mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})\geq 0.$
$\det \mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})\geq 0.$
6.4.2 The triangle inequality for angles
We saw conditions for three bivalent vertices in
![]() $\mathbb {CH}^{n}$
to be assembled into a trivalent vertex. Those conditions specialize to vertices in
$\mathbb {CH}^{n}$
to be assembled into a trivalent vertex. Those conditions specialize to vertices in
![]() $\mathbb {RH}^{n}$
and, because the geometry of our model of
$\mathbb {RH}^{n}$
and, because the geometry of our model of
![]() $\mathbb {RH}^{n}$
is conformal with Euclidean geometry, the same conditions apply to vertices in Euclidean space. The question of when three bivalent vertices in
$\mathbb {RH}^{n}$
is conformal with Euclidean geometry, the same conditions apply to vertices in Euclidean space. The question of when three bivalent vertices in
![]() $\mathbb {R}^{3}$
can be assembled into a trivalent vertex is a straightforward question in Euclidean solid geometry and it is not surprising that it has a simple answer. We now look at that briefly.
$\mathbb {R}^{3}$
can be assembled into a trivalent vertex is a straightforward question in Euclidean solid geometry and it is not surprising that it has a simple answer. We now look at that briefly.
Corollary 6.9 (The triangle inequality for angles)
The numbers
![]() $0\leq \alpha ,\beta ,\gamma \leq \pi $
are the (real hyperbolic or Euclidean) angles of a trivalent vertex in (real hyperbolic or Euclidean) space if and only if
$0\leq \alpha ,\beta ,\gamma \leq \pi $
are the (real hyperbolic or Euclidean) angles of a trivalent vertex in (real hyperbolic or Euclidean) space if and only if
![]() $\alpha \leq \beta +\gamma .$
$\alpha \leq \beta +\gamma .$
Proof There is such a vertex if and only if the vertex can be realized as part of a real hyperbolic tetrahedron
![]() $X.$
By the previous theorem, that can happen if and only if the matrix
$X.$
By the previous theorem, that can happen if and only if the matrix
![]() $\mathcal {M}_{CVA}(X)$
of (6.6) has a positive determinant. We use Lemma 6.1 to rewrite that determinant condition, and then we compute
$\mathcal {M}_{CVA}(X)$
of (6.6) has a positive determinant. We use Lemma 6.1 to rewrite that determinant condition, and then we compute
 $$ \begin{align} (\cos\alpha-\cos\beta\cos\gamma)^{2} & \leq(1-\cos^{2}\beta)(1-\cos ^{2}\gamma),\\ \left\vert \cos\alpha-\cos\beta\cos\gamma\right\vert & \leq\sin\beta \sin\gamma,\nonumber\\ -\sin\beta\sin\gamma+\cos\beta\cos\gamma & \leq\cos\alpha\leq\sin\beta \sin\gamma+\cos\beta\cos\gamma,\nonumber \end{align} $$
$$ \begin{align} (\cos\alpha-\cos\beta\cos\gamma)^{2} & \leq(1-\cos^{2}\beta)(1-\cos ^{2}\gamma),\\ \left\vert \cos\alpha-\cos\beta\cos\gamma\right\vert & \leq\sin\beta \sin\gamma,\nonumber\\ -\sin\beta\sin\gamma+\cos\beta\cos\gamma & \leq\cos\alpha\leq\sin\beta \sin\gamma+\cos\beta\cos\gamma,\nonumber \end{align} $$
If
![]() $\gamma +\beta <\pi $
, then the three angles in the previous line are in the range
$\gamma +\beta <\pi $
, then the three angles in the previous line are in the range
![]() $\left ( 0,\pi \right ) $
where the cosine is monotone decreasing. In that case, the first inequality gives
$\left ( 0,\pi \right ) $
where the cosine is monotone decreasing. In that case, the first inequality gives
![]() $\alpha \leq \beta +\gamma .$
In the other case, we have
$\alpha \leq \beta +\gamma .$
In the other case, we have
![]() $\alpha \leq \pi \leq \beta +\gamma .$
In both cases, we have the desired inequality. The argument is reversible.
$\alpha \leq \pi \leq \beta +\gamma .$
In both cases, we have the desired inequality. The argument is reversible.
In Section 6.4, we will present the triangle for which the previous corollary is a “triangle inequality.”
There is an interesting identity that can be used to give an alternate proof of the corollary. Set
![]() $s=(\alpha +\beta +\gamma )/2.$
By trigonometric analysis [Co, Reference JansonJ] or, as Roeder notes in [Reference RoederRoe], by computation with complex exponentials, we have
$s=(\alpha +\beta +\gamma )/2.$
By trigonometric analysis [Co, Reference JansonJ] or, as Roeder notes in [Reference RoederRoe], by computation with complex exponentials, we have
If we know
![]() $\det \mathcal {M}_{CVA}(X)\geq 0$
, then an analysis of cases shows that all the factors on the right side are nonnegative. Knowing that gives the conclusion of the corollary.
$\det \mathcal {M}_{CVA}(X)\geq 0$
, then an analysis of cases shows that all the factors on the right side are nonnegative. Knowing that gives the conclusion of the corollary.
Finally, we have taken a long route to what is a rather obvious fact of solid geometry. Consider the task of building a model of a trivalent vertex from three wedges of paper. Certainly the job is impossible if one wedge is wider than the other two combined.
6.4.3 Dihedral angles
In real hyperbolic space, any three points sit in a totally geodesically embedded hyperbolic plane and hence each edge is in the intersection of two such planes. We define the dihedral angle at that edge to be the angle of intersection of the two planes. Thus, at each trivalent vertex, we have three vertex angles and three dihedral angles.
In fact, the dihedral angles are used more commonly than vertex angles in describing real hyperbolic polyhedra (see, for instance, [Reference Futer and GuéritaudFG, Reference Hodgson and RivinHR, Reference RoederRoe, Reference WeeksW] and the references therein). In this section and the next, we look briefly at the relation between the two types of angles and at how our earlier results translate to results involving dihedral angles. Some of the results we obtain are classical facts from solid geometry or spherical trigonometry. The work in this section is influenced by the work of Roeder in [Reference RoederRoe] and there are overlaps. We will be sketchy.
For the moment, we will use indices
![]() $r,s,t$
to denote three different indices from the set
$r,s,t$
to denote three different indices from the set
![]() $\left \{ 2,3,4\right \} .$
Given the tetrahedron
$\left \{ 2,3,4\right \} .$
Given the tetrahedron
![]() $X=\left \{ x_{1},x_{2},x_{3},x_{3}\right \} \subset \mathbb {RH}^{3}$
with
$X=\left \{ x_{1},x_{2},x_{3},x_{3}\right \} \subset \mathbb {RH}^{3}$
with
![]() $x_{1}$
at the origin, denote the triangular face with vertices
$x_{1}$
at the origin, denote the triangular face with vertices
![]() $\left \{ x_{1},x_{i} ,x_{j}\right \} $
by
$\left \{ x_{1},x_{i} ,x_{j}\right \} $
by
![]() $F_{ij}.$
The dihedral angle along edge s,
$F_{ij}.$
The dihedral angle along edge s,
![]() $s=2,3,4,$
is the angle
$s=2,3,4,$
is the angle
![]() $da_{rt}$
between the faces
$da_{rt}$
between the faces
![]() $F_{rs}$
and
$F_{rs}$
and
![]() $F_{st}.$
$F_{st}.$
As we mentioned, the angles in our ball model of
![]() $\mathbb {RH}^{3}$
agree with the Euclidean angles, and hence it suffices to do the Euclidean computation of the
$\mathbb {RH}^{3}$
agree with the Euclidean angles, and hence it suffices to do the Euclidean computation of the
![]() $da.$
To find
$da.$
To find
![]() $da_{rt}$
, we first find the inward pointing unit normals,
$da_{rt}$
, we first find the inward pointing unit normals,
![]() $n_{rs}$
for the face
$n_{rs}$
for the face
![]() $F_{rs},$
and similarly
$F_{rs},$
and similarly
![]() $n_{st},$
and then use the fact that
$n_{st},$
and then use the fact that
![]() $-\cos da_{rt}=\left \langle n_{rs},n_{st}\right \rangle .$
The requirement that
$-\cos da_{rt}=\left \langle n_{rs},n_{st}\right \rangle .$
The requirement that
![]() $n_{rs}$
be inward pointing is the requirement that
$n_{rs}$
be inward pointing is the requirement that
![]() $\left \langle n_{rs},x_{t}\right \rangle \geq 0.$
However, the formula for
$\left \langle n_{rs},x_{t}\right \rangle \geq 0.$
However, the formula for
![]() $da_{rt}$
is unchanged if the normals are replaced by their negatives, and hence it is enough to construct the normals so that the inner products
$da_{rt}$
is unchanged if the normals are replaced by their negatives, and hence it is enough to construct the normals so that the inner products
![]() $\left \langle n_{rs},x_{t}\right \rangle $
all have the same sign. Taking note of the fact that
$\left \langle n_{rs},x_{t}\right \rangle $
all have the same sign. Taking note of the fact that
![]() $\left \langle a,b\times c\right \rangle =\left \langle b,c\times a\right \rangle $
for vectors in
$\left \langle a,b\times c\right \rangle =\left \langle b,c\times a\right \rangle $
for vectors in
![]() $\mathbb {R}^{3}$
, we see that the choices
$\mathbb {R}^{3}$
, we see that the choices
![]() $\left \langle n_{rs},x_{t}\right \rangle $
$\left \langle n_{rs},x_{t}\right \rangle $
satisfy that requirement. Using these normals, we compute
 $$ \begin{align} \cos da_{s} & =-\,\left\langle \left\langle n_{rs},n_{st}\right\rangle \right\rangle\\& =-\left\langle \left\langle \frac{\widehat{x_{r}}\times\widehat{x_{s}} }{\left\Vert \widehat{x_{r}}\times\widehat{x_{s}}\right\Vert },\frac {\widehat{x_{s}}\times\widehat{x_{t}}}{\left\Vert \widehat{x_{s}} \times\widehat{x_{t}}\right\Vert }\right\rangle \right\rangle \nonumber\\ & =-\frac{\left\langle \left\langle \widehat{x_{r}},\widehat{x_{s} }\right\rangle \right\rangle \left\langle \left\langle \widehat{x_{s} },\widehat{x_{t}}\right\rangle \right\rangle -\left\langle \left\langle \widehat{x_{r}},\widehat{x_{t}}\right\rangle \right\rangle \left\langle \left\langle \widehat{x_{s}},\widehat{x_{s}}\right\rangle \right\rangle }{\left\Vert \widehat{x_{r}}\times\widehat{x_{s}}\right\Vert \left\Vert \widehat{x_{s}}\times\widehat{x_{t}}\right\Vert }\nonumber\\ & =\frac{\cos va_{rt}-\cos va_{rs}\cos va_{st}}{\sin va_{rs}\sin va_{st} }.\nonumber \end{align} $$
$$ \begin{align} \cos da_{s} & =-\,\left\langle \left\langle n_{rs},n_{st}\right\rangle \right\rangle\\& =-\left\langle \left\langle \frac{\widehat{x_{r}}\times\widehat{x_{s}} }{\left\Vert \widehat{x_{r}}\times\widehat{x_{s}}\right\Vert },\frac {\widehat{x_{s}}\times\widehat{x_{t}}}{\left\Vert \widehat{x_{s}} \times\widehat{x_{t}}\right\Vert }\right\rangle \right\rangle \nonumber\\ & =-\frac{\left\langle \left\langle \widehat{x_{r}},\widehat{x_{s} }\right\rangle \right\rangle \left\langle \left\langle \widehat{x_{s} },\widehat{x_{t}}\right\rangle \right\rangle -\left\langle \left\langle \widehat{x_{r}},\widehat{x_{t}}\right\rangle \right\rangle \left\langle \left\langle \widehat{x_{s}},\widehat{x_{s}}\right\rangle \right\rangle }{\left\Vert \widehat{x_{r}}\times\widehat{x_{s}}\right\Vert \left\Vert \widehat{x_{s}}\times\widehat{x_{t}}\right\Vert }\nonumber\\ & =\frac{\cos va_{rt}-\cos va_{rs}\cos va_{st}}{\sin va_{rs}\sin va_{st} }.\nonumber \end{align} $$
(Note that if the vertices are ordered, and hence the angles are signed, the cosine terms are independent of the ordering, but the sine factors are not. However, that product of sines is unchanged by reordering the vertices. The same comments apply to the expressions below.)
Definition 6.10 Suppose that for
![]() $2\leq i,j\leq 4$
, we are given angles
$2\leq i,j\leq 4$
, we are given angles
![]() $\left \{ va_{ij} \right \} $
and
$\left \{ va_{ij} \right \} $
and
![]() $\left \{ da_{ij}\right \} .$
For all i, we suppose
$\left \{ da_{ij}\right \} .$
For all i, we suppose
![]() $va_{ii}=0$
,
$va_{ii}=0$
,
![]() $da_{ii}=\pi \ and$
set
$da_{ii}=\pi \ and$
set
![]() $VA_{ii}=0$
,
$VA_{ii}=0$
,
![]() $DA_{ii}=\pi .$
For
$DA_{ii}=\pi .$
For
![]() $r\neq s$
, we define
$r\neq s$
, we define
Lemma 6.11 (Hyperbolic law of cosines)
If at the vertex point
![]() $x_{1}$
the tetrahedron
$x_{1}$
the tetrahedron
![]() $X=\left \{ x_{1}\right \} _{i=1}^{4}\subset \mathbb {RH}^{n}$
has vertex angles
$X=\left \{ x_{1}\right \} _{i=1}^{4}\subset \mathbb {RH}^{n}$
has vertex angles
![]() $\left \{ va_{ij}\right \} _{i,j=2}^{4}$
and dihedral angles
$\left \{ va_{ij}\right \} _{i,j=2}^{4}$
and dihedral angles
![]() $\left \{ da_{ij}\right \} _{i,j=2}^{4},$
then, with the notation (6.11) and (6.12),
$\left \{ da_{ij}\right \} _{i,j=2}^{4},$
then, with the notation (6.11) and (6.12),
We separated the definition from the lemma because we can use the definitions even if the
![]() $va_{ij}$
are not known to be data from a tetrahedron. If we have a set of triangles
$va_{ij}$
are not known to be data from a tetrahedron. If we have a set of triangles
![]() $\left \{ T_{i}\right \} _{i=2}^{4}$
in
$\left \{ T_{i}\right \} _{i=2}^{4}$
in
![]() $\mathbb {RH}^{k}$
which satisfy the coherence conditions for assembly into a tetrahedron,
$\mathbb {RH}^{k}$
which satisfy the coherence conditions for assembly into a tetrahedron,
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
, then we can construct the matrix
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
, then we can construct the matrix
![]() $\mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4}).$
Using that data in (6.11), we can compute imputed values of the
$\mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4}).$
Using that data in (6.11), we can compute imputed values of the
![]() $DA_{ij};$
the values
$DA_{ij};$
the values
![]() $\cos da_{ij}$
would have if assembly were possible. If
$\cos da_{ij}$
would have if assembly were possible. If
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
for a tetrahedron X, then those values will be cosines of dihedral angles and satisfy
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
for a tetrahedron X, then those values will be cosines of dihedral angles and satisfy
![]() $\left \vert D_{ij}\right \vert \leq 1.$
$\left \vert D_{ij}\right \vert \leq 1.$
Corollary 6.12 If
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
and
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows \,??$
and
![]() $DA_{ij}$
is computed using the
$DA_{ij}$
is computed using the
![]() $va_{ij}$
values from
$va_{ij}$
values from
![]() $\mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})$
and (6.11), then there is a tetrahedron X with
$\mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})$
and (6.11), then there is a tetrahedron X with
![]() $\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
if and only if for some
$\left \{ T_{i}\right \} _{i=2}^{4}\rightrightarrows X$
if and only if for some
![]() $i,j \ \left \vert DA_{ij}\right \vert \leq 1.$
$i,j \ \left \vert DA_{ij}\right \vert \leq 1.$
Informally, a value
![]() $\left \vert DA_{ij}\right \vert>1$
is not possible for any dihedral angle; hence, in that case, there is no tetrahedron.
$\left \vert DA_{ij}\right \vert>1$
is not possible for any dihedral angle; hence, in that case, there is no tetrahedron.
6.4.4 Spherical geometry
We can also use spherical geometry to relate the vertex angles and dihedral angles. Consider the tetrahedron
![]() $X=\left \{ 0,x_{2},x_{3}.x_{4}\right \} $
in
$X=\left \{ 0,x_{2},x_{3}.x_{4}\right \} $
in
![]() $\mathbb {RH}^{3}$
and the set
$\mathbb {RH}^{3}$
and the set
![]() $\widehat {X}=\left \{ \hat {x}_{2},\hat {x} _{3},\hat {x}_{4}\right \} $
in the boundary sphere
$\widehat {X}=\left \{ \hat {x}_{2},\hat {x} _{3},\hat {x}_{4}\right \} $
in the boundary sphere
![]() $\mathbb {S}_{2}.$
We regard
$\mathbb {S}_{2}.$
We regard
![]() $\widehat {X}$
as the set of vertices of a spherical triangle, also called
$\widehat {X}$
as the set of vertices of a spherical triangle, also called
![]() $\widehat {X}.$
$\widehat {X}.$
A fundamental relation between X and
![]() $\widehat {X}$
is that the side lengths and angle measures of
$\widehat {X}$
is that the side lengths and angle measures of
![]() $\widehat {X}$
are the sizes of the vertex angles and dihedral angles, respectively, of the trivalent vertex of X at the origin. (The analog for the Euclidean tetrahedron is perhaps visually clear.) Hence, in particular, the “Triangle Inequality for Angles,” Corollary 6.9, is literally the triangle inequality for the side lengths of the triangle
$\widehat {X}$
are the sizes of the vertex angles and dihedral angles, respectively, of the trivalent vertex of X at the origin. (The analog for the Euclidean tetrahedron is perhaps visually clear.) Hence, in particular, the “Triangle Inequality for Angles,” Corollary 6.9, is literally the triangle inequality for the side lengths of the triangle
![]() $\widehat {X}.$
$\widehat {X}.$
Associated with a spherical triangle with vertices
![]() $\widehat {X}=\left \{ \widehat {x_{2}},\widehat {x_{3}},\widehat {x_{4}}\right \} $
is its polar dual
$\widehat {X}=\left \{ \widehat {x_{2}},\widehat {x_{3}},\widehat {x_{4}}\right \} $
is its polar dual
![]() $\widehat {X}^{\#}.$
We forego the description of
$\widehat {X}^{\#}.$
We forego the description of
![]() $\widehat {X}^{\#}$
using spherical geometry and just note that it is the triangle with vertices
$\widehat {X}^{\#}$
using spherical geometry and just note that it is the triangle with vertices
![]() $\left \{ n_{34},n_{24},n_{23}\right \} $
given by the formula (6.9). It is straightforward to see that this is an actual duality;
$\left \{ n_{34},n_{24},n_{23}\right \} $
given by the formula (6.9). It is straightforward to see that this is an actual duality;
![]() $\widehat {X} ^{\#\#}=\widehat {X}.$
$\widehat {X} ^{\#\#}=\widehat {X}.$
The following is a fundamental relation between the geometries of a triangle and its polar dual.
Theorem 6.13 Suppose
![]() $\widehat {X}$
has angles
$\widehat {X}$
has angles
![]() $\left \{ a_{i}\right \} _{i=1,2,3}$
and side lengths
$\left \{ a_{i}\right \} _{i=1,2,3}$
and side lengths
![]() $\left \{ \ell _{i}\right \} _{i=1,2,3}$
and
$\left \{ \ell _{i}\right \} _{i=1,2,3}$
and
![]() $\widehat {X}^{\#}$
has angles
$\widehat {X}^{\#}$
has angles
![]() $\{a_{i}^{\#}\}_{i=1,2,3}$
and side lengths
$\{a_{i}^{\#}\}_{i=1,2,3}$
and side lengths
![]() $\{\ell _{i}^{\#}\}_{i=1,2,3}$
with all the lengths and angles selected between
$\{\ell _{i}^{\#}\}_{i=1,2,3}$
with all the lengths and angles selected between
![]() $0$
and
$0$
and
![]() $\pi ;$
then, for
$\pi ;$
then, for
![]() $i=1,2,3$
,
$i=1,2,3$
,
 $$ \begin{align*} \alpha_{i}^{\#} & =\pi-\ell_{i},\\ \ell_{i}^{\#} & =\pi-\alpha_{i}. \end{align*} $$
$$ \begin{align*} \alpha_{i}^{\#} & =\pi-\ell_{i},\\ \ell_{i}^{\#} & =\pi-\alpha_{i}. \end{align*} $$
We saw in Theorem 6.8 that angles
![]() $\left \{ va_{i}\right \} _{i=1,2,3}$
are the vertex angles of a trivalent vertex if and only if the matrix of their cosines,
$\left \{ va_{i}\right \} _{i=1,2,3}$
are the vertex angles of a trivalent vertex if and only if the matrix of their cosines,
![]() $\mathcal {M}_{CVA}(X)$
given by (6.6), satisfies
$\mathcal {M}_{CVA}(X)$
given by (6.6), satisfies
![]() $\det \mathcal {M}_{CVA}(X)\geq 0.$
Using Lemma 6.11, we can form the analogous result using negatives of cosines of dihedral angles. Set
$\det \mathcal {M}_{CVA}(X)\geq 0.$
Using Lemma 6.11, we can form the analogous result using negatives of cosines of dihedral angles. Set
 $$ \begin{align} \mathcal{M}_{-CDA}(X)= \begin{pmatrix} 1 & -\cos da_{23} & -\cos da_{24}\\ -\cos da_{32} & 1 & -\cos da_{34}\\ -\cos da_{42} & -\cos da_{43} & 1 \end{pmatrix}. \end{align} $$
$$ \begin{align} \mathcal{M}_{-CDA}(X)= \begin{pmatrix} 1 & -\cos da_{23} & -\cos da_{24}\\ -\cos da_{32} & 1 & -\cos da_{34}\\ -\cos da_{42} & -\cos da_{43} & 1 \end{pmatrix}. \end{align} $$
If we are given angles
![]() $\left \{ da_{ij}\right \} $
that are candidates for being the dihedral angles of a tetrahedron in
$\left \{ da_{ij}\right \} $
that are candidates for being the dihedral angles of a tetrahedron in
![]() $\mathbb {RH}^{3}$
, then we write
$\mathbb {RH}^{3}$
, then we write
![]() $\mathcal {M}_{-CDA}(?)$
for the matrix on the right-hand side of (6.13). Here is the analog of Theorem 6.2 for dihedral angles.
$\mathcal {M}_{-CDA}(?)$
for the matrix on the right-hand side of (6.13). Here is the analog of Theorem 6.2 for dihedral angles.
Theorem 6.14 Given a tetrahedron
![]() $X\subset \mathbb {RH}^{3}$
, we have
$X\subset \mathbb {RH}^{3}$
, we have
![]() $\det \mathcal {M} _{-CDA}(X)\geq 0.$
Conversely, if angles
$\det \mathcal {M} _{-CDA}(X)\geq 0.$
Conversely, if angles
![]() $\left \{ da_{ij}\right \} $
produce a matrix
$\left \{ da_{ij}\right \} $
produce a matrix
![]() $\mathcal {M}_{-CDA}(?)$
with
$\mathcal {M}_{-CDA}(?)$
with
![]() $\det \mathcal {M}_{-CDA}(?)\geq 0$
, then there is a tetrahedron
$\det \mathcal {M}_{-CDA}(?)\geq 0$
, then there is a tetrahedron
![]() $X\subset \mathbb {RH}^{3}$
with those dihedral angles.
$X\subset \mathbb {RH}^{3}$
with those dihedral angles.
Proof First, suppose we are given
![]() $X\subset \mathbb {RH}^{3}.$
We then have the triangle with vertices
$X\subset \mathbb {RH}^{3}.$
We then have the triangle with vertices
![]() $\widehat {X}.$
Let
$\widehat {X}.$
Let
![]() $\widehat {X}^{\#}$
be the polar dual of
$\widehat {X}^{\#}$
be the polar dual of
![]() $\widehat {X}$
, and let
$\widehat {X}$
, and let
![]() $X^{\#}$
be any tetrahedron in
$X^{\#}$
be any tetrahedron in
![]() $\mathbb {RH}^{3}$
with
$\mathbb {RH}^{3}$
with
![]() $\widehat {X^{\#}}=\widehat {X}^{\#}.$
Consider the matrix
$\widehat {X^{\#}}=\widehat {X}^{\#}.$
Consider the matrix
![]() $\mathcal {M} _{CVA}(X^{\#}).$
Its nondiagonal entries are of the form
$\mathcal {M} _{CVA}(X^{\#}).$
Its nondiagonal entries are of the form
![]() $\cos va_{i}^{\#}$
where
$\cos va_{i}^{\#}$
where
![]() $va_{i}^{\#}$
is a vertex angle of
$va_{i}^{\#}$
is a vertex angle of
![]() $X^{\#}.$
That vertex angle is also the length
$X^{\#}.$
That vertex angle is also the length
![]() $\ell _{i}^{\#}$
of the triangle
$\ell _{i}^{\#}$
of the triangle
![]() $\widehat {X^{\#}}.$
By Theorem 6.13, that length is given by
$\widehat {X^{\#}}.$
By Theorem 6.13, that length is given by
![]() $\ell _{i}^{\#}=\pi -a_{i}$
where
$\ell _{i}^{\#}=\pi -a_{i}$
where
![]() $a_{i}$
is an angle in the polar dual triangle (
$a_{i}$
is an angle in the polar dual triangle (
![]() $\widehat {X^{\#}})^{\#}=\widehat {X} ^{\#\#}=\widehat {X}.$
For any
$\widehat {X^{\#}})^{\#}=\widehat {X} ^{\#\#}=\widehat {X}.$
For any
![]() $\theta $
, we have
$\theta $
, we have
![]() $\cos \theta =-\cos (\pi -\theta ).$
Collecting these facts and comparing matrix entries, we see that
$\cos \theta =-\cos (\pi -\theta ).$
Collecting these facts and comparing matrix entries, we see that
![]() $\mathcal {M} _{CVA}(X^{\#})=\mathcal {M}_{-CDA}(X),$
Hence,
$\mathcal {M} _{CVA}(X^{\#})=\mathcal {M}_{-CDA}(X),$
Hence,
![]() $\det \mathcal {M}_{-CDA}(X)\geq 0$
is equivalent to
$\det \mathcal {M}_{-CDA}(X)\geq 0$
is equivalent to
![]() $\det \mathcal {M}_{CVA}(X^{\#})\geq 0.$
To see that that condition holds, recall that we are in real hyperbolic space and hence
$\det \mathcal {M}_{CVA}(X^{\#})\geq 0.$
To see that that condition holds, recall that we are in real hyperbolic space and hence
![]() $\mathcal {M}_{CVA}(X^{\#})=\mathcal {M}(X^{\#}).$
By Theorem 6.2, that last matrix is positive semidefinite and hence has a positive determinant.
$\mathcal {M}_{CVA}(X^{\#})=\mathcal {M}(X^{\#}).$
By Theorem 6.2, that last matrix is positive semidefinite and hence has a positive determinant.
The argument in the other direction is similar. Suppose we are given angles
![]() $da_{ij}$
which produce
$da_{ij}$
which produce
![]() $\mathcal {M}_{-CDA}(?)$
with
$\mathcal {M}_{-CDA}(?)$
with
![]() $\det \mathcal {M} _{-CDA}(?)\geq 0.$
Consider the supplementary angles
$\det \mathcal {M} _{-CDA}(?)\geq 0.$
Consider the supplementary angles
![]() $va_{ij}^{\#}=\pi -da_{ij}.$
By Theorem 5.1, the cosines of those angles can be used to form a matrix
$va_{ij}^{\#}=\pi -da_{ij}.$
By Theorem 5.1, the cosines of those angles can be used to form a matrix
![]() $\mathcal {M}(X)$
associated with a tetrahedron X. We now pass successively to
$\mathcal {M}(X)$
associated with a tetrahedron X. We now pass successively to
![]() $\widehat {X},$
the spherical triangle associated with
$\widehat {X},$
the spherical triangle associated with
![]() $X,$
then to
$X,$
then to
![]() $\widehat {X}^{\#},$
its polar dual, and finally
$\widehat {X}^{\#},$
its polar dual, and finally
![]() $Y,$
a tetrahedron whose associated spherical triangle
$Y,$
a tetrahedron whose associated spherical triangle
![]() $\widehat {Y}$
equals
$\widehat {Y}$
equals
![]() $\widehat {X}^{\#}.$
Tracking the changes, we see that we have passed to supplementary angles twice and hence the dihedral angles of Y are the
$\widehat {X}^{\#}.$
Tracking the changes, we see that we have passed to supplementary angles twice and hence the dihedral angles of Y are the
![]() $da_{ij}$
and Y is the desired tetrahedron.
$da_{ij}$
and Y is the desired tetrahedron.
7 Final comments
7.1 Cayley equations
If we replace the trigonometric variables in the expansion of
![]() $\det \mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})$
with algebraic variables, we obtain
$\det \mathcal {M}_{CVA}(\left \{ T_{i}\right \} _{i=2}^{4})$
with algebraic variables, we obtain
This polynomial was studied by Cayley in his classic study of cubic equations and sometimes carries his name [Reference HamptonH]. For us, the region in
![]() $\mathbb {R}^{3}$
where the variables have absolute value at most one and
$\mathbb {R}^{3}$
where the variables have absolute value at most one and
![]() $p(x,y,z)>0$
parameterizes nondegenerate tetrahedra in
$p(x,y,z)>0$
parameterizes nondegenerate tetrahedra in
![]() $\mathbb {RH}^{3}.$
The boundary surface
$\mathbb {RH}^{3}.$
The boundary surface
![]() $\Omega ,$
where
$\Omega ,$
where
![]() $p(x,y,z)=0,$
corresponds to degenerate tetrahedra. The smooth points of
$p(x,y,z)=0,$
corresponds to degenerate tetrahedra. The smooth points of
![]() $\Omega $
correspond to simple degenerations, degenerate tetrahedra that become nondegenerate when a single vertex is moved a small amount. The singular points of
$\Omega $
correspond to simple degenerations, degenerate tetrahedra that become nondegenerate when a single vertex is moved a small amount. The singular points of
![]() $\Omega $
correspond to more complicated, nongeneric, degeneracies. For instance, let T be a triangle
$\Omega $
correspond to more complicated, nongeneric, degeneracies. For instance, let T be a triangle
![]() $\left \{ w,y,z\right \} $
in the ball model of
$\left \{ w,y,z\right \} $
in the ball model of
![]() $\mathbb {RH}^{3}$
which is in the plane
$\mathbb {RH}^{3}$
which is in the plane
![]() $\mathbb {RH}^{2}$
specified by the vanishing of the third coordinate and which has the origin of that plane in its interior. Form tetrahedra
$\mathbb {RH}^{2}$
specified by the vanishing of the third coordinate and which has the origin of that plane in its interior. Form tetrahedra
![]() $X_{\varepsilon }$
by adjoining a fourth vertex, which will be the distinguished vertex
$X_{\varepsilon }$
by adjoining a fourth vertex, which will be the distinguished vertex
![]() $x_{1},$
with Euclidean coordinates
$x_{1},$
with Euclidean coordinates
![]() $\left ( 0,0,\varepsilon \right ) $
for a small positive
$\left ( 0,0,\varepsilon \right ) $
for a small positive
![]() $\varepsilon .$
The
$\varepsilon .$
The
![]() $X_{\varepsilon }$
are proper tetrahedra, but the limiting
$X_{\varepsilon }$
are proper tetrahedra, but the limiting
![]() $X_{0}$
whose vertices are the three starting points together with the origin as the distinguished vertex is degenerate. For
$X_{0}$
whose vertices are the three starting points together with the origin as the distinguished vertex is degenerate. For
![]() $X_{0}$
, the values of
$X_{0}$
, the values of
![]() $\operatorname *{kos}_{1}$
are the cosines of the angles formed by connecting the origin to the other vertices. We are in a plane, so those angles sum to 2
$\operatorname *{kos}_{1}$
are the cosines of the angles formed by connecting the origin to the other vertices. We are in a plane, so those angles sum to 2
![]() $\pi .$
Thus, the corresponding
$\pi .$
Thus, the corresponding
![]() $\left ( x,y,z\right ) $
values are
$\left ( x,y,z\right ) $
values are
![]() $\Lambda =\left ( \cos \alpha ,\cos \beta ,\cos \left ( 2\pi -\alpha -\beta \right ) \right ) $
for some angles
$\Lambda =\left ( \cos \alpha ,\cos \beta ,\cos \left ( 2\pi -\alpha -\beta \right ) \right ) $
for some angles
![]() $\alpha $
and
$\alpha $
and
![]() $\beta .$
Taking note of the fact that
$\beta .$
Taking note of the fact that
it is straightforward to check that
![]() $\Lambda $
is a point in the surface
$\Lambda $
is a point in the surface
![]() $\Omega .$
It is a smooth point, and the degeneracy of
$\Omega .$
It is a smooth point, and the degeneracy of
![]() $X_{0}$
can be removed by moving the vertex at the origin slightly to obtain an
$X_{0}$
can be removed by moving the vertex at the origin slightly to obtain an
![]() $X_{\varepsilon }.$
$X_{\varepsilon }.$
The singular points of
![]() $\Omega $
are the points (
$\Omega $
are the points (
![]() $\pm 1,\pm 1,\pm 1)$
with an even number of minus signs. The corresponding tetrahedra have four points on a single real geodesic. Those tetrahedra have nongeneric degeneracy, they remain degenerate if any one of the points is moved slightly.
$\pm 1,\pm 1,\pm 1)$
with an even number of minus signs. The corresponding tetrahedra have four points on a single real geodesic. Those tetrahedra have nongeneric degeneracy, they remain degenerate if any one of the points is moved slightly.
Some related discussion is in [Reference HamptonH].
7.2 Vertices at infinity
The study of tetrahedra in hyperbolic space, real or complex, is not restricted to classical bounded tetrahedra but also includes consideration of ideal tetrahedra, tetrahedra with one or more vertices in the ideal boundary (i.e., the “sphere at infinity,”
![]() $\partial \mathbb {B}_{n}$
). Although some of the previous discussion extends to those contexts, it is not clear if there are objects similar to the
$\partial \mathbb {B}_{n}$
). Although some of the previous discussion extends to those contexts, it is not clear if there are objects similar to the
![]() $DA(X)$
associated with these ideal tetrahedra. There is analysis of congruence of finite sets in the closure,
$DA(X)$
associated with these ideal tetrahedra. There is analysis of congruence of finite sets in the closure,
![]() $\overline {\mathbb {CH}^{n},}$
in several places including [Reference Cunha and GusevskiiCG, Reference GusevskiiG, Reference GoldmanGo, Reference Hakim and SandlerHS].
$\overline {\mathbb {CH}^{n},}$
in several places including [Reference Cunha and GusevskiiCG, Reference GusevskiiG, Reference GoldmanGo, Reference Hakim and SandlerHS].
7.3 The physics literature
The question of characterizing triples of triangles in
![]() $\mathbb {RH}^{3}$
which can be assembled as part of a tetrahedron is also studied in the physics literature, sometimes with the name “closure questions,” for instance, [Reference Bonzom, Dupuis, Girelli and LivineBDGL, Reference Christoph and LivineCL, Reference Haggard, Han and RielloHHR]. In contrast to the work here, those papers make substantial use of the descriptive and analytical properties of the automorphism group of hyperbolic space.
$\mathbb {RH}^{3}$
which can be assembled as part of a tetrahedron is also studied in the physics literature, sometimes with the name “closure questions,” for instance, [Reference Bonzom, Dupuis, Girelli and LivineBDGL, Reference Christoph and LivineCL, Reference Haggard, Han and RielloHHR]. In contrast to the work here, those papers make substantial use of the descriptive and analytical properties of the automorphism group of hyperbolic space.
7.4 Other Hilbert spaces and other geometries
We have worked with the Drury–Arveson kernel
![]() $k_{z}(w)=k(w,z)=\left ( 1-\left \langle \left \langle w,z\right \rangle \right \rangle \right )^{-1}.$
Similar questions can be considered for the Hilbert spaces generated by kernel functions
$k_{z}(w)=k(w,z)=\left ( 1-\left \langle \left \langle w,z\right \rangle \right \rangle \right )^{-1}.$
Similar questions can be considered for the Hilbert spaces generated by kernel functions
![]() $\left ( 1-\left \langle \left \langle w,z\right \rangle \right \rangle \right ) ^{-t}$
for
$\left ( 1-\left \langle \left \langle w,z\right \rangle \right \rangle \right ) ^{-t}$
for
![]() $t>0.$
Those functions are the reproducing kernels for various Besov–Sobolev spaces [Reference Arcozzi, Rochberg, Sawyer and WickARSW2] and also arise in other contexts [Reference MonodM]. In [Reference Ofek and SoferOS], it is shown that analogs of parts of Theorem 3.2 hold for those spaces if
$t>0.$
Those functions are the reproducing kernels for various Besov–Sobolev spaces [Reference Arcozzi, Rochberg, Sawyer and WickARSW2] and also arise in other contexts [Reference MonodM]. In [Reference Ofek and SoferOS], it is shown that analogs of parts of Theorem 3.2 hold for those spaces if
![]() $t\leq 2$
but not
$t\leq 2$
but not
![]() $t>2.$
$t>2.$
We have focused on the relationship between
![]() $DA(X)$
spaces and hyperbolic geometry. There are similar relationships between other classes of Hilbert spaces and other geometries, for instance, between the Segal–Bargmann–Fock spaces and the Hermitian geometry of
$DA(X)$
spaces and hyperbolic geometry. There are similar relationships between other classes of Hilbert spaces and other geometries, for instance, between the Segal–Bargmann–Fock spaces and the Hermitian geometry of
![]() $\mathbb {C}^{n}$
[Reference Arcozzi, Rochberg, Sawyer and WickARSW, Reference RochbergRo], and between the Hilbert spaces of spin coherent states, and the geometry of complex spheres and projective spaces [Reference Bengtsson and ŻyczkowskiBZ].
$\mathbb {C}^{n}$
[Reference Arcozzi, Rochberg, Sawyer and WickARSW, Reference RochbergRo], and between the Hilbert spaces of spin coherent states, and the geometry of complex spheres and projective spaces [Reference Bengtsson and ŻyczkowskiBZ].
More general relations between geometry and spaces such as
![]() $DA(X)$
for X in
$DA(X)$
for X in
![]() $\mathbb {RH}^{n}$
and
$\mathbb {RH}^{n}$
and
![]() $\mathbb {CH}^{n}$
are suggested by the work in [Reference MonodM].
$\mathbb {CH}^{n}$
are suggested by the work in [Reference MonodM].