We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
An infinite binary sequence is complex if the Kolmogorov complexity of its initial segments is bounded below by a computable function. We prove that a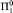 
class P contains a complex element if and only if it contains a wtt-cover for the Cantor set. That is, if and only if for every Y ⊆ ω there is an X in P such that X ≥wttY. We show that this is also equivalent to the 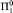class's being large in some sense. We give an example of how this result can be used in the study of scattered linear orders.
