Kristof has derived a theorem on the maximum and minimum of the trace of matrix products of the form \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$X_1 \hat \Gamma _1 X_2 \hat \Gamma _2\cdots X_n \hat \Gamma _n$$\end{document}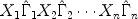 where the matrices \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \Gamma _i$$\end{document}
where the matrices \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \Gamma _i$$\end{document}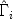 are diagonal and fixed and the Xi vary unrestrictedly and independently over the set of orthonormal matrices. The theorem is a useful tool in deriving maxima and minima of matrix trace functions subject to orthogonality constraints. The present paper contains a generalization of Kristof's theorem to the case where the Xi are merely required to be submatrices of orthonormal matrices and to have a specified maximum rank. The generalized theorem contains the Schwarz inequality as a special case. Various examples from the psychometric literature, illustrating the practical use of the generalized theorem, are discussed.
are diagonal and fixed and the Xi vary unrestrictedly and independently over the set of orthonormal matrices. The theorem is a useful tool in deriving maxima and minima of matrix trace functions subject to orthogonality constraints. The present paper contains a generalization of Kristof's theorem to the case where the Xi are merely required to be submatrices of orthonormal matrices and to have a specified maximum rank. The generalized theorem contains the Schwarz inequality as a special case. Various examples from the psychometric literature, illustrating the practical use of the generalized theorem, are discussed.