A Generalization of Kristof's Theorem on the Trace of Certain Matrix Products

Abstract

Kristof has derived a theorem on the maximum and minimum of the trace of matrix products of the form \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$X_1 \hat \Gamma _1 X_2 \hat \Gamma _2\cdots X_n \hat \Gamma _n$$\end{document} 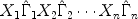where the matrices \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \Gamma _i$$\end{document} 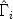are diagonal and fixed and the X_i vary unrestrictedly and independently over the set of orthonormal matrices. The theorem is a useful tool in deriving maxima and minima of matrix trace functions subject to orthogonality constraints. The present paper contains a generalization of Kristof's theorem to the case where the X_i are merely required to be submatrices of orthonormal matrices and to have a specified maximum rank. The generalized theorem contains the Schwarz inequality as a special case. Various examples from the psychometric literature, illustrating the practical use of the generalized theorem, are discussed.