We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a construction of the free dcpo-cone over any dcpo. There are two steps for getting this result. Firstly, we extend the notion of power domain to directed spaces which are equivalent to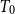 
$T_0$ monotone-determined spaces introduced by Erné, and we construct the probabilistic powerspace of the monotone determined space, which is defined as a free monotone determined cone. Secondly, we take D-completion of the free monotone determined cone over the dcpo with its Scott topology. In addition, we show that generally the valuation power domain of any dcpo is not the free dcpo-cone.
