A construction of free dcpo-cones

Abstract

We give a construction of the free dcpo-cone over any dcpo. There are two steps for getting this result. Firstly, we extend the notion of power domain to directed spaces which are equivalent to 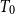$T_0$ monotone-determined spaces introduced by Erné, and we construct the probabilistic powerspace of the monotone determined space, which is defined as a free monotone determined cone. Secondly, we take D-completion of the free monotone determined cone over the dcpo with its Scott topology. In addition, we show that generally the valuation power domain of any dcpo is not the free dcpo-cone.

1. Introduction

Probabilistic power domain in domain theory plays an important role in modeling the semantics of nondeterministic functional programming languages with probabilistic choice. For example, the universal property of probabilistic power domain can help us define the sequential composition of two programs (Tix et al. 2009). Saheb-Djahromi (1980) considered probabilistic power domains over $\omega$ -algebraic dcpos, Escrig (1986) studied the case of SFP domains, and Jones (1990) extended the case to general dcpos. It is also shown by Jones and Gordon (1989) that the probabilistic power domain of a domain is still a domain and it has a kind of universal property. Kirch (1993) generalized Jones’ results to extended probabilistic power domain, and Tix (1995) proved that the extended probabilistic power domain of any domain is the free dcpo-cone. However, we show that the extended probabilistic power domain of a dcpo is generally not a free dcpo-cone in this paper. This leads to the question of: what the representation of free dcpo-cone over a non-continuous dcpo is. The aim of this paper is to deal with this problem. We believe that this construction can also be applied to study the algebra of valuation monad over the category of dcpos (Tix et al. 2009, p. 30).

The intuitive idea of our strategy consists of two steps: the first one is to construct some kind of variation of free cone and the next step is to consider an appropriate completion of this free object. To achieve our goal we will need two tools – directed spaces and D-completions. Directed spaces were introduced independently by Yu and Kou (2015), which are equivalent to the $T_0$ monotone-determined spaces defined by Erné (2009). They can be regarded as a topological extended model of domain theory. A monotone determined space is a $T_0$ space whose topology can be determined by its convergent directed subsets. For instance, every dcpo endowed with the Scott topology is a monotone determined space. The category of monotone determined spaces with continuous maps is a Cartesian closed category, and many properties of dcpos can be extended to monotone determined spaces (Yu and Kou 2015). A natural question arises: what is a monotone determined version of extended probabilistic powerspace over a monotone determined space? To answer this question, we have to do two things. The first one is to define a monotone determined cone by using Keimel’s topological cone (Keimel 2008), just like the d-cone (Gierz et al. 2003). The second one is to construct a free object over any monotone determined space. We give a concrete construction of extended probabilistic powerspace over any monotone determined space. After that we get a representation of free dcpo-cone over any dcpo L by taking the D-completion of the monotone determined probabilistic powerspace over the Scott space $\Sigma L$ .

The paper is organized as follows. In Section 2, we introduce the concept of directed spaces and their properties. In the next section, we define the notion of a monotone determined cone and then give its concrete representation by constructing an appropriate topology on the set of simple valuations. In Section 4, we recall some useful results of D-completion and Scott completion. In addition, we exhibit the free dcpo-cone over any dcpo, which provides an answer to the problem of characterizing the probabilistic power domains of general dcpos. In the final section, we show that the valuation power domain over a dcpo D is not always the free dcpo-cone on D by considering an example by Goubault and Jia (2021).

2. Preliminaries

First, we introduce some basic concepts. For basic knowledge and notations in domain theory, topology, and category theory, we refer to Abramsky and Jung (1994), Gierz et al. (2003),MacLane (1971).

Let P be a partially ordered set (poset for short). Given any subset $A\subseteq P$ , denote $\mathord{\downarrow} A=\{x\in P: \exists a\in A,\ \ x\leq a\}$ , $\mathord{\uparrow} A=\{x\in P: \exists a\in A,\ a\leq x\}$ . We say that A is a lower set (upper set) if $A=\mathord{\downarrow} A$ ( $A=\mathord{\uparrow} A$ ). A nonempty set $D\subseteq P$ is called a directed set if each finite nonempty subset of D has an upper bound in D. A poset P is called a directed complete poset, abbreviated as a dcpo, if each directed subset D of P has a supremum (denoted by $\bigvee D$ ). A subset U of a poset P is called a Scott open subset if U is an upper set and for each directed subset $D\subseteq P$ such that $\bigvee D$ exists and belongs to U, $U\cap D\not=\emptyset$ . The set of all Scott open subsets of a poset P form a topology on P, which is called the Scott topology and denoted by $\sigma(P)$ . A topological space is called a Scott space if it is a dcpo endowed with the Scott topology. We denote by $\Sigma P = (P,\sigma(P))$ . Suppose that P and E are two posets, a map $f:P\longrightarrow E$ is called Scott continuous if it is continuous with respect to $\sigma(P)$ and $\sigma(E)$ . A poset L is called a complete lattice if any subset has a supremum in L. We say $x\lll y$ in L, if for any set A with $y\leq\bigvee A$ , there exists some $a\in A$ such that $x\leq a$ . A complete lattice L is prime continuous if for any $x\in L$ , $x=\bigvee\{y\in L:y\lll x\}$ .

All topological spaces in this paper are supposed to be $T_0$ spaces. A net in a topological space X is a map $\xi: J\longrightarrow X$ , where J is a directed set. Usually, we denote a net by $(x_j)_{j\in J}$ or $(x_j)$ . We say that $(x_j)$ converges to x, denoted by $(x_j)\rightarrow x$ or $x\equiv \lim x_j$ , if $(x_j)$ is eventually in every open neighborhood of x, that is, for every open neighborhood U of x, there exists $j_0\in J$ such that for every $j\in J$ , $j\geq j_0\Rightarrow x_j\in U$ .

Let X be a $T_{0}$ topological space with its topology denoted by $\mathcal{O}(X)$ . Then, the specialization order on X is defined as follows:

\[\forall x, y \in X,\ x\sqsubseteq y \Leftrightarrow x\in \overline{\{y\}}\]

where $\overline{\{y\}}$ denotes the closure of $\{y\}$ . From now on, the order of a $T_{0}$ topological space always indicates the specialization order “ $\sqsubseteq$ ”.

Supposing that X is a $T_{0}$ space, then every directed set $D\subseteq X$ can be regarded as a net $(d)_{d \in D}$ in X. We use $D\rightarrow x$ or $x\equiv \lim D$ to represent that D converges to x. Define

\[D(X)=\{(D, x):x\in X,\ D \text{ is a directed subset of } X \text{ and } D\rightarrow x \}.\]

It is easy to verify that, for every $x, y\in X$ , $x\sqsubseteq y\Longleftrightarrow \{y\}\rightarrow x$ . Therefore, if $x\sqsubseteq y$ then $(\{y\},\ x)\in D(X)$ . Next, we introduce the concept of monotone determined spaces.

Definition 1. (Yu and Kou 2015) Let X be a $T_{0}$ space.

1. (1) A subset U of X is called a directed open set if $\forall (D,\ x)\in D(X),\ x\in U \Rightarrow D\cap U\neq \emptyset$ . Denote the set of all directed open subsets of X by d(X).

2. (2) X is called a monotone determined space if each directed open subset of X is an open subset, that is, $d(X)= \mathcal{O}(X)$ .

Dcpos endowed with the Scott topology are monotone determined spaces and many properties of dcpos can be extended to monotone determined spaces. The topology on a monotone determined space need not be Scott topology; for example, every poset with the Alexanderoff topology is a monotone determined space. The natural numbers with co-finite topology are not a monotone determined space. For more details, we refer to Yu and Kou (2015).

Monotone determined spaces with continuous maps as morphisms form a Cartesian closed category, denoted by Dtop. In the following, we introduce the representation and some basic properties of categorical product of monotone determined spaces in $\bf Dtop$ .

Suppose that $X,\ Y$ are two monotone determined spaces. Let $X\times Y$ be the Cartesian product of X and Y, then we have a natural partial order on it: $\forall (x_{1}, y_{1}), (x_{2}, y_{2})\in X\times Y$ ,

\[(x_{1}, y_{1})\leq(x_{2}, y_{2})\iff x_{1}\sqsubseteq x_{2}, y_{1}\sqsubseteq y_{2}.\]

which is called the pointwise order on $X\times Y$ . Now, we define a topological space $X\otimes Y$ as follows:

1. (1) The underlying set of $X\otimes Y$ is $X\times Y$ ;

2. (2) The topology on $X\otimes Y$ is generated as follows: for each given $\leq$ - directed set $D\subseteq X\times Y$ and $(x, y)\in X\times Y$ , define

   \[D\rightarrow_d(x, y)\in X\otimes Y\iff\pi_{1}D\rightarrow x\in X,\ \pi_{2}D\rightarrow y\in Y. \]
   A subset $U\subseteq X\otimes Y$ is open iff for every $D\rightarrow_d (x, y)$ as defined above, $(x, y)\in U\Longrightarrow U\cap D\neq\emptyset$ .

Theorem 2. (Yu and Kou 2015) Let X and Y be two monotone determined spaces.

1. (1) The topological space $X\otimes Y$ defined as above is a monotone determined space, and the specialization order on $X\otimes Y$ is equal to the pointwise order on $X\times Y$ .

2. (2) Let Z be a monotone determined space. Then $f:X\otimes Y\longrightarrow Z$ is continuous if and only if it is continuous in each argument separately.

Definition 3. Let $X,\ Y$ be two $T_{0}$ spaces. A map $f:X\longrightarrow Y$ is called directed continuous if it is monotone and preserves all limits of directed subsets of X, that is, $(D, x)\in D(X)\Rightarrow(f(D),f(x))\in D(Y)$ .

Proposition 4. (Yu and Kou 2015) Let $X,\ Y$ be two $T_{0}$ spaces, and $f:X\longrightarrow Y$ be a map from X to Y.

1. (1) f is directed continuous if and only if $\forall U\in d(Y),\ f^{-1}(U)\in d(X)$ .

2. (2) If $X,\ Y$ are monotone determined spaces, then f is continuous if and only if it is directed continuous.

Let P be a dcpo, and $x,\ y\in P$ . We say that x is way-below y, if for each given directed set $D\subseteq P$ , $y\leq\bigvee D$ implies that there exists some $d\in D$ such that $x\leq d$ . We write

Definition 5. A dcpo P is called a domain if for each $x\in P$ , x is directed and

A $T_0$ topological space X is a c-space if for each $x\in X$ and each open neighborhood U of x, there exists some $y\in U$ such that $x\in ({\uparrow y})^\circ \subseteq U$ . The c-spaces are classical spaces investigated by many scholars. Continuous domains endowed with the Scott topology are c-spaces, and c-spaces are monotone determined spaces (Erné 2009).

The following result gives a characterization of c-space.

Proposition 6. (Goubault-Larrecq 2013, Lemmas 8.3.41, 8.3.42) A $T_0$ space is a c-space iff the lattice $\mathcal{O}(X)$ with the inclusion order is prime continuous.

3. The Monotone Determined Probabilistic Powerspaces

As mentioned above, monotone determined spaces form a very natural topological extended model of dcpos in Domain theory. Like the work done by Battenfeld and Schöder (1994), extending the power domain to the category of monotone determined spaces is useful. In this section, we will construct the monotone determined probabilistic powerspace of an arbitrary monotone determined space, which is a free algebra generated by the addition and scalar multiplication over the monotone determined space.

Definition 7. (Heckmann 1996) Let X be a topological space. A map $\mu:\mathcal{O}(X)\longrightarrow[0, +\infty]$ is called a continuous valuation if the following hold:

1. (1) strictness: $\mu(\emptyset)=0$ ;

2. (2) monotonicity: $\forall V\subseteq U\in\mathcal{O}(X)$ $\implies$ $\mu(V)\leq\mu(U)$ ;

3. (3) modular law: $\mu(U)+\mu(V)=\mu(U\cup V)+\mu(U\cap V), \forall U,V\in\mathcal{O}(X)$ ;

4. (4) continuity: for each directed subset $\mathcal{D}$ , also called a directed family of $\mathcal{O}(X)$ , $\mu(\sup\mathcal{D})=\sup\{\mu(U):U\in\mathcal{D}\}$ .

$\mathcal{V}(X)$ stands for the set of continuous valuations over X.

Definition 8. (Heckmann 1996) A continuous valuation $\mu$ is called a point-continuous valuation if for any non-negative real number r and any open set U of X with $\mu(U)>r$ , there is a finite set $F\subseteq U$ such that $\mu(V)>r$ for any open set $V\supseteq F$ . Let $\mathcal{V}_{p}(X)$ denote the set of all point-continuous valuations over X.

Definition 9. (Gierz et al. 2003, Definition IV-9.9) Let X be a topological space. For each $x\in X$ , we define the point valuation $\eta_x:\mathcal{O}(X)\longrightarrow [0,+\infty]$ as follows: $\eta_x(U)=1$ if $x\in U$ , and $\eta_x(U)=0$ if $x\notin U$ . A finite linear sum $\xi=\sum_{b\in B}r_b\eta_b$ with $0< r_b < +\infty$ , defined by $\xi(U)=\sum_{b\in U}r_b$ , is called a simple valuation. The set $B=\text{supp}\xi$ is called the support of $\xi$ . We denote the set of all simple valuations by $\mathcal{V}_{f}(X)$ .

The following lemma shows that every simple valuation has a unique representation as a linear combination of point valuations.

Lemma 10. (Gierz et al. 2003, Lemma IV-9.22) Let $\zeta=\sum_{b\in B}r_b\eta_b$ and $\sum_{c\in C}s_c\eta_c=\xi$ be two simple valuations on $\mathcal{O}(X)$ , where X is a $T_0$ space. If $\xi$ and $\zeta$ are distinct as linear combinations, then they are distinct as valuations.

Topological cones were defined by Keimel (2008). In the following, we replace the $T_0$ space by monotone determined space to give the definition of monotone determined cone.

Definition 11. A monotone determined cone is a monotone determined space X equipped with a distinguished element $0\in X$ , an addition $+:X\otimes X\rightarrow X$ , and a scalar multiplication $\cdot:\mathbb{R}^+\otimes X\rightarrow X$ ( $\mathbb{R}^+$ endowed with the Scott topology in its usual partial order) such that both operations are continuous and the following are satisfied.

1. (1) $x+y=y+x$ , $\forall x,\ y\in X$ ,

2. (2) $(x+y)+z=x+(y+z)$ , $\forall x,\ y,\ z\in X$ ,

3. (3) $0+x=x,\ \forall x\in X$ ,

4. (4) $(kl)\cdot x=k\cdot(l\cdot x),\ \forall k,\ l\in\mathbb{R}^+,\forall x\in X$ ,

5. (5) $(k+l)\cdot x=(k\cdot x)+(l\cdot x)$ , $\forall k,\ l\in\mathbb{R}^+,\ \forall x\in X$ ,

6. (6) $k\cdot(x+y)=(k\cdot x)+(k\cdot y),\ \forall k\in\mathbb{R^+},\ \forall x,\ y\in X$ ,

7. (7) $1\cdot x=x,\ \forall x\in X$ ,

8. (8) $k\cdot 0=0$ , $\forall k\in\mathbb{R}^+$ .

Definition 12. Let $(X, +, \cdot)$ , $(Y, \uplus, \ast)$ be two monotone determined cones. A map $f:(X, +, \cdot)\rightarrow (Y, \uplus, \ast)$ is called a monotone determined cone homomorphism between X and Y, if f is continuous and $f(x+ y)=f(x)\uplus f(y)$ and $f(a\cdot x)=a\ast f(x)$ hold for all $x, y\in X$ , and $a\in\mathbb{R}^+=[0,+\infty)$ .

Denote the category of all monotone determined cones and monotone determined cone homomorphisms by Dscone. Then Dscone is a subcategory of Dtop. Now, we define the notion of monotone determined probabilistic powerspaces.

Definition 13. Let X be a monotone determined space. A monotone determined cone $(Z,+,\cdot)$ is called the monotone determined probabilistic powerspace of X if there is a continuous map $i:X\longrightarrow Z$ that satisfies the following property: for arbitrary monotone determined cone $(Y,\ \uplus,\ \ast)$ and continuous map $f:X\longrightarrow Y$ , there exists a unique monotone determined cone homomorphism $\bar{f}:(Z,\ +,\ \cdot)\rightarrow (Y,\ \uplus,\ \ast)$ such that $f=\bar{f}\circ i$ .

By the definition above, if monotone determined cones $(Z_1, +, \cdot)$ and $(Z_2, \uplus, \ast)$ are both the monotone determined probabilistic powerspaces of X, then there exists a topological homomorphism which is also a monotone determined cone homomorphism $g:Z_1\rightarrow Z_2$ . Therefore, up to isomorphism, the monotone determined probabilistic powerspace of a monotone determined space is unique. Hence, we denote the monotone determined probabilistic powerspace of each monotone determined space X by $P_D(X)$ .

Now, we show the existence of monotone determined probabilistic powerspaces by giving the concrete construction of the monotone determined probabilistic powerspace of any monotone determined space X.

For any monotone determined space X, there is a natural pointwise order $\leq$ on $\mathcal{V}_f(X)$ :

\[\xi\leq\eta\iff \xi(U)\leq\eta(U),\ \forall U\in\mathcal{O}(X).\]

In the following, we will introduce a new convergence on the set of simple valuations.

Definition 14. Let $\mathcal{D}=\{\xi_i\}_{i\in I} $ be a directed subset of $\mathcal{V}_f(X)$ in the pointwise order and $\xi\in \mathcal{V}_f(X)$ with nonempty support. We write $\mathcal{D}\Rightarrow_P \xi$ if there is a representation of $\xi$ as $\sum_{i=1}^n r_{b_i}\eta_{b_i}$ ( $r_{b_i}>0$ for each i, $b_i$ may be equal to $b_j$ for $i\neq j$ ), and there exist directed subsets $D_1,\cdots,D_n\subseteq X$ satisfying $\forall i\in\{1,\cdots,n\}: D_i\rightarrow b_i$ in X, such that for any $(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$ and $r_{b_i}'<r_{b_i}$ (for $i=1,\dots,n$ ), there exists some $\xi'\in\mathcal{D}$ such that $\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$ . If the support of $\xi$ is $\emptyset$ , then $\xi=0$ . We define that any directed subset of $\mathcal{V}_f(X)$ always converges to 0.

A subset $\mathcal{U}\subseteq \mathcal{V}_f(X)$ is called a $\Rightarrow_P$ convergence open subset of $\mathcal{V}_f(X)$ if and only if for each directed subset $\mathcal{D}$ of $\mathcal{V}_f(X)$ and $\xi\in \mathcal{V}_f(X)$ , $\mathcal{D}\Rightarrow_{P}\xi\in \mathcal{U}$ implies $\mathcal{D}\cap \mathcal{U}\neq \emptyset$ . Denote the set of all $\Rightarrow_P$ convergence open subsets of $\mathcal{V}_f(X)$ by $O_{\Rightarrow_{P}}(\mathcal{V}_f(X))$ .

Proposition 15. Let X be a monotone determined space. Then, the following statements hold.

1. (1) $(\mathcal{V}_f(X),\ O_{\Rightarrow_P}(\mathcal{V}_f(X)))$ is a topological space, henceforth, denoted as CX.

2. (2) The specialization order $\sqsubseteq $ on CX is equal to the pointwise order.

3. (3) CX is a monotone determined space, that is, $O_{\Rightarrow_P}(\mathcal{V}_f(X))=d(CX)$ .

Proof. (1) Obviously, $\emptyset,\ CX\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$ . Suppose that $\mathcal{U}\in O_{\Rightarrow_U}(\mathcal{V}_f(X)$ ), $\xi\leq\eta$ , $\xi\in\mathcal{U}$ , and $\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$ . Then, it is evident that $\{\eta\}\Rightarrow_{P}\xi$ , since we only need to take $D_{i}=\{b_{i}\}$ for $\ i=1,\dots,n$ . Then, $\{\eta\}\cap \mathcal{U} \neq \emptyset$ , this means $\eta\in \mathcal{U}$ , and thus $\mathcal{U}$ is an upper set with respect to the pointwise order $\leq$ .

Let $\mathcal{U}_{1},\mathcal{U}_{2}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$ , and $\mathcal D$ be a directed subset of $\mathcal{V}_f(X)$ with $\mathcal{D}\Rightarrow_{P} \xi\in \mathcal{U}_{1}\cap\mathcal{U}_{2}$ . Then, there exists some $\xi_{1}\in \mathcal{D}\cap \mathcal{U}_{1}$ and $ \xi_{2}\in \mathcal{D}\cap \mathcal{U}_{2}$ . Since $\mathcal{D}$ is directed, there exists some $\xi_{3}\in \mathcal{D}$ such that $\xi_{3}\geq\xi_{1},\ \xi_{2}$ . Then, $\xi_{3}\in \mathcal{D}\cap \mathcal{U}_{1}\cap\mathcal{U}_{2}$ , and then $\mathcal{U}_{1}\cap\mathcal{U}_{2} \in O_{\Rightarrow_P}(\mathcal{V}_f(X))$ . In the same way, we can show that $O_{\Rightarrow_U}(\mathcal{V}_f(X))$ is closed under arbitrary unions. Hence, $O_{\Rightarrow_U}(\mathcal{V}_f(X))$ is a topology.

(2) By the proof of (1), each $\Rightarrow_P$ convergence open set is an upper set with respect to the pointwise order. We only need to prove that $\downarrow_{\leq}\eta$ is a closed set in CX. Equivalently, we show that $CX\setminus\downarrow_{\leq}\eta$ is a $\Rightarrow_{P}$ convergence open set.

Set $\mathcal{U}=CX\setminus\downarrow_{\leq}\eta$ and $\mathcal{D}\Rightarrow_{P}\xi\in\mathcal{U}$ . To obtain a contradiction, suppose $\mathcal{U}\cap\mathcal{D}=\emptyset$ , that is, $\forall\xi'\in\mathcal{D},\xi'\leq\eta$ . By the definition of $\mathcal{D}\Rightarrow_{P}\xi$ , there is a representation $\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$ , and we have directed sets $D_1,\dots,D_n\subseteq X$ with $D_i\rightarrow b_i,i=1,\dots,n$ , and for any $ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$ and any $r_{b_{i}}'<r_{b_{i}} (1\leq i\leq n)$ , there exists some $\xi'\in\mathcal{D}$ such that $\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$ . Now, we claim that $\xi\leq\eta$ , which contradicts $\xi\in\mathcal{U}$ . By the definition of pointwise order $\leq$ , for any $ U\in\mathcal{O}(X)$ , we may assume that $b_1,\dots,b_k\in U,0\leq k\leq n$ . Since $D_i\rightarrow b_i,i=1,\dots,k$ , there exists $(d_1,\dots,d_k)\in\prod_{i=1}^{k}D_i$ such that $d_i\in U$ . For each $r_{b_{i}}'<r_{b_{i}},i=1,\dots,k$ , there exists $\xi'\in\mathcal{D}$ such that $\sum_{i=1}^{k} r_{b_i}'\eta_{d_i}\leq\xi'$ . Note that $k\leq n$ , then,

\[\left(\sum_{i=1}^{k} r_{b_i}'\eta_{b_i}\right)(U)=\sum_{i=1}^{k} r_{b_i}'\leq\xi'(U)\leq\eta(U).\]

But the supremum of the left hand side is $\sum_{i=1}^{k} r_{b_i}=(\sum_{i=1}^{k}r_{b_{i}}\eta_{b_i})(U)=\xi(U)$ .

(3) For an arbitrary topological space X, $\mathcal{O}(X)\subseteq d(X)$ holds. Thus, $O_{\Rightarrow_P}(\mathcal{V}_f(X))\subseteq d(CX)$ . On the other hand, according to the definition of $\Rightarrow_P$ convergence topology, if $\mathcal D\subseteq CX$ is directed and $ \mathcal{D}\Rightarrow_{P}\xi$ , then $\mathcal{D}$ converges to $\xi$ with respect to $O_{\Rightarrow_P}(\mathcal{V}_f(X))$ . By the definition of directed open set, $\mathcal{D}\Rightarrow_{P}\xi \in\mathcal{U}\in d(CX)$ will imply $\mathcal{U}\cap \mathcal{D}\neq \emptyset$ . Then, $\mathcal{U}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$ , it follows that $O_{\Rightarrow_P}(\mathcal{V}_f(X))= d(CX)$ , that is, CX is a monotone determined space.

Proposition 16. Suppose that $X,\ Y$ are two monotone determined spaces. Then, a map $f:CX\rightarrow Y$ is continuous if and only if for each directed subset ${\mathcal D}\subseteq CX$ and $\xi\in CX$ , ${\mathcal D}\Rightarrow_P\xi$ implies $f(\mathcal{D})\rightarrow f(\xi)$ .

Proof. Since $\Rightarrow_P$ convergence will lead to topological convergence in CX, the necessity is obvious. We need only to prove the sufficiency. First, we check that f is monotone. If $\xi,\ \eta\in CX$ and $\xi\leq\eta$ , then $\{\eta\}\Rightarrow_P\xi$ , by the hypothesis, $\{f(\eta)\}\rightarrow f(\xi)$ , thus $f(\xi)\sqsubseteq f(\eta)$ . Suppose that U is an open subset of Y and the directed set ${\mathcal D}\Rightarrow_P\xi\in f^{-1}(U)$ , then $f(\mathcal{D})$ is a directed set of Y and $f(\mathcal{D})\rightarrow f(\xi)\in U$ , thus $\exists\ \xi'\in {\mathcal D}$ such that $f(\xi')\in U$ . That is, $\xi'\in {\mathcal D}\cap f^{-1}(U)$ . According to the definition of $\Rightarrow_P$ convergence open set, $f^{-1}(U)\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$ , which means that f is continuous.

The addition operation on CX is defined as follows:

\[\forall \xi, \eta\in CX,\ (\xi +\eta)(U)=\xi(U)+\eta(U),\ \forall U\in\mathcal{O}(X).\]

And the scalar multiplication operation on CX is defined as follows:

\[\forall a\in\mathbb{R}^{+},\ \forall \xi\in CX,\ (a\cdot\xi)(U)=a\xi(U).\]

We now check that the two operations are both continuous, and thus, $(CX, +, \cdot)$ is a monotone determined cone.

Theorem 17. Let X be a monotone determined space. Then, $(CX, +, \cdot)$ is a monotone determined cone.

Proof. By Proposition 15, CX is a monotone determined space, and by the definition of $+$ and $\cdot$ , the two operations are monotone. According to Theorem 2 and Proposition 16, to prove the continuity of $+$ , we only need to check that for arbitrary fixed $\eta=\sum_{j=1}^{m}s_{c_j}\eta_{c_j}\in CX $ ( $c_{j_1}\neq c_{j_2}$ for different $j_1$ and $j_2$ ) and a directed set $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$ with $\mathcal{D}\Rightarrow_{P}\xi$ , we have $\mathcal{D}+\eta =\{\xi_i +\eta\}_{i\in I}\Rightarrow_{P}\xi +\eta$ . Assume that $\xi$ has a representation $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$ and there exist $D_1,\cdots,D_n$ – with $D_i\rightarrow b_i$ for $1\leq i\leq n$ – as in the definition of $\mathcal{D}\Rightarrow_{P}\xi$ .

For an arbitrary $(d_1,\dots,d_n,c_1,\dots,c_m)\in\prod_{i=1}^{n}D_i\times\prod_{j=1}^{m}\{c_j\}$ , and $\forall r_{b_i}'<r_{b_i},\ s_{c_j}'<s_{c_j},\ i=1,\dots,n,j=1,\dots,m$ , by the definition of $\mathcal{D}\Rightarrow_{P}\xi$ , there exists some $\xi'\in\mathcal{D}$ such that $\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}\leq\xi'$ . Since $+$ is monotone,

\[\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq\xi'+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq \xi'+\eta.\]

Now, we prove continuity of scalar product. For an arbitrary fixed $a\in\mathbb{R}^+$ and a directed set $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$ with $\mathcal{D}\Rightarrow_{P}\xi$ , we claim that $a\cdot\mathcal{D}=\{a\cdot\xi_i\}_{i\in I}\Rightarrow_{P}(a\cdot\xi)$ . By the hypothesis of $\mathcal{D}\Rightarrow_{P}\xi$ there is a representation of $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$ and we have $D_1,\cdots,D_n$ – with $D_i\rightarrow b_i$ for $1\leq i\leq n$ , for $\forall\ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i,\ \forall\ r_{b_i}'<r_{b_i},i=1,\dots,n$ , there exists $\xi'\in\mathcal{D}$ , such that $\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$ . Hence, we have $\sum_{i=1}^{n}a\cdot r_{b_i}'\eta_{d_i}\leq a\cdot\xi'$ .

For arbitrary $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$ and a directed set $D\subseteq\mathbb{R}^+$ with $D\rightarrow a$ . We claim that $D\cdot\xi=\{d\cdot\xi\}_{d\in D}\Rightarrow_{P}(a\cdot\xi)$ . Let $D_i=\{b_i\},i=1,\dots,n$ , $\forall\ (b_1,\dots,b_n)\in\prod_{i=1}^{n}D_i$ and $\forall\ r_{b_i}'<ar_{b_i},i=1,\dots,n$ , we only need to find $d\in D$ with $r_{b_i}'\leq dr_{b_i},i=1,\dots,n.$ This is possible, because for each $i=1,\dots,n$ , $\dfrac{r_{b_i}'}{r_{b_i}}<a$ and $D\rightarrow a$ .

In conclusion, $(CX, +, \cdot)$ is a monotone determined cone.

We now show that $(CX, +, \cdot)$ is the free monotone determined cone over X. It is the main result of this section. We begin with one useful lemma.

Proposition 18. (Gierz et al. 2003, Proposition IV-9.18) (Splitting Lemma) For two simple valuations in $\mathcal{V}_f(X)$ , where X is a $T_0$ space, we have $\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$ if and only if there exist $\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$ such that for each $b\in B,\ c\in C$ ,

\[\sum\limits_{c\in C}t_{b,c}=r_b,\ \sum_{b\in B}t_{b,c}\leq s_c\]

and $t_{b,c}\neq 0$ implies $b\leq c$ .

Theorem 19. Let X be a monotone determined space. Then $(CX, +, \cdot)$ is the monotone determined probabilistic powerspace over X, that is, endowed with topology $O_{\Rightarrow_P}(\mathcal{V}_f(X))$ , $(CX, +, \cdot)\cong P_D(X)$ .

Proof. Define the map $i:X\rightarrow CX$ as follows: $\forall x\in X$ , $i(x)=\eta_x$ . By Lemma 10, i is injective. We now prove the continuity of i. It is evident that if $x\leq y\in X$ then $\forall U\in\mathcal{O}(X),\ x\in U \Longrightarrow y\in U$ , that is, $\eta_x\leq\eta_y$ . Suppose that D is a directed subset of X with $D \rightarrow x\in X$ . Let $\mathcal{D}=\{\eta_d:d\in D\}$ , then $i(D)=\mathcal{D}$ is a directed set in CX and ${\mathcal D}\Rightarrow_{P}\eta_x$ . Because, by hypothesis, $D\rightarrow x$ , and $\forall d\in D,\ \forall k<1\ :\ k\eta_d\leq\eta_d$ .

Let $(Y, \uplus, \ast)$ be a monotone determined cone and $f:X\rightarrow Y$ be a continuous map. Define $\bar{f}:CX\rightarrow Y$ as follows: $\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX (\text{supp}(\xi)=\{b_1,\cdots,b_n\})$ ,

\[\bar{f}(\xi)=\biguplus\limits_{i=1}^{n}r_{b_i}\ast f(b_i).\]

By Lemma 10, $\bar{f}$ is well-defined.

1. (1) $f=\bar{f}\circ i$ .

For arbitrary $x\in X$ , $(\bar{f}\circ i)(x)=\bar{f}(i(x))=\bar{f}(\eta_x)=f(x)$ .

1. (2) $\bar{f}$ is a monotone determined cone homomorphism, that is, $\bar{f}$ is continuous and for arbitrary $\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$ , $\bar{f}(\sum_{i=1}^{n}r_{b_i}\eta_{b_i})=\biguplus_{i=1}^{n}r_{b_i}\ast\bar{f}(\eta_{b_i})$ . This equation is evident since $\bar{f}(\eta_{b_i})=f(b_i),\ i=1,\dots,n.$ So, we only need to prove that $\bar{f}$ is continuous.

First, $\bar{f}$ is monotone. Let $\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$ . By Proposition 18, there exist $\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$ such that for each $b\in B,\ c\in C$ ,

\[\sum\limits_{c\in C}t_{b,c}=r_b,\ \sum_{b\in B}t_{b,c}\leq s_c\]

and $t_{b,c}\neq 0$ implies $b\leq c$ . From the definition of $\bar{f,}$ we have

\[\bar{f}(\zeta)=\biguplus_{b\in B}r_b\ast f(b)=\biguplus\limits_{b\in B}\biguplus\limits_{c\in C}t_{b,c}\ast f(b)\leq\biguplus\limits_{c\in C}\biguplus\limits_{b\in B}t_{b,c}\ast f(c)\leq\biguplus\limits_{c\in C}s_{c}\ast f(c)=\bar{f}(\xi).\]

By Proposition 16, to show the continuity of $\overline{f}$ , we need only to prove that $\bar{f}$ preserves $\Rightarrow_{P}$ convergence class. Suppose that we have a directed set $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$ and $\xi\in CX$ with $\mathcal{D}\Rightarrow_{P}\xi$ , then, we need to show that $\bar{f}(\mathcal{D})\rightarrow\bar{f}(\xi)$ in Y. There is a representation $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$ and let $D_1,\cdots,D_n$ with $D_i\rightarrow b_i (1\leq i\leq n)$ be as in the definition of $\mathcal{D}\Rightarrow_{P}\xi$ . From the continuity of $f,\ \uplus$ and $\ast$ , we have

\[\mathcal{E}=(r_{b_1}'\ast f(D_1))\uplus\dots\uplus (r_{b_n}'\ast f(D_n))\rightarrow\biguplus\limits_{i=1}^nr_{b_i}\ast f(b_i)=\bar{f}(\xi).\]

Notice that $\mathcal{E}=\{(r_{b_1}'\ast f(d_1))\uplus\dots\uplus (r_{b_n}'\ast f(d_n)):(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i, r_{b_i}'<r_{b_i},i=1,\cdots,n\}$ is a directed set in Y. For an arbitrary open neighborhood U of $\bar{f}(\xi)$ , there exists some $(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$ and $r_{b_i}'<r_{b_i},i=1,\cdots,n$ such that $\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\in U$ . For the given $d_1,\dots,d_n$ and $r_{b_i}'<r_{b_i},i=1,\dots,n$ , again by the definition of $\mathcal{D}\Rightarrow_{P}\xi$ , there exists some $\xi'\in\mathcal{D}$ such that $\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$ . Then $\bar{f}(\sum_{i=1}^{n}r_{b_i}'\eta_{d_i})=\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\leq\bar{f}(\xi')$ . Since U is an upper set, then $\bar{f}(\xi')$ is included in U. Hence, $\bar{f}$ is continuous.

1. (3) The homomorphism $\bar{f}$ is unique.

Suppose we have a monotone determined cone homomorphism $g:(CX, +, \cdot)\rightarrow (Y, \uplus, \ast)$ such that $f=g\circ i$ , then $g(\eta_x)=f(x)=\bar{f}(\eta_x)$ . For each $ \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$ ,

\begin{eqnarray*} g(\xi)&=& g(r_{b_1}\eta_{b_1}+r_{b_2}\eta_{b_2}\cdots+r_{b_n}\eta_{b_n})\\ &=&g(r_{b_1}\eta_{b_1})\uplus g(r_{b_2}\eta_{b_2})\uplus \cdots \uplus g(r_{b_n}\eta_{b_n})\\ &=&r_{b_1}\ast g(\eta_{b_1})\uplus r_{b_2}\ast g(\eta_{b_2})\uplus \cdots\uplus r_{b_n}\ast g( \eta_{b_n})\\ &=&r_{b_1}\ast f({b_1})\uplus r_{b_2}\ast f({b_2})\uplus \cdots\uplus r_{b_n}\ast f({b_n})\\ &=&\bar{f}(\xi). \end{eqnarray*}

Thus $\bar{f}$ is unique.

In conclusion, the monotone determined cone $(CX, +, \cdot)$ is the monotone determined probabilistic powerspace of X, that is, $P_D(X)\cong (CX, +, \cdot)$ .

Remark 20. A related result is from Heckmann. It was shown that $\mathcal{V}_f(X)$ with weak topology is the free locally convex $T_0$ cone over X in TOP (Heckmann 1996, Theorem 7.6). The difference between our results is that the two topologies on $\mathcal{V}_f(X)$ are not the same generally.

The monotone determined probabilistic powerspace is unique up to algebraic isomorphism and topological homemorphism, so we can directly denote the monotone determined probabilistic powerspace by $P_D(X)=(CX, +, \cdot)$ for each monotone determined space X.

Suppose that X and Y are two monotone determined spaces and $f:X\rightarrow Y$ is a continuous map. Define the map $P_D(f):P_D(X)\rightarrow P_D(Y)$ as follows: $\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$ ,

\[P_D(f)(\xi)=\sum_{i=1}^{n}r_{b_i}\eta_{f(b_i)}.\]

$P_D(f)$ is well-defined and order preserving. It is also easy to check that, $P_D(f)$ is a monotone determined cone homomorphism between these two extended probabilistic powerspaces. If $id_X$ is the identity map and $g:Y\rightarrow Z$ is an arbitrary continuous map from Y to a monotone determined space Z, then, $P_D(id_X)=id_{P_D(X)},\ P_D(g\circ f)=P_D(g)\circ P_D(f)$ . Thus, $P_D:{\bf Dtop}\rightarrow {\bf Dscone}$ is a functor from Dtop to Dscone. Let $U:{\bf Dscone}\rightarrow {\bf Dtop}$ be the forgetful functor. By Theorem 19, we have the following result.

Corollary 21. $P_D$ is the left adjoint of the forgetful functor U, that is, Dscone is a reflective subcategory of Dtop.

Remark 22. Let X be a c-space, is $P_D(X)$ still a c-space? We will answer this question in the last section of this paper.

4. D-Completion and Free dcpo-cone over Any dcpo

Monotone convergence spaces (a.k.a d-spaces) form a very important class of $T_0$ topological spaces in domain theory. Interestingly, every $T_0$ space has a D-completion (See Definition 25). In this section, we will recall some notions about D-completions which are useful for our further discussions.

Definition 23. (Gierz et al. 2003,Definition II-3.12) Let X be a $T_0$ space. If X with the specialization order $(X,\leq)$ is a dcpo and every open set of X is Scott open in $(X,\leq)$ , then we call X a monotone convergence space.

A subset A of a poset P is called d-closed if for every directed subset D of A that possesses supremum $\bigvee D$ , $\bigvee D$ is included in A. The d-closed sets form the closed sets for a topology, called the d-topology (Keimel and Lawson 2009, Lemma 5.1). We denote the closure of A in P with d-topology by $\text{cl}_{d}(A)$ . If $\text{cl}_{d}(A)$ is equal to P, then we say that A is d-dense in P. A map f from a poset P to a poset Q is called d-continuous if f is continuous under the d-topology.

Lemma 24. (Keimel and Lawson 2009, Lemma 6.3) Consider the following properties for a subset A of a $T_0$ space X

1. (1) A is a monotone convergence space.

2. (2) A is a sub-dcpo.

3. (3) A is d-closed.

Then, (1) implies (2) and (2) implies (3), and all three are equivalent if X is a monotone convergence space.

Definition 25. (Keimel and Lawson 2009, Definition 6.5) An embedding $j\colon X\rightarrow\tilde{X}$ of a space X with image a d-dense subset of a monotone convergence space $\tilde{X}$ is called a D-completion.

The following result says that D-completions are universal, and hence, they are unique up to isomorphism.

Theorem . (Keimel and Lawson 2009, Theorem 6.7) Let $j\colon X\rightarrow Y$ be a topological embedding of a space X into a monotone convergence space Y. Let $\tilde{X}=\text{cl}_{d}(j(X))$ be the d-closure of j(X) in Y, equipped with the relative topology from Y. Then $k\colon X\rightarrow \tilde{X}$ , the co-restriction of j, is a universal D-completion, that is, for every continuous map f from X to a monotone convergence space M, there is a unique continuous map $\tilde{f}\colon\tilde{X}\rightarrow M$ such that $\tilde{f}\circ k=f$ .

Proposition 26. Let X be a $T_0$ space and $X^{d}$ be its D-completion. Then, $\mathcal{O}(X)\cong \mathcal{O}(X^{d})$ .

Proof. Let $f\colon X\rightarrow X^{s}$ be the soberification map. Since $X^{s}$ is sober, it is a monotone convergence space (Goubault-Larrecq 2013, Proposition 8.2.34), the D-completion $X^{d}$ of X can be regarded as a subspace of $X^{s}$ by Theorem 4. Then, $X^{s}$ is also a soberification of $X^{d}$ . We conclude that $\mathcal{O}(X)\cong \mathcal{O}(X^{d})$ directly.

Next we introduce the concept of Scott completion.

Definition 27. (Zhang et al. 2022, Definition 4.4) A Scott completion (Y, f) of a space X is a Scott space Y together with a continuous map $f\colon X\rightarrow Y$ such that for any Scott space Z and continuous map $g\colon X\rightarrow Z$ , there exists a unique continuous map $\tilde{g}$ satisfying $g =\tilde{g}\circ f$ .

Not every space has a Scott completion (see the following Example 28). An alternative argument is that the category of Scott space with continuous maps is not reflective in the category of $T_0$ spaces, we refer to Sheng et al. (2023, Theorem 3.6).

Example 28 Let $\mathbb{N}$ be the set of natural numbers endowed with co-finite topology.

Claim: $\mathbb{N}$ does not have a Scott completion. To obtain a contradiction, assume that $\mathbb{N}$ has a Scott completion $(\bar{\mathbb{N}},f)$ , where f is a continuous map from $\mathbb{N}$ to the Scott space $\bar{\mathbb{N}}$ .

1. (1) f is injective.

For any two different numbers n and m, consider the Sierpinski space $\mathbb{S}$ which is the poset $\{\bot,\top\} (\bot<\top)$ equipped with its Scott topology. Define a continuous map $g\colon\mathbb{N}\rightarrow\mathbb{S}$ as follows: $g(n)=\bot, g(x)=\top $ for any $x\neq n$ . Since $(\bar{\mathbb{N}},f)$ is a Scott completion, there is a continuous map $\tilde{g}\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$ such that $\tilde{g}\circ f=g$ . It follows that $\tilde{g}(f(n))=g(n)=\bot, \tilde{g}(f(m))=g(m)=\top$ . Hence, $f(n)\neq f(m)$ .

1. (2) For any two different numbers n,m of $\mathbb{N}$ , f(n) and f(m) are incomparable in $\bar{\mathbb{N}}$ .

Without loss of generality, we assume that $f(m)<f(n)$ . By the same argument of the first step, $\top=g(m)=\tilde{g}(f(m))\leq\tilde{g}(f(n))=g(n)=\bot$ , a contradiction.

1. (3) For any $x\in\bar{\mathbb{N}}, $ there is some $n\in\mathbb{N}$ such that $f(n)\leq x$ . In other words, ${\downarrow}x\cap f(\mathbb{N})\neq\emptyset$ . To obtain a contradiction, suppose there is some $x_0\in\bar{\mathbb{N}}$ with ${\downarrow}x_0\cap f(\mathbb{N})=\emptyset$ . We take a constant map $g=\lambda n.\top\colon\mathbb{N}\rightarrow\mathbb{S}$ . Clearly, it is continuous. Now let us consider two continuous maps $g_1, g_2\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$ as follows:

   \[g_1(x)=\top,\forall x;\]

\[g_2(x)= \begin{cases} \top, & x\not\leq x_0,\\ \bot, & x \leq x_0. \end{cases}\]

It is easy to verify that $g=g_1\circ f=g_2\circ f$ , which contradicts the uniqueness of $\tilde{g}$ .

We conclude that $f(\mathbb{N})$ is the set of minimal elements of $\bar{\mathbb{N}}$ from (1), (2) and (3). Notice that every subset A of $f(\mathbb{N})$ is Scott closed in $\bar{\mathbb{N}}$ . Hence, $f(\mathbb{N})$ with its subspace topology of $\bar{\mathbb{N}}$ is a discrete space. It follows that $f^{-1}(A)$ is closed in $\mathbb{N}$ for any $A\subseteq f(X)$ . We see at once that $\mathbb{N}$ is a discrete space as well, a contradiction.

But any poset with Scott topology has a Scott completion (Keimel and Lawson 2009) and the following result tells us that every monotone determined space has a Scott completion. Let X be a monotone determined space. The map $i\colon X\rightarrow \Gamma X$ is defined by $i(x)={\downarrow}x$ , where $\Gamma X$ is the lattice of closed subsets of X. We denote the d-closure of $i(X)=\{{\downarrow}x:x\in X\}$ in $\Gamma X$ by $\tilde{X}$ . The map $i\colon X\rightarrow\tilde{X}$ has the universal property: For any Scott space Z and any continuous map $f\colon X\rightarrow Z$ , there is a unique Scott continuous map $\bar{f}\colon\tilde{X}\rightarrow Z$ which is defined by $\bar{f}(A)=\bigvee\text{cl}_{\sigma}(f(A))$ , such that $f=\bar{f}\circ i$ .

Theorem 29. (Zhang et al. 2022, Theorem 4.7) Let X be a monotone determined space. Then, $(\tilde{X},i)$ is a Scott completion of X, which we call the standard Scott completion.

Remark 30. Let X be a monotone determined space. The Scott completion of X is just the D-completion of X because the D-completion of X is a Scott space. An interesting question is: the D-completions of which kind of $T_0$ spaces are Scott spaces.

Next, we will recall some basic properties of dcpo-cones. As far as we know, there is no representation of free dcpo-cone over general dcpos. In this section, we will construct the free dcpo-cone over any dcpo by using the Scott completion of a monotone determined space.

Definition 31. (Gierz et al. 2003, Definition IV-9.20) A dcpo-cone is a dcpo C equipped with a distinguished element $0\in C$ , an addition $+:C\times C\rightarrow C$ which is Scott continuous, and a scalar multiplication $\cdot:\mathbb{R}^{+}\times C\rightarrow C$ which is Scott continuous, such that the usual axioms of a vector space hold, except for the existence of an additive inverse (in this case, one also assumes that $0\cdot a=0$ for any $a\in C$ .)

Definition 32. Let C,D be two dcpo-cones. A map $f\colon C\rightarrow D$ is said to be linear if

\[f(r\cdot a)=rf(a), \text{for all } r\in\mathbb{R^+} \text{and } a\in C\]

and

\[f(a+b)=f(a)+f(b), \text{for all} a,b\in C.\]

Let Dcone denote the category of dcpo-cones with Scott continuous linear maps.

Lemma 33. (Keimel and Lawson 2012, Lemma 3.4) Let $f\colon\prod_{i=1}^{n}X_i\rightarrow Y$ be separately continuous. Then for arbitrary nonempty subsets, $A_i\subseteq X_i$ for $1\leq i\leq n$ and $B\subseteq Y:$

1. (1) $f(\prod_{i=1}^{n}\bar{A_i})\subseteq\bar{B}$ whenever $f(\prod_{i=1}^{n}A_i)\subseteq B$ ;

2. (2) $\overline{f(\prod_{i=1}^{n}\bar{A_i})}=\overline{f(\prod_{i=1}^{n}A_i)}$ ;

3. (3) $f^{\gamma}\colon\prod_{i=1}^{n}\Gamma X_i\rightarrow\Gamma Y$ is separately continuous, hence Scott continuous. Here the definition of $f^{\gamma}$ is as follows:

   \[f^{\gamma}(A_1,\cdots,A_n)=\overline{f\left(\prod_{i=1}^{n}A_i\right)}=\overline{\{f(x_1,\cdots,x_n):x_i\in A_i \text{for} 1\leq i\leq n\}}.\]

Definition 34. Let X be a monotone determined cone. We denote the Scott completion of X by $\tilde{X}$ . For any $A,B\in \Gamma X$ , we define $A\oplus B=\text{cl}\{a+b:a\in A,b\in B\}$ , $r\odot A=\{ra:a\in A\}$ for all $r\in\mathbb{R^+}$ .

Next we will verify that $\tilde{X}$ with these two operations is a dcpo-cone.

Lemma 35. Let X be a monotone determined cone. The Scott completion $(\tilde{X},\oplus,\odot)$ is a dcpo-cone.

Proof. It is easy to see that $X\rightarrow\tilde{X}$ is a linear map. First, we show that $\oplus\colon\tilde{X}\times\tilde{X}\rightarrow\tilde{X}$ is a well-defined Scott continuous map. By Lemma 33(3), $\oplus\colon\Gamma X\times\Gamma X\rightarrow\Gamma X$ is Scott continuous, hence d-continuous. For any $A \in\tilde{X}$ , we consider a map $g\colon\Gamma X\rightarrow\Gamma X, g(F)=A\oplus F, \forall F\in\Gamma X$ . Since g is d-continuous,

\[\forall B\in\tilde{X}: A\oplus B\in g(cl_{d}\{{\downarrow}x:x\in X\})\subseteq cl_{d}(\{A\oplus{\downarrow}x:x\in X\}).\]

Next we consider another map $h\colon\Gamma X\rightarrow\Gamma X, h(F)=F\oplus{\downarrow}y$ for a given $y\in X$ .

Hence, we obtain that $A\oplus B\in\tilde{X}$ .

Second for any $A,B,C\in\Gamma X$ , obviously $A\oplus B=B\oplus A$ , $A\oplus {\downarrow}0=A$ , and:

\begin{align*}\overline{\{a+b+c:a\in A,b\in B,c\in C\}}&\subseteq A\oplus(B\oplus C)\\ &=\overline{\{a+x:a\in A,x\in B\oplus C\}}\\ &=\overline{\bigcup_{a\in A}\{a+x:x\in B\oplus C\}}\\ &\subseteq\overline{\bigcup_{a\in A}cl\{a+(b+c):b\in B,c\in C\}} (\lambda x.a+x\colon X\rightarrow X \text{is continuous})\\ &\subseteq \overline{\{a+b+c:a\in A,b\in B,c\in C\}}\end{align*}

Thus, we have $A\oplus (B\oplus C)=\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$ . For the same reason, $(A\oplus B)\oplus C$ is equal to $\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$ . Therefore, $(A\oplus B)\oplus C=A\oplus (B\oplus C)$ .

For any positive real number r, the map $\lambda x.rx\colon X\rightarrow X$ is a homomorphism. Hence, $r\odot F=\{ra:a\in F\}\in\Gamma X$ for each $F\in\Gamma X$ . Note that the map $f=\lambda F.r\odot F\colon\Gamma X\rightarrow\Gamma X$ is an order isomorphism under the inclusion ordering. For any $A\in\tilde{X}$ ,

Therefore, the map $\lambda A.r\odot A\colon\tilde{X}\rightarrow\tilde{X}$ is well-defined and Scott continuous.

Given any non-negative real numbers r,s and $A,B\in\tilde{X}$ ,learly

\[1\odot A=A, 0\odot A={\downarrow}0, (rs)\odot A=r\odot (s\odot A),\]

and

\[r\odot (A\oplus B)=r\odot\overline{\{a+b:a\in A,b\in B\}}=\overline{\{ra+rb:a\in A,b\in B\}}=(r\odot A)\oplus (r\odot B).\]

Next we show that

\[(r+s)\odot A=(r\odot A)\oplus (s\odot A).\]

If $A={\downarrow}x$ for some $x\in X$ , then $(r+s)\odot{\downarrow}x={\downarrow}(r+s)x$ and $(r\odot{\downarrow}x)\oplus (s\odot{\downarrow}x)$ = $\overline{\{ra+sb:a\leq x,b\leq x\}}={\downarrow}(r+s)x$ . We set $\mathcal{S}:=\{C\in\Gamma X:(r+s)\odot C=(r\odot C)\oplus (s\odot C)\}$ . By the preceding argument, $\{{\downarrow}x:x\in X\}\subseteq\mathcal{S}$ . For any directed family $\{A_i:i\in I\}$ of $\mathcal{S}$ ,

It is easy to see that

\[(r+s)\odot\bigvee_{i\in I}A_i\subseteq(r\odot\bigvee_{i\in I}A_i)\oplus (s\odot\bigvee_{i\in I}A_i).\]

It follows that $\bigvee_{i\in I}A_i\in\mathcal{S}$ . Hence, we have $A\in\tilde{X}\subseteq\mathcal{S}$ .

Finally, for any fixed $A\in\tilde{X}, g=\lambda x.x\odot A\colon\mathbb{R^+}\rightarrow\tilde{X}$ is Scott continuous. Since $\lambda x.xa\colon \mathbb{R^+}\rightarrow X$ is continuous for each $a\in X$ , then g is monotone. Given any bounded directed set $\{x_i:i\in I\}\subseteq\mathbb{R^+}$ , $(\bigvee_{i\in I}^{\uparrow}x_i)\odot A=\{(\bigvee_{i\in I}^{\uparrow}x_i)a:a\in A\}=\{\bigvee_{i\in I}^{\uparrow}x_ia:a\in A\}\subseteq \overline{\bigcup_{i\in I}^{\uparrow}x_i\odot A}=\bigvee_{i\in I}^{\uparrow}(x_i\odot A)$ . It is easily seen that $\bigvee_{i\in I}^{\uparrow}(x_i\odot A)\subseteq(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$ . We conclude that $\bigvee_{i\in I}^{\uparrow}(x_i\odot A)=(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$ . Therefore $(\tilde{X},\oplus,\odot)$ is a dcpo-cone.

Next we give the construction of free dcpo-cone over any dcpo by using the D-completions. It is one of the main results of this paper.

Theorem 36. Let D be a dcpo. The standard Scott completion $\big( (\mathfrak{D},\oplus,\odot),i\big)$ of $P_D(\Sigma D)$ is the free dcpo-cone, that is, given any dcpo-cone $\mathfrak{E}$ and any Scott continuous map $f\colon D\rightarrow\mathfrak{E}$ , if we assign $\xi=i\circ\eta'\colon D\rightarrow$ $\mathfrak{D}$ , where $\forall d\in D:$ $\eta'(d)=\eta_{d}$ . Then, there is a unique Scott continuous linear map $\bar{f}\colon\mathfrak{D}\rightarrow\mathfrak{E}$ such that $\bar{f}\circ\xi=f$ .

Proof. Since $\mathfrak{E}$ is a dcpo-cone, it is also a monotone determined cone with respect to Scott topology. Because $P_D(\Sigma D)$ is the free monotone determined cone over $\Sigma D$ , there exists a unique continuous linear map $\hat{f}\colon P_D(\Sigma D)\rightarrow \mathfrak{E}$ such that $\hat{f}\circ\eta'=f$ . By a similar argument, there is a unique continuous map $\bar{f}\colon\mathfrak{D}\rightarrow \mathfrak{E}$ with $\bar{f}\circ i=\hat{f}$ . We claim that $\bar{f}$ is also a linear map between $\mathfrak{D}$ and $\mathfrak{E}$ . For any element $F\in\mathfrak{D}$ , $\bar{f}(F)=\bigvee\overline{\hat{f}(F)}$ . Given any $\lambda\in\mathbb{R^+}$ , $\bar{f}(\lambda\odot F)=\bigvee\overline{\hat{f}(\lambda\odot F)}=\bigvee\overline{\lambda\odot\hat{f}(F)}=\bigvee(\lambda\overline{\hat{f}(F)})=\lambda\cdot\bigvee(\overline{\hat{f}(F)})=\lambda\cdot\bar{f}(F)$ . For any $A,B\in\mathcal{F}$ , we calculate

Suppose that there is another Scott continuous linear map $g\colon\mathfrak{D}\rightarrow\mathfrak{E}$ such that $g\circ\xi=f$ . Set $S=\{x\in\mathfrak{D}:\bar{f}(x)=g(x)\}$ . Clearly, S is closed under addition and scalar multiplication. Because $\bar{f}$ and g are Scott continuous, S is also a sub-dcpo of $\mathfrak{D}$ . It is easy to see that for any $d\in D$ , $\xi(d)\in S$ . Since i preserves multiplication, $i(r\cdot\eta_{d})=r\odot (i\circ\eta'(d))=r\odot\xi(d)\in S$ . By the additivity of i, $i(a)\in S$ for any $a\in P_D(\Sigma D)$ . Hence, S is equal to $\mathfrak{D}$ because the image of i is d-dense in $\mathfrak{D}$ . Consequently $\bar{f}=g$ .

Remark 37. By the above argument, we have actually shown that the standard Scott-completion functor $\colon \textbf{Dscone}\rightarrow\textbf{Dcone}$ is the left adjoint of the forgetful functor. Jia and Mislove (2022) have considered the D-completion of $\mathcal{V}_f(X)$ with the weak topology and dcpo completion of the poset $\mathcal{V}_{f}(X)$ , which are different from our construction due to the different topology on $\mathcal{V}_{f}(X)$ .

5. Valuation Power domain and Free dcpo-cone

A well-known result in probabilistic power domain theory is that the space of continuous valuations over $\Sigma D$ is the free dcpo-cone of $\Sigma D$ if D is a continuous domain (Gierz et al. 2003, Theorem IV-9.24). But it is unknown whether this result still holds for the case of general dcpos. In this section, we will discuss this problem and build some relationships between the space of valuations and the free dcpo-cones for more general dcpos instead of continuous ones.

In the following, we introduce some notations. Let F(D) denote the free dcpo-cone over D if D is a dcpo. For a topological space X, the valuation power domain (also called the extended probabilistic power domain) $\mathcal{V}(X)$ of X is the set of all continuous valuations on $\mathcal{O}(X)$ with the pointwise order, sometimes called the stochastic order: $\mu\leq\nu$ iff $\mu(U)\leq\nu(U)$ for all open sets U.

Theorem 38. (Gierz et al. 2003, Theorem IV-9.24) Given any dcpo-cone C and a continuous map $f:X\rightarrow C$ , where X is a domain equipped with the Scott topology, there exists a unique continuous linear map $f^{\ast}:\mathcal{V}(X)\rightarrow C$ such that $f^{\ast}\eta_X=f$ , here $\eta_X(x)=\eta_x,\ \forall x\in X$ .

Let D be a domain. The extension map $\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$ is a D-completion map. The topology on $P_D(\Sigma D)$ is the subspace topology induced by the Scott topology on $\mathcal{V}(D)$ .

Proof. By Theorem 38 $(\mathcal{V}(D),\eta)$ is the free dcpo-cone over continuous dcpo D. Applying Theorem 36 to this case, the map $\bar{\eta}\colon\mathcal{D}\rightarrow\mathcal{V}(D)$ is an isomorphism between d-cones.

Clearly, the map $\bar{\eta}\colon \Sigma(\mathcal{D})\rightarrow\Sigma(\mathcal{V}(D))$ is also a topological isomorphism. Notice that $i\colon P_D(\Sigma D)\rightarrow\mathcal{D}$ is a D-completion map. It follows that $\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$ is a D-completion map. Hence, the topology of $P_D(\Sigma D)$ is the subspace topology induced by the Scott topology on $\mathcal{V}(D)$ .

Corollary 40. Let X be a c-space. The powerspace $P_D(X)$ is also a c-space.

Proof. $X^{d}$ is a c-space by Propositions 6 and 26. Hence, $X^{d}$ with specialization order is a domain. Using the universal properties of D-completion on monotone determined spaces and $\mathcal{V}$ on domains, $\mathcal{V}(X^d)$ is the free dcpo-cone over X. Similar arguments tell us that $P_D^{d}(X)$ is also the free dcpo-cone over X. Since $\mathcal{V}(X^d)$ is a continuous dcpo, then $P_D^{d}(X)\cong\mathcal{V}(X^d)$ is a c-space. Again by Propositions 6 and 26, we have that $P_D(X)$ is also a c-space.

Proposition 41. Let X be a topological space. $\mathcal{V}_{p}(X)$ (the set of point-continuous valuations, see Definition 8) with the usual addition and scalar multiplication is a dcpo-cone.

Proof. It is easy to see that $\mathcal{V}_{p}(X)$ is a dcpo with the pointwise order and the supremum of a directed family $\{\mu_i:i\in I\}$ of point-continuous valuations is $\mu=\lambda U.\bigvee_{i\in I}^{\uparrow}\mu_i(U)$ for any $U\in\mathcal{O}(X)$ .

We first show that $\mathcal{V}_{p}(X)$ is closed under addition. Given any two point-continuous valuations $\mu_1,\mu_2$ , for any $r\in \bar{\mathbb{R}}^{+}$ and $U\in\mathcal{O}(X)$ , assume that $\mu_1(U)+\mu_2(U)>r$ . If one of $\mu_1(U)$ and $\mu_2(U)$ is equal to 0, without loss of generality we say $\mu_1(U)=0$ , then $\mu_2(U)>r$ . Since $\mu$ is point-continuous, there is a finite subset F of U such that $\mu_2(V)>r$ for any open set $V\supseteq F$ . It follows that $\mu_1(V)+\mu_2(V)>r$ for any open set $V\supseteq F$ . Another case is that neither of $\mu_1(U)$ nor $\mu_2(U)$ is equal to 0. Take a positive real number $\epsilon$ such that $\epsilon<\mu_1(U), \epsilon<\mu_2(U), \mu_1(U)-\epsilon+\mu_2(U)-\epsilon>r$ . By the point continuity of $\mu_i$ (i=1,2), there is a finite set $F_i\subseteq U$ satisfying $\mu_i(V)>\mu_i(U)-\epsilon$ for any open set $V\supseteq F_i$ . Let F be the union of $F_1$ and $F_2$ , clearly $\mu_1(V)+\mu_2(V)>r$ for any open set $V\supseteq F$ . We conclude that $\mu_1+\mu_2\in\mathcal{V}_{p}(X)$ .

It is easily seen that $\mathcal{V}_{p}(X)$ is closed under scalar multiplication. It is a routine to check that $\cdot\colon\mathbb{R}^{+}\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$ and $+\colon\mathcal{V}_{p}(X)\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$ are Scott continuous. Hence, $\mathcal{V}_{p}(X)$ is a dcpo-cone.

Example 42. Let D be the Smyth power domain ( $\mathcal{Q}(\mathbb{R}_{\ell}))$ of the Sorgenfrey line $\mathbb{R}_{\ell}$ . By the result of Goubault and Jia (2021, Theorem 39), the inclusion map $j\colon\mathcal{V}_{p}(D)\rightarrow\mathcal{V}(D)$ is not surjective. We claim that $(\mathcal{V}(D),\eta)$ is not the free dcpo-cone over D. Let $(F(D),\xi)$ be the free dcpo-cone over D and $\eta_1$ the co-restriction of $\eta\colon D\rightarrow\mathcal{V}(D)$ on $\mathcal{V}_{p}(D)$ . Obviously $\eta=j\circ\eta_1$ . By the universal property of F(D), there is a unique Scott continuous linear map f with $\eta_{1}=f\circ\xi$ . Let g denote the map $j\circ f$ , then $g\circ\xi=(j\circ f)\circ\xi=j\circ(f\circ\xi)=j\circ\eta_1=\eta$ . Clearly g is a Scott continuous linear map but not surjective. Hence, $(\mathcal{V}(D),\eta)$ is not a free dcpo-cone over D.

Remark 43. In the future, we plan to discuss the relations between the free dcpo-cone over a general (quasicontinuous) dcpo D and the space of minimal valuations over D (Goubault and Jia 2021).