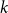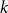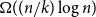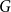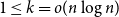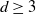Random walks on graphs are an essential primitive for many randomised algorithms and stochastic processes. It is natural to ask how much can be gained by running
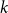 $k$
multiple random walks independently and in parallel. Although the cover time of multiple walks has been investigated for many natural networks, the problem of finding a general characterisation of multiple cover times for worst-case start vertices (posed by Alon, Avin, Koucký, Kozma, Lotker and Tuttle in 2008) remains an open problem. First, we improve and tighten various bounds on the stationary cover time when
$k$
multiple random walks independently and in parallel. Although the cover time of multiple walks has been investigated for many natural networks, the problem of finding a general characterisation of multiple cover times for worst-case start vertices (posed by Alon, Avin, Koucký, Kozma, Lotker and Tuttle in 2008) remains an open problem. First, we improve and tighten various bounds on the stationary cover time when
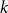 $k$
random walks start from vertices sampled from the stationary distribution. For example, we prove an unconditional lower bound of
$k$
random walks start from vertices sampled from the stationary distribution. For example, we prove an unconditional lower bound of
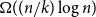 $\Omega ((n/k) \log n)$
on the stationary cover time, holding for any
$\Omega ((n/k) \log n)$
on the stationary cover time, holding for any
 $n$
-vertex graph
$n$
-vertex graph
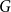 $G$
and any
$G$
and any
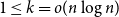 $1 \leq k =o(n\log n )$
. Secondly, we establish the stationary cover times of multiple walks on several fundamental networks up to constant factors. Thirdly, we present a framework characterising worst-case cover times in terms of stationary cover times and a novel, relaxed notion of mixing time for multiple walks called the partial mixing time. Roughly speaking, the partial mixing time only requires a specific portion of all random walks to be mixed. Using these new concepts, we can establish (or recover) the worst-case cover times for many networks including expanders, preferential attachment graphs, grids, binary trees and hypercubes.
$1 \leq k =o(n\log n )$
. Secondly, we establish the stationary cover times of multiple walks on several fundamental networks up to constant factors. Thirdly, we present a framework characterising worst-case cover times in terms of stationary cover times and a novel, relaxed notion of mixing time for multiple walks called the partial mixing time. Roughly speaking, the partial mixing time only requires a specific portion of all random walks to be mixed. Using these new concepts, we can establish (or recover) the worst-case cover times for many networks including expanders, preferential attachment graphs, grids, binary trees and hypercubes.