Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T14:57:46.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Cover time for branching random walks on regular trees

Part of: Geometric probability and stochastic geometry Markov processes

Published online by Cambridge University Press:  09 February 2022

Matthew I. Roberts Open the ORCID record for Matthew I. Roberts [Opens in a new window]
Matthew I. Roberts*
Affiliation:
University of Bath
*
*Postal address: Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK. Email address: mattiroberts@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let T be the regular tree in which every vertex has exactly 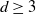$d\ge 3$ neighbours. Run a branching random walk on T, in which at each time step every particle gives birth to a random number of children with mean d and finite variance, and each of these children moves independently to a uniformly chosen neighbour of its parent. We show that, starting with one particle at some vertex 0 and conditionally on survival of the process, the time it takes for every vertex within distance r of 0 to be hit by a particle of the branching random walk is 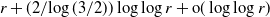$r + ({2}/{\log(3/2)})\log\log r + {\mathrm{o}}(\log\log r)$ .

Keywords

Branching random walktreecover timerightmost particle

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60D05: Geometric probability and stochastic geometry
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 1 , March 2022 , pp. 256 - 277
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidekon, E. (2013). Convergence in law of the minimum of a branching random walk. Ann. Prob. 41,1362–1426.CrossRefGoogle Scholar
Benjamini, I. and Peres, Y. (1994). Markov chains indexed by trees. Ann. Prob. 22, 219–243.10.1214/aop/1176988857CrossRefGoogle Scholar
Benjamini, I. and Schramm, O. (1997). Every graph with a positive Cheeger constant contains a tree with a positive Cheeger constant. Geom. Funct. Anal. 7, 403–419.CrossRefGoogle Scholar
Biggins, J. D. (1976). The first- and last-birth problems for a multitype age-dependent branching process. Adv. Appl. Prob. 8, 446–459.CrossRefGoogle Scholar
Biggins, J. D. (1977). Chernoff’s theorem in the branching random walk. J. Appl. Prob. 14, 630–636.CrossRefGoogle Scholar
Biggins, J. D. (1978). The asymptotic shape of the branching random walk. Adv. Appl. Prob. 10, 62–84.CrossRefGoogle Scholar
Bramson, M. D. (1978). Maximal displacement of branching Brownian motion. Commun. Pure Appl. Math. 31, 531–581.CrossRefGoogle Scholar
Bramson, M. D. (1978). Minimal displacement of branching random walk. Z. Wahrscheinlichkeitsth. 45, 89–108.10.1007/BF00715186CrossRefGoogle Scholar
Bramson, M. D., Ding, J. and Zeitouni, O. (2016). Convergence in law of the maximum of nonlattice branching random walk. Ann. Inst. H. Poincaré Prob. Statist. 52, 1897–1924.CrossRefGoogle Scholar
Fortuin, C., Kasteleyn, P. and Ginibre, J. (1971). Correlation inequalities on some partially ordered sets. Commun. Math. Phys. 22, 89–103.CrossRefGoogle Scholar
Gantert, N. and Müller, S. (2006). The critical branching Markov chain is transient. Markov Process. Relat. Fields 12, 805–814.Google Scholar
Hammersley, J. M. (1974). Postulates for subadditive processes. Ann. Prob. 2, 652–680.CrossRefGoogle Scholar
Kesten, H. and Stigum, B. P. (1966). A limit theorem for multidimensional Galton–Watson processes. Ann. Math. Statist. 37, 1211–1223.CrossRefGoogle Scholar
Kingman, J. (1975). The first birth problem for an age-dependent branching process. Ann. Prob. 3, 790–801.CrossRefGoogle Scholar
Kolmogorov, A. N. (1938). On the solution of a biological problem. Proc. Tomsk University 2, 7–12.Google Scholar
Liggett, T. (1996). Branching random walks and contact processes on homogeneous trees. Prob. Theory Relat. Fields 106, 495–519.CrossRefGoogle Scholar
Lyons, R. and Peres, Y. (2016). Probability on Trees and Networks (Cambridge Series in Statistical and Probabilistic Mathematics 42). Cambridge University Press, New York.CrossRefGoogle Scholar
Madras, N. and Schinazi, R. (1992). Branching random walks on trees. Stoch. Process. Appl. 42, 255–267.CrossRefGoogle Scholar
Pakes, A. G. (1971). Some limit theorems for the total progeny of a branching process. Adv. Appl. Prob. 3, 176–192.CrossRefGoogle Scholar
Pemantle, R. and Stacey, A. M. (2001). The branching random walk and contact process on Galton–Watson and nonhomogeneous trees. Ann. Prob. 29, 1563–1590.10.1214/aop/1015345762CrossRefGoogle Scholar
Sudakov, B. and Vondrák, J. (2007). Nearly optimal embeddings of trees. Available at arXiv:0707.2079.Google Scholar