1 results
d-Auslander–Reiten sequences in subcategories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 15 January 2020, pp. 342-373
-
- Article
- Export citation
-
Let Φ be a finite-dimensional algebra over a field k. Kleiner described the Auslander–Reiten sequences in a precovering extension closed subcategory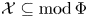
${\rm {\cal X}}\subseteq {\rm mod }\,\Phi $. If 
$X\in \mathcal {X}$ is an indecomposable such that 
${\rm Ext}_\Phi ^1 (X,{\rm {\cal X}})\ne 0$ and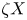 
$\zeta X$ is the unique indecomposable direct summand of the 
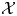$\mathcal {X}$-cover 
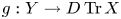$g:Y\to D\,{\rm Tr}\,X$ such that 
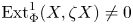${\rm Ext}_\Phi ^1 (X,\zeta X)\ne 0$, then there is an Auslander–Reiten sequence in 
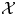$\mathcal {X}$ of the form
Moreover, when
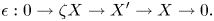$${\rm \epsilon }:0\to \zeta X\to {X}^{\prime}\to X\to 0.$$
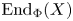${\rm En}{\rm d}_\Phi (X)$ modulo the morphisms factoring through a projective is a division ring, Kleiner proved that each non-split short exact sequence of the form
is such that η is right almost split in
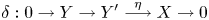$$\delta :0\to Y\to {Y}^{\prime}\buildrel \eta \over \longrightarrow X\to 0$$
$\mathcal {X}$, and the pushout of δ along g gives an Auslander–Reiten sequence in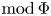 
${\rm mod}\,\Phi $ ending at X.In this paper, we give higher-dimensional generalizations of this. Let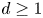
$d\geq 1$ be an integer. A d-cluster tilting subcategory 
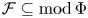${\rm {\cal F}}\subseteq {\rm mod}\,\Phi $ plays the role of a higher 
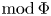${\rm mod}\,\Phi $. Such an 
$\mathcal {F}$ is a d-abelian category, where kernels and cokernels are replaced by complexes of d objects and short exact sequences by complexes of d + 2 objects. We give higher versions of the above results for an additive ‘d-extension closed’ subcategory 
$\mathcal {X}$ of 
$\mathcal {F}$.
