d-Auslander–Reiten sequences in subcategories

Abstract

Let Φ be a finite-dimensional algebra over a field k. Kleiner described the Auslander–Reiten sequences in a precovering extension closed subcategory 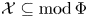${\rm {\cal X}}\subseteq {\rm mod }\,\Phi $. If 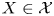$X\in \mathcal {X}$ is an indecomposable such that ${\rm Ext}_\Phi ^1 (X,{\rm {\cal X}})\ne 0$ and 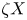$\zeta X$ is the unique indecomposable direct summand of the 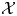$\mathcal {X}$-cover 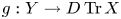$g:Y\to D\,{\rm Tr}\,X$ such that 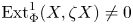${\rm Ext}_\Phi ^1 (X,\zeta X)\ne 0$, then there is an Auslander–Reiten sequence in 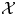$\mathcal {X}$ of the form

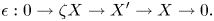$${\rm \epsilon }:0\to \zeta X\to {X}^{\prime}\to X\to 0.$$

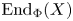Moreover, when ${\rm En}{\rm d}_\Phi (X)$ modulo the morphisms factoring through a projective is a division ring, Kleiner proved that each non-split short exact sequence of the form

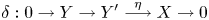$$\delta :0\to Y\to {Y}^{\prime}\buildrel \eta \over \longrightarrow X\to 0$$

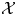is such that η is right almost split in $\mathcal {X}$, and the pushout of δ along g gives an Auslander–Reiten sequence in 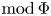${\rm mod}\,\Phi $ ending at X.

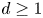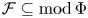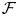In this paper, we give higher-dimensional generalizations of this. Let $d\geq 1$ be an integer. A d-cluster tilting subcategory ${\rm {\cal F}}\subseteq {\rm mod}\,\Phi $ plays the role of a higher ${\rm mod}\,\Phi $. Such an $\mathcal {F}$ is a d-abelian category, where kernels and cokernels are replaced by complexes of d objects and short exact sequences by complexes of d + 2 objects. We give higher versions of the above results for an additive ‘d-extension closed’ subcategory 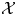$\mathcal {X}$ of 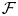$\mathcal {F}$.