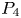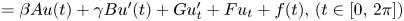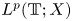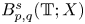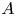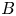In this paper, we mainly investigate the well-posedness of the four-order degenerate differential equation ($P_4$): $(Mu)''''(t) + \alpha (Lu)'''(t) + (Lu)''(t)$ $=\beta Au(t) + \gamma Bu'(t) + Gu'_t + Fu_t + f(t),\,( t\in [0,\,2\pi ])$ in periodic Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$ and periodic Besov spaces $B_{p,q}^s\;(\mathbb {T}; X)$, where $A$, $B$, $L$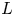 and $M$ 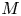are closed linear operators on a Banach space $X$ such that $D(A)\cap D(B)\subset D(M)\cap D(L)$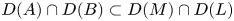 and $\alpha,\,\beta,\,\gamma \in \mathbb {C}$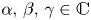, $G$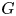 and $F$ 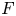are bounded linear operators from $L^p([-2\pi,\,0];X)$ (respectively $B_{p,q}^s([-2\pi,\,0];X)$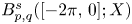) into $X$, $u_t(\cdot ) = u(t+\cdot )$ 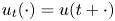and $u'_t(\cdot ) = u'(t+\cdot )$ 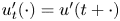are defined on $[-2\pi,\,0]$ for $t\in [0,\, 2\pi ]$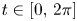. We completely characterize the well-posedness of ($P_4$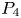) in the above two function spaces by using known operator-valued Fourier multiplier theorems.

In this paper, by using operator-valued ${\dot{C}}^{\unicode[STIX]{x1D6FC}}$-Fourier multiplier results on vector-valued Hölder continuous function spaces, we give a characterization of the $C^{\unicode[STIX]{x1D6FC}}$-well-posedness for the third order differential equations $au^{\prime \prime \prime }(t)+u^{\prime \prime }(t)=Au(t)+Bu^{\prime }(t)+f(t)$, ($t\in \mathbb{R}$), where $A,B$ are closed linear operators on a Banach space $X$ such that $D(A)\subset D(B)$, $a\in \mathbb{C}$ and $0<\unicode[STIX]{x1D6FC}<1$.

Using known operator-valued Fourier multiplier results on vector-valued Hölder continuous function spaces ${{C}^{\alpha }}(\mathbb{R};\,X)$, we completely characterize the ${{C}^{\alpha }}$-well-posedness of the first order degenerate differential equations with finite delay $(Mu{)}'(t)\,=\,Au(t)\,+\,F{{u}_{t}}\,+\,f(t)$ for $t\,\in \,\mathbb{R}$ by the boundedness of the $(M,\,F)$-resolvent of A under suitable assumption on the delay operator $F$, where $A,M$ are closed linear operators on a Banach space $X$ satisfying $D(A)\,\cap \,D(M)\,\ne \,\{0\}$, the delay operator $F$ is a bounded linear operator from $C([-r,0];X)$ to $X$, and $r\,>\,0$ is fixed.