No CrossRef data available.
Article contents
Hölder Continuous Solutions of Degenerate Differential Equations with Finite Delay
Published online by Cambridge University Press: 20 November 2018
Abstract
Using known operator-valued Fourier multiplier results on vector-valued Hölder continuous function spaces 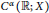 ${{C}^{\alpha }}(\mathbb{R};\,X)$, we completely characterize the
${{C}^{\alpha }}(\mathbb{R};\,X)$, we completely characterize the 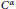 ${{C}^{\alpha }}$-well-posedness of the first order degenerate differential equations with finite delay
${{C}^{\alpha }}$-well-posedness of the first order degenerate differential equations with finite delay 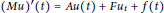 $(Mu{)}'(t)\,=\,Au(t)\,+\,F{{u}_{t}}\,+\,f(t)$ for
$(Mu{)}'(t)\,=\,Au(t)\,+\,F{{u}_{t}}\,+\,f(t)$ for 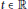 $t\,\in \,\mathbb{R}$ by the boundedness of the
$t\,\in \,\mathbb{R}$ by the boundedness of the 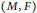 $(M,\,F)$-resolvent of A under suitable assumption on the delay operator
$(M,\,F)$-resolvent of A under suitable assumption on the delay operator 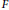 $F$, where
$F$, where 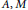 $A,M$ are closed linear operators on a Banach space
$A,M$ are closed linear operators on a Banach space 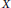 $X$ satisfying
$X$ satisfying 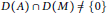 $D(A)\,\cap \,D(M)\,\ne \,\{0\}$, the delay operator
$D(A)\,\cap \,D(M)\,\ne \,\{0\}$, the delay operator 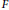 $F$ is a bounded linear operator from
$F$ is a bounded linear operator from 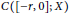 $C([-r,0];X)$ to
$C([-r,0];X)$ to 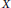 $X$, and
$X$, and 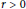 $r\,>\,0$ is fixed.
$r\,>\,0$ is fixed.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018


