We prove the Bernoulli property for determinantal point processes on
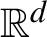 \mathbb{R}^d
with translation-invariant kernels. For the determinantal point processes on
\mathbb{R}^d
with translation-invariant kernels. For the determinantal point processes on
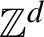 \mathbb{Z}^d
with translation-invariant kernels, the Bernoulli property was proved by Lyons and Steif [Stationary determinantal processes: phase multiplicity, bernoullicity, and domination. Duke Math. J.120 (2003), 515–575] and Shirai and Takahashi [Random point fields associated with certain Fredholm determinants II: fermion shifts and their ergodic properties. Ann. Probab.31 (2003), 1533–1564]. We prove its continuum version. For this purpose, we also prove the Bernoulli property for the tree representations of the determinantal point processes.
\mathbb{Z}^d
with translation-invariant kernels, the Bernoulli property was proved by Lyons and Steif [Stationary determinantal processes: phase multiplicity, bernoullicity, and domination. Duke Math. J.120 (2003), 515–575] and Shirai and Takahashi [Random point fields associated with certain Fredholm determinants II: fermion shifts and their ergodic properties. Ann. Probab.31 (2003), 1533–1564]. We prove its continuum version. For this purpose, we also prove the Bernoulli property for the tree representations of the determinantal point processes.