Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T14:17:34.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphisms between determinantal point processes with translation-invariant kernels and Poisson point processes

Part of: Ergodic theory Stochastic processes

Published online by Cambridge University Press:  04 December 2020

SHOTA OSADA Open the ORCID record for SHOTA OSADA [Opens in a new window]
SHOTA OSADA*
Affiliation:
Institute of Mathematics for Industry, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
*
e-mail: s-osada@math.kyushu-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the Bernoulli property for determinantal point processes on 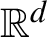$ \mathbb{R}^d $ with translation-invariant kernels. For the determinantal point processes on 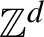$ \mathbb{Z}^d $ with translation-invariant kernels, the Bernoulli property was proved by Lyons and Steif [Stationary determinantal processes: phase multiplicity, bernoullicity, and domination. Duke Math. J.120 (2003), 515–575] and Shirai and Takahashi [Random point fields associated with certain Fredholm determinants II: fermion shifts and their ergodic properties. Ann. Probab.31 (2003), 1533–1564]. We prove its continuum version. For this purpose, we also prove the Bernoulli property for the tree representations of the determinantal point processes.

Keywords

Bernoulli propertydeterminantal point processestree representations

MSC classification

Primary: 37A50: Relations with probability theory and stochastic processes
Secondary: 60G55: Point processes
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3807 - 3820
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Bufetov, A. I. and Shirai, T.. Quasi-symmetries and rigidity for determinantal point processes associated with de Branges spaces. Proc. Japan Acad. Ser. A Math. Sci. 93(1) (2017), 1–5.10.3792/pjaa.93.1CrossRefGoogle Scholar
Kalikow, S. and Weiss, B.. Explicit codes for some infinite entropy Bernoulli shifts. Ann. Probab. 20(1) (1992), 397–402.10.1214/aop/1176989933CrossRefGoogle Scholar
Liggett, T. M.. Interacting Particle Systems (Grundlehren der Mathematischen Wissenschaften, 276). Springer, New York, 1985.Google Scholar
Lyons, R.. Determinantal probability measures. Publ. Math. Inst. Hautes Études Sci. 98 (2003), 167–212.10.1007/s10240-003-0016-0CrossRefGoogle Scholar
Lyons, R. and Steif, J. E.. Stationary determinantal processes: phase multiplicity, bernoullicity, and domination. Duke Math. J. 120 (2003), 515–575.10.1215/S0012-7094-03-12032-3CrossRefGoogle Scholar
Ornstein, D. S.. Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4 (1970), 337–352.10.1016/0001-8708(70)90029-0CrossRefGoogle Scholar
Ornstein, D. S.. Two Bernoulli shifts with infinite entropy are isomorphic. Adv. Math. 5 (1970), 339–348.10.1016/0001-8708(70)90008-3CrossRefGoogle Scholar
Ornstein, D. S.. Ergodic Theory, Randomness, and Dynamical Systems. Yale University Press, New Haven, CT, 1974.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–144.10.1007/BF02790325CrossRefGoogle Scholar
Osada, H. and Osada, S.. Discrete approximations of determinantal point processes on continuous spaces: tree representations and the tail triviality. J. Stat. Phys. 170 (2018), 421–435.10.1007/s10955-017-1928-2CrossRefGoogle Scholar
Shirai, T. and Takahashi, Y.. Random point fields associated with certain Fredholm determinants I: fermion, Poisson and boson processes. J. Funct. Anal. 205 (2003), 414–463.10.1016/S0022-1236(03)00171-XCrossRefGoogle Scholar
Shirai, T. and Takahashi, Y.. Random point fields associated with certain Fredholm determinants II: fermion shifts and their ergodic properties. Ann. Probab. 31 (2003), 1533–1564.10.1214/aop/1055425789CrossRefGoogle Scholar
Soshnikov, A.. Determinantal random point fields. Russian Math. Surveys 55 (2000), 923–975.10.1070/RM2000v055n05ABEH000321CrossRefGoogle Scholar
Steif, J. E.. Space–time bernoullicity of the lower and upper stationary processes for attractive spin systems. Ann. Probab. 19(2) (1991), 609–635.CrossRefGoogle Scholar