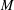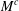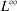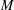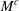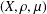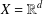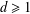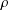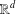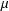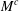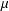1 results
DICHOTOMY PROPERTY FOR MAXIMAL OPERATORS IN A NONDOUBLING SETTING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 454-466
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
-
We investigate a dichotomy property for Hardy–Littlewood maximal operators, noncentred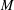
$M$ and centred 
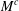$M^{c}$, that was noticed by Bennett et al. [‘Weak-
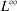$L^{\infty }$ and BMO’, Ann. of Math. (2) 113 (1981), 601–611]. We illustrate the full spectrum of possible cases related to the occurrence or not of this property for 
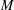$M$ and 
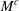$M^{c}$ in the context of nondoubling metric measure spaces 
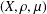$(X,\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707})$. In addition, if 
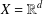$X=\mathbb{R}^{d}$, 
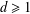$d\geq 1$, and 
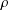$\unicode[STIX]{x1D70C}$ is the metric induced by an arbitrary norm on 
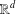$\mathbb{R}^{d}$, then we give the exact characterisation (in terms of 
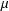$\unicode[STIX]{x1D707}$) of situations in which 
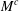$M^{c}$ possesses the dichotomy property provided that 
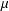$\unicode[STIX]{x1D707}$ satisfies some very mild assumptions.
