Darmon, Lauder, and Rotger conjectured that the relative tangent space of an eigencurve at a classical, ordinary, irregular weight one point is of dimension two. This space can be identified with the space of normalized overconvergent generalized eigenforms, whose Fourier coefficients can be conjecturally described explicitly in terms of 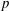 $p$-adic logarithms of algebraic numbers. This article presents the proof of this conjecture in the case where the weight one point is the intersection of two Hida families of Hecke theta series.
$p$-adic logarithms of algebraic numbers. This article presents the proof of this conjecture in the case where the weight one point is the intersection of two Hida families of Hecke theta series.
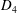 $D_{4}$ Image
$D_{4}$ Image