Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T16:35:36.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Irregular Weight One Points with $D_{4}$ Image

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  04 January 2019

Hao Lee
Hao Lee*
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec Email: hao.lee@mail.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Darmon, Lauder, and Rotger conjectured that the relative tangent space of an eigencurve at a classical, ordinary, irregular weight one point is of dimension two. This space can be identified with the space of normalized overconvergent generalized eigenforms, whose Fourier coefficients can be conjecturally described explicitly in terms of 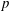$p$-adic logarithms of algebraic numbers. This article presents the proof of this conjecture in the case where the weight one point is the intersection of two Hida families of Hecke theta series.

Keywords

weight one pointsirregulardihedral imagegeneralized eigenformeigencurvetangent space

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11F80: Galois representations
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 109 - 118
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was partially supported by NSERC CGS-Master’s Program.

References

Bellaïche, J. and Dimitrov, M., On the eigencurve at classical weight 1 points . Duke Math. J. 165(2016), no. 2, 245–266. https://doi.org/10.1215/00127094-3165755.Google Scholar
Cho, S. and Vatsal, V., Deformations of induced Galois representations . J. Reine Angew. Math. 556(2003), 78–98. https://doi.org/10.1515/crll.2003.025.Google Scholar
Darmon, H., Lauder, A., and Rotger, V., First order p-adic deformations of weight one newforms. https://mat-web.upc.edu/people/victor.rotger/docs/DLR4.pdf.Google Scholar
Darmon, H., Lauder, A., and Rotger, V., Overconvergent generalised eigenforms of weight one and class fields of real quadratic fields . Adv. Math. 283(2015), 130–142. https://doi.org/10.1016/j.aim.2015.07.007.Google Scholar
Darmon, H., Lauder, A., and Rotger, V., Stark points and p-adic iterated integrals attached to modular forms of weight one . Forum Math. Pi 3(2015), e8. 95 pp. https://doi.org/10.1017/fmp.2015.7.Google Scholar
Darmon, H., Rotger, V., and Zhao, Y., The Birch and Swinnerton-Dyer conjecture for ℚ-curves and Oda’s period relations . In: Geometry and analysis of automorphic forms of several variables, Ser. Number Theory Appl, 7, World Sci. Publ., Hackensack, NJ, 2012, pp. 1–40. https://doi.org/10.1142/9789814355605_0001.Google Scholar
Deligne, P. and Serre, J-P., Formes modulaires de poids 1 . Ann. Sci. Éc. Norm. Sup. (4) 7(1974), 507–530.10.24033/asens.1277Google Scholar
Mazur, B., Deforming Galois representations . In: Galois Groups over ℚ, Math. Sci. Res. Inst. Publ., 16, Springer, New York, 1989, pp. 385–437. https://doi.org/10.1007/978-1-4613-9649-9_7.Google Scholar
Rohrlich, D., Almost abelian Artin representations of $\mathbb{Q}$ . http://math.bu.edu/people/rohrlich/aa.pdf.Google Scholar
Shintani, T., On certain ray class invariants of real quadratic fields . J. Math. Soc. Japan 30(1978), no. 1, 139–167. https://doi.org/10.2969/jmsj/03010139.Google Scholar