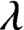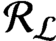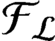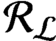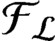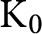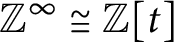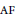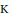We investigate categorical and amalgamation properties of the functor $\operatorname{Id_c}$ assigning to every partially ordered abelian group $G$ its $\langle \vee, 0 \rangle$-semilattice of compact ideals $\operatorname{Id_c} G$. Our main result is the following.
Theorem 1. Every diagram of finite Boolean semilattices indexed by a finite dismantlable partially ordered set can be lifted, with respect to the$\operatorname{Id_c}$functor, by a diagram of pseudo-simplicial vector spaces.
Pseudo-simplicial vector spaces are a special kind of finite-dimensional partially ordered vector spaces with interpolation over the field of rational numbers. The methods introduced also make it possible to prove the following ring-theoretical result.
Theorem 2. For any countable distributive$\langle \vee, 0 \rangle$-semilattices$S$and$T$and any field$K$, any$\langle \vee, 0 \rangle$-homomorphism$f \colon S \to T$can be lifted, with respect to the$\operatorname{Id_c}$functor on rings, by a homomorphism $f \colon A \to B$of$K$-algebras, for countably dimensional locally matricial algebras$A$and$B$over$K$.
We also state a lattice-theoretical analogue of Theorem 2 (with respect to the $\operatorname{Con_c}$ functor), and we provide counterexamples to various related statements. In particular, we prove that the result of Theorem 1 cannot be achieved with simplicial vector spaces alone.
 $\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
$\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS


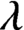

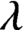
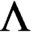
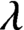
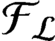
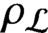
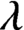
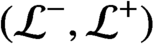

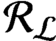
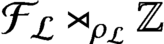 . It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If
. It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If