Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T05:43:35.623Z Has data issue: false hasContentIssue false
  • English
  • Français

The Category of Bratteli Diagrams

Published online by Cambridge University Press:  20 November 2018

Massoud Amini ,
George A. Elliott  and
Nasser Golestani
Massoud Amini
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran, Iran. e-mail: mamini@modares.ac.ir, n.golestani@modares.ac.ir
George A. Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 2E4. e-mail: elliott@math.toronto.edu
Nasser Golestani
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran, Iran. e-mail: mamini@modares.ac.ir, n.golestani@modares.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A category structure for Bratteli diagrams is proposed and a functor from the category of 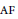$\text{AF}$ algebras to the category of Bratteli diagrams is constructed. Since isomorphism of Bratteli diagrams in this category coincides with Bratteli’s notion of equivalence, we obtain in particular a functorial formulation of Bratteli’s classification of 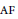$\text{AF}$ algebras (and at the same time, of Glimm’s classification of $\text{UHF}$ algebras). It is shown that the three approaches to classification of 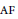$\text{AF}$ algebras, namely, through Bratteli diagrams, 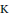$\text{K}$-theory, and a certain natural abstract classifying category, are essentially the same from a categorical point of view.

Keywords

46L0546L3546M15C*-algebracategoryfunctorAF algebradimension groupBratteli diagram
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 5 , 01 October 2015 , pp. 990 - 1023
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Blackadar, B., K-Theory for Operator Algebras. Mathematical Sciences Research Institute Publications, Cambridge University Press, 1998.Google Scholar
[2] Bratteli, O., Inductive limits of finite-dimensional C* -algebras. Trans. Amer. Math. Soc. 171(1972),195–234.Google Scholar
[3] Chuaqui, R., Axiomatic Set Theory: Impredicative Theories of Classes. North-Holland Mathematics Studies, Volume 51, Elsevier, Amsterdam, 1981.Google Scholar
[4] Davidson, K. R., C* -Algebras by Example. Fields Institute Monographs 6, American Mathematical Society, Providence, 1996.Google Scholar
[5] Dixmier, J., On some C* -algebras considered by Glimm. J. Functional Analysis 1(1967), 182–203.http://dx.doi.Org/10.1016/0022-1236(67)90031-6 Google Scholar
[6] Durand, F., Host, B., and Skau, C., Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergodic Theory Dynam. Systems 19(1999), 953–993.http://dx.doi.Org/10.1017/S0143385799133947 Google Scholar
[7] Effros, E. G., Handelman, D. E., and Shen, C. L., Dimension groups and their affine transformations. Amer. J. Math. 102(1980), 385–402.http://dx.doi.Org/10.2307/2374244 Google Scholar
[8] Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 38(1976), 29–44.http://dx.doi.Org/10.1016/0021-8693(76)90242-8 Google Scholar
[9] Elliott, G. A., On the classification of C* -algebras of real rank zero. J. Reine Angew. Math. 443(1993), 179–219.Google Scholar
[10] Elliott, G. A., Towards a theory of classification. Adv. Math. 223(2010), 30–48. http://dx.doi.Org/10.1016/j.aim.2009.07.018 Google Scholar
[11] Glimm, J. G., On a certain class of operator algebras. Trans. Amer. Math. Soc. 95(1960), 318–340.http://dx.doi.Org/10.1090/S0002-9947-1960-0112057-5 Google Scholar
[12] Goldblatt, R., Topoi, the Categorical Analysis of Logic. Elsevier Science Publishers, New York, 1984.Google Scholar
[13] Lazar, A. J. and Taylor, D. C., Approximately finite-dimensional C* -algebras and Bratteli diagrams. Trans. Amer. Math. Soc. 259(1980), 599–619.Google Scholar
[14] Ren, L. B., Introduction to Operator Algebras. World Scientific, Singapore, 1992.Google Scholar
[15] Mac Lane, S., Categories for the Working Mathematician. Second edition, Springer, New York, 1998.Google Scholar
[16] Murphy, G., C*-Algebras and Operator Theory. Academic Press, New York, 1990.Google Scholar
[17] Takesaki, M., Theory of Operator Algebras Vol I., Springer, New York, 1979.Google Scholar
[18] Wegge-Olsen, N. E., K-Theory and C* -Algebras, A Friendly Approach. The Clarendon Press, New York, 1993.Google Scholar