We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A pointwise estimate for the rate of approximation by polynomials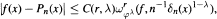 
, For 0 ≤ ƛ ≤ 1, integer r, 
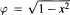and δn(x) = n-1 + φ(x), is achieved here. This formula bridges the gap between the classical estimate mentioned in most texts on approximation and obtained by Timan and others (ƛ = 0) and the recently developed estimate by Totik and first author (ƛ = 1 ). Furthermore, a matching converse result and estimates on derivatives of the approximating polynomials and their rate of approximation are derived. These results also cover the range between the classical pointwise results and the modern norm estimates for C[— 1,1].
