Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:59:42.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation of Functions by Polynomials in C[-L, 1]

Published online by Cambridge University Press:  20 November 2018

Z. Ditzian  and
D. Jiang
Z. Ditzian
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta
D. Jiang
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

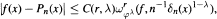A pointwise estimate for the rate of approximation by polynomials , For 0 ≤ ƛ ≤ 1, integer r, 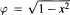and δn(x) = n-1 + φ(x), is achieved here. This formula bridges the gap between the classical estimate mentioned in most texts on approximation and obtained by Timan and others (ƛ = 0) and the recently developed estimate by Totik and first author (ƛ = 1 ). Furthermore, a matching converse result and estimates on derivatives of the approximating polynomials and their rate of approximation are derived. These results also cover the range between the classical pointwise results and the modern norm estimates for C[— 1,1].

Keywords

41A2541A27Polynomial approximationdirect and converse results
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 5 , 01 October 1992 , pp. 924 - 940
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. DeVore, R., Lp[—1,1] approximation by algebraic polynomials, linear spaces and approximation, (ed. R Butzer, L. and Nagy, B.Sz), Birkhauser Verlag, Basel, 1978, 397–406.Google Scholar
2. Ditzian, Z., On interpolation ofLp[a, b] and weighted Sobolev spaces, Pacific J. Math. 90(1980), 307–323.Google Scholar
3. Ditzian, Z., Interpolation theorems on the rate of convergence of Bernstein polynomials, Approximation Theory III, (ed. Cheney, E.W.), Academic Press, 1980, 341–347.Google Scholar
4. Ditzian, Z. and Totik, V., Moduli of Smoothness, Springer-Verlag, 1987.Google Scholar
5. Lorentz, G.G., Approximation of Functions, Holt, Rinehart and Winston, 1966, reprinted by Chelsea, 1988.Google Scholar
6. Motornii, V.P., Approximation of functions by algebraic polynomials in Lp metric (Russian), Izv. Akad. Nauk. SSSR, 35(1971), 874–899.Google Scholar
7. Timan, A.F., Theory of functions of a real variable, English translation 1963, Pergamon Press, The MacMillan Co., Russian original published in Moscow by Fizmatgiz in 1960.Google Scholar