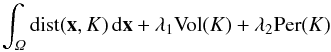Search

Summary

We give some important applications of the Hahn-Banach Theorem. We prove the existence of a support functional and hence that X^* separates points in X. Then we prove the existence of a functional that encodes the distance from a linear subspace, which is an important ingredient in a number of subsequent proofs. We show that separability of X^* implies separability of X, define the Banach adjoint of a linear map (between Banach spaces), and prove the existence of ‘generalised Banach limits’.

In this paper we study the compact and convex setsK ⊆ Ω ⊆ ℝ2 that minimize

\begin{equation*} \int_{\Omega} \dist(\x,K) \,{\rm d}\x +\lambda_1 {\rm Vol}(K)+\lambda_2 {\rm Per}(K) \end{equation*}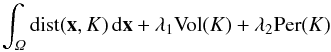

\int_{Ω} dist (x,K) d x + λ_{1} Vol (K) + λ_{2} Per (K)

for some constants λ1 andλ2, that could possibly be zero. We compute in particularthe second order derivative of the functional and use it to exclude smooth points ofpositive curvature for the problem with volume constraint. The problem with perimeterconstraint behaves differently since polygons are never minimizers. Finally using a purelygeometrical argument from Tilli [J. Convex Anal. 17 (2010)583–595] we can prove that any arbitrary convex set can be a minimizer when both perimeterand volume constraints are considered.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

20 - Some Applications of the Hahn–Banach Theorem

Summary

On convex sets that minimize the averagedistance

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

20 - Some Applications of the Hahn–Banach Theorem

Summary

On convex sets that minimize the averagedistance