We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A suitable notion of weak amenability for dual Banach algebras, which we call weak Connes amenability, is defined and studied. Among other things, it is proved that the measure algebra M(G) of a locally compact group G is always weakly Connes amenable. It can be a complement to Johnson’s theorem that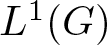 
$L^1(G)$ is always weakly amenable [10].
