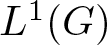1. Introduction
Amenable Banach algebras were introduced by Johnson in [Reference Johnson12]. There are several variants of amenability, two of the most notable are weak amenability and Connes amenability. The concept of weak amenability for Banach algebras was introduced by Johnson in [Reference Johnson and Pier11], and it generalizes that introduced by Bade, Curtis and Dales for commutative Banach algebras in [Reference Bade, Curtis and Dales1]. The notion of Connes amenability was systematically introduced by Runde in [Reference Runde15]; however, it had been considered previously under different names. We recall the definitions in Definitions 2.1 and 2.2 below.
The purpose of this paper is to study a new notion of weak amenability for dual Banach algebras, which will play the role that weak amenability does for usual Banach algebras. Similar to Connes amenability, this new variant of amenability takes the dual space structure of a dual Banach algebra into account.
One of the most important dual Banach algebras is the measure algebra M(G) of a locally compact group G. Weak amenability in the sense of [Reference Johnson and Pier11] is too strong to deal with M(G) in a satisfactory manner. In [Reference Dales, Ghahramani and Helemskii3], Dales, Ghahramani and Helemskii prove that M(G) is weakly amenable if and only if G is discrete. In contrast, weak Connes amenability of M(G), in the sense of Definition 3.2 below, is not a restrictive demand.
The organization of the paper is as follows. In § 2, we recall some background notations and definitions.
In § 3, weak Connes amenability for dual Banach algebras is introduced. It is shown that the corresponding class of such algebras includes all Connes amenable dual Banach algebras (Theorem 3.5), as well as all weakly amenable dual Banach algebras (Theorem 3.6). For a locally compact group G, the measure algebra M(G) is weakly Connes amenable (Theorem 3.7).
In § 4, some basic and hereditary properties are given. We study weak Connes amenability of direct sums of dual Banach algebras (Theorem 4.3). Weak Connes amenability of the enveloping dual Banach algebras is also discussed (Corollary 4.5).
In § 5, we verify this new notion for some certain algebras. Examples are given to distinguish between the new notion and the classical concepts of amenability. In particular, we present a class of weakly Connes amenable dual Banach algebras which are neither Connes amenable nor weakly amenable (Theorem 5.5).
2. Preliminaries
Suppose that ![]() $\mathfrak{A}$ is a Banach algebra. It is known that the projective tensor product
$\mathfrak{A}$ is a Banach algebra. It is known that the projective tensor product ![]() $\mathfrak{A} \hat{\otimes} \mathfrak{A}$ is a Banach
$\mathfrak{A} \hat{\otimes} \mathfrak{A}$ is a Banach ![]() $\mathfrak{A}$-bimodule in the canonical way. There is a continuous linear
$\mathfrak{A}$-bimodule in the canonical way. There is a continuous linear ![]() $\mathfrak{A}$-bimodule homomorphism
$\mathfrak{A}$-bimodule homomorphism ![]() $\pi:\mathfrak A\widehat\otimes\mathfrak A\longrightarrow\mathfrak A$ such that
$\pi:\mathfrak A\widehat\otimes\mathfrak A\longrightarrow\mathfrak A$ such that ![]() $
\pi ( a \otimes b) = ab$ for
$
\pi ( a \otimes b) = ab$ for ![]() $a,b \in \mathfrak{A}$. If E is a Banach
$a,b \in \mathfrak{A}$. If E is a Banach ![]() $\mathfrak{A}$-bimodule, then so is the dual space
$\mathfrak{A}$-bimodule, then so is the dual space ![]() $E^*$. A continuous linear map
$E^*$. A continuous linear map ![]() $D:\mathfrak{A} \longrightarrow E$ is a derivation if it satisfies
$D:\mathfrak{A} \longrightarrow E$ is a derivation if it satisfies ![]() $ D(ab) = D(a) \ . \ b + a \ . \ D(b) $ for all
$ D(ab) = D(a) \ . \ b + a \ . \ D(b) $ for all ![]() $a,b \in
\mathfrak{A}$. We call D inner if there is
$a,b \in
\mathfrak{A}$. We call D inner if there is ![]() $x \in
E$ such that
$x \in
E$ such that ![]() $ D(a) = ad_x(a) := a \ . \ x - x \ . \ a$ for every
$ D(a) = ad_x(a) := a \ . \ x - x \ . \ a$ for every ![]() $a \in
\mathfrak{A}$.
$a \in
\mathfrak{A}$.
Definition 2.1. A Banach algebra ![]() $\mathfrak{A}$ is weakly amenable if every derivation
$\mathfrak{A}$ is weakly amenable if every derivation ![]() $D: \mathfrak{A} \longrightarrow
\mathfrak{A}^*$ is inner.
$D: \mathfrak{A} \longrightarrow
\mathfrak{A}^*$ is inner.
Let X be a Banach space. We simply denote by wk and ![]() $w^*$, the
$w^*$, the ![]() $\sigma( X, X^*)$-topology and the
$\sigma( X, X^*)$-topology and the ![]() $\sigma( X^*, X)$-topology on X and
$\sigma( X^*, X)$-topology on X and ![]() $X^*$, respectively.
$X^*$, respectively.
Let ![]() $\mathfrak{A}$ be a Banach algebra. A Banach
$\mathfrak{A}$ be a Banach algebra. A Banach ![]() $\mathfrak{A}$-bimodule E is dual if there is a closed submodule
$\mathfrak{A}$-bimodule E is dual if there is a closed submodule ![]() $E_*$ of
$E_*$ of ![]() $E^*$ such that
$E^*$ such that ![]() $E = (E_*)^*$. We call
$E = (E_*)^*$. We call ![]() $E_*$ the predual of E. A Banach algebra
$E_*$ the predual of E. A Banach algebra ![]() $\mathfrak{A}=(\mathfrak{A}_*) ^*$ is dual if it is dual as a Banach
$\mathfrak{A}=(\mathfrak{A}_*) ^*$ is dual if it is dual as a Banach ![]() $\mathfrak{A}$-bimodule. Equivalently, a Banach algebra
$\mathfrak{A}$-bimodule. Equivalently, a Banach algebra ![]() $\mathfrak{A}$ is dual if it is a dual Banach space such that its multiplication is separately continuous in the
$\mathfrak{A}$ is dual if it is a dual Banach space such that its multiplication is separately continuous in the ![]() $w^*$-topology.
$w^*$-topology.
Let ![]() $\mathfrak{A}$ be a dual Banach algebra, and let E be a dual Banach
$\mathfrak{A}$ be a dual Banach algebra, and let E be a dual Banach ![]() $\mathfrak{A}$-bimodule. Then, we say that E is normal if the module actions of
$\mathfrak{A}$-bimodule. Then, we say that E is normal if the module actions of ![]() $\mathfrak{A}$ on E are
$\mathfrak{A}$ on E are ![]() $w^*$–
$w^*$–![]() $w^*$ continuous.
$w^*$ continuous.
Definition 2.2. A dual Banach algebra ![]() $\mathfrak{A}$ is Connes amenable if for every normal, dual Banach
$\mathfrak{A}$ is Connes amenable if for every normal, dual Banach ![]() $\mathfrak{A}$-bimodule E, every
$\mathfrak{A}$-bimodule E, every ![]() $w^*$–
$w^*$–![]() $w^*$ continuous derivation
$w^*$ continuous derivation ![]() $D : \mathfrak{A} \longrightarrow
E$ is inner.
$D : \mathfrak{A} \longrightarrow
E$ is inner.
Let ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra and let E be a Banach
$\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra and let E be a Banach ![]() $\mathfrak{A}$-bimodule. We write
$\mathfrak{A}$-bimodule. We write ![]() $\sigma wc(E)$ for the set of all elements
$\sigma wc(E)$ for the set of all elements ![]() $ x \in E$ such that the maps
$ x \in E$ such that the maps
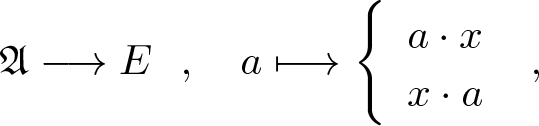 \begin{equation*} \mathfrak{A} \longrightarrow E \ \ , \ \ \ a
\longmapsto \left \{
\begin{array}{ll}
a \cdot x \\
x \cdot a
\end{array} \right. \ , \end{equation*}
\begin{equation*} \mathfrak{A} \longrightarrow E \ \ , \ \ \ a
\longmapsto \left \{
\begin{array}{ll}
a \cdot x \\
x \cdot a
\end{array} \right. \ , \end{equation*} are ![]() $w^*$–wk continuous. It is well known that
$w^*$–wk continuous. It is well known that ![]() $\sigma wc(E)$ is a closed submodule of E, and
$\sigma wc(E)$ is a closed submodule of E, and ![]() $\sigma wc(E)^*$ is always normal. It is shown in [Reference Runde16, Corollary 4.6] that
$\sigma wc(E)^*$ is always normal. It is shown in [Reference Runde16, Corollary 4.6] that ![]() $
\pi^*(\mathfrak{A}_*) \subseteq \sigma wc(\mathfrak{A} \hat{\otimes}
\mathfrak{A} )^*$. Taking adjoints, we can extend π to an
$
\pi^*(\mathfrak{A}_*) \subseteq \sigma wc(\mathfrak{A} \hat{\otimes}
\mathfrak{A} )^*$. Taking adjoints, we can extend π to an ![]() $\mathfrak{A}$-bimodule homomorphism
$\mathfrak{A}$-bimodule homomorphism ![]() $\pi_{\sigma wc}$ from
$\pi_{\sigma wc}$ from ![]() $ \sigma
wc((\mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$ to
$ \sigma
wc((\mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$ to ![]() $\mathfrak{A}$. A
$\mathfrak{A}$. A ![]() $\sigma wc$-virtual diagonal for a dual Banach algebra
$\sigma wc$-virtual diagonal for a dual Banach algebra ![]() $\mathfrak{A}$ is an element
$\mathfrak{A}$ is an element ![]() $M \in \sigma
wc((\mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$ such that
$M \in \sigma
wc((\mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$ such that ![]() $ a \cdot M = M \cdot a$ and
$ a \cdot M = M \cdot a$ and ![]() $ a \pi_{\sigma wc} (M) = a$ for
$ a \pi_{\sigma wc} (M) = a$ for ![]() $a \in
\mathfrak{A}$. It is known that Connes amenability of
$a \in
\mathfrak{A}$. It is known that Connes amenability of ![]() $\mathfrak{A}$ is equivalent to existence of a
$\mathfrak{A}$ is equivalent to existence of a ![]() $\sigma wc$-virtual diagonal for
$\sigma wc$-virtual diagonal for ![]() $\mathfrak{A}$ [Reference Runde16].
$\mathfrak{A}$ [Reference Runde16].
Our comprehensive references on amenability of Banach algebras are [Reference Dales2, Reference Runde17].
3. Weak Connes amenability
Let ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra, and let E be a Banach
$\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra, and let E be a Banach ![]() $\mathfrak{A}$-bimodule. We denote by
$\mathfrak{A}$-bimodule. We denote by ![]() $j_E : E^* \longrightarrow
\sigma wc (E)^* $ the adjoint of the inclusion map
$j_E : E^* \longrightarrow
\sigma wc (E)^* $ the adjoint of the inclusion map ![]() $ \sigma wc (E) \hookrightarrow E$. It is clear that jE is an
$ \sigma wc (E) \hookrightarrow E$. It is clear that jE is an ![]() $\mathfrak{A}$-bimodule homomorphism and
$\mathfrak{A}$-bimodule homomorphism and ![]() $ \langle x , j_E (f) \rangle =
f (x)$ for all
$ \langle x , j_E (f) \rangle =
f (x)$ for all ![]() $x \in \sigma wc (E)$ and
$x \in \sigma wc (E)$ and ![]() $ f \in E^*$.
$ f \in E^*$.
We start with the following observation.
Lemma 3.1. Let ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra, let E be a Banach
$\mathfrak{A} = (\mathfrak{A}_*)^*$ be a dual Banach algebra, let E be a Banach ![]() $\mathfrak{A}$-bimodule, and let
$\mathfrak{A}$-bimodule, and let ![]() $D :\mathfrak{A} \longrightarrow E^*$ be a derivation. Then:
$D :\mathfrak{A} \longrightarrow E^*$ be a derivation. Then:
(i) The map ![]() $j_{E} \circ D : \mathfrak{A} \longrightarrow \sigma wc (E )^*$ is a derivation;
$j_{E} \circ D : \mathfrak{A} \longrightarrow \sigma wc (E )^*$ is a derivation;
(ii) If D is inner, then so is ![]() $j_{E} \circ D$. Furthermore,
$j_{E} \circ D$. Furthermore, ![]() $j_{E} \circ ad_f = ad_{j_{E}(f)}$ for each
$j_{E} \circ ad_f = ad_{j_{E}(f)}$ for each ![]() $f \in E^*$;
$f \in E^*$;
(iii) For every ![]() $f \in E^*$,
$f \in E^*$, ![]() $j_{E} \circ ad_f : \mathfrak{A} \longrightarrow \sigma wc (E )^*$ is
$j_{E} \circ ad_f : \mathfrak{A} \longrightarrow \sigma wc (E )^*$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous.
$w^*$ continuous.
Proof. (i) For every ![]() $a, b \in \mathfrak{A} $ and
$a, b \in \mathfrak{A} $ and ![]() $ x \in \sigma wc (E )$ we have
$ x \in \sigma wc (E )$ we have
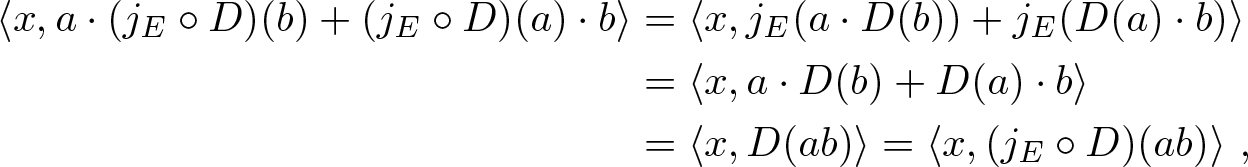 \begin{align*}
\langle x , a \cdot (j_{E} \circ D ) (b) + (j_{E} \circ D ) (a) \cdot b \rangle &= \langle x , j_{E}( a \cdot D (b) ) +
j_{E} ( D (a) \cdot b ) \rangle \\ &= \langle x , a \cdot D (b) + D (a) \cdot b \rangle \\ &= \langle x , D (a b) \rangle =
\langle x , ( j_{E} \circ D ) (a b) \rangle \ ,
\end{align*}
\begin{align*}
\langle x , a \cdot (j_{E} \circ D ) (b) + (j_{E} \circ D ) (a) \cdot b \rangle &= \langle x , j_{E}( a \cdot D (b) ) +
j_{E} ( D (a) \cdot b ) \rangle \\ &= \langle x , a \cdot D (b) + D (a) \cdot b \rangle \\ &= \langle x , D (a b) \rangle =
\langle x , ( j_{E} \circ D ) (a b) \rangle \ ,
\end{align*} and hence ![]() $j_{E} \circ D$ is a derivation.
$j_{E} \circ D$ is a derivation.
(ii) This is a simple calculation.
(iii) It follows from (ii) and normality of ![]() $ \sigma wc (E )^* $.
$ \sigma wc (E )^* $.
Definition 3.2. A dual Banach algebra ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ is weakly Connes amenable if for every derivation
$\mathfrak{A} = (\mathfrak{A}_*)^*$ is weakly Connes amenable if for every derivation ![]() $D
:\mathfrak{A} \longrightarrow \mathfrak{A}^*$ such that
$D
:\mathfrak{A} \longrightarrow \mathfrak{A}^*$ such that ![]() $j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is
$j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous, derivation
$w^*$ continuous, derivation ![]() $j_{\mathfrak{A}} \circ D$ is inner.
$j_{\mathfrak{A}} \circ D$ is inner.
Remark 3.3. For a dual Banach algebra ![]() $\mathfrak{A} $,
$\mathfrak{A} $, ![]() $\sigma wc (\mathfrak{A} )$ is a closed (two-sided) ideal of
$\sigma wc (\mathfrak{A} )$ is a closed (two-sided) ideal of ![]() $\mathfrak{A} $. To see this, take
$\mathfrak{A} $. To see this, take ![]() $a \in \sigma wc (\mathfrak{A} )$,
$a \in \sigma wc (\mathfrak{A} )$, ![]() $b \in \mathfrak{A} $, and let
$b \in \mathfrak{A} $, and let  $ c_\alpha \stackrel{w^*} \longrightarrow c $ in
$ c_\alpha \stackrel{w^*} \longrightarrow c $ in ![]() $\mathfrak{A} $. Because
$\mathfrak{A} $. Because  $c_\alpha a \stackrel{wk} \longrightarrow c a $, for every
$c_\alpha a \stackrel{wk} \longrightarrow c a $, for every ![]() $\varphi \in \mathfrak{A}^*$, we have
$\varphi \in \mathfrak{A}^*$, we have
so that ![]() $ a b \in \sigma wc (\mathfrak{A} )$. Next, by
$ a b \in \sigma wc (\mathfrak{A} )$. Next, by ![]() $w^*$-continuity of the multiplication,
$w^*$-continuity of the multiplication,  $ c_\alpha b \stackrel{w^*} \longrightarrow c b$. Then,
$ c_\alpha b \stackrel{w^*} \longrightarrow c b$. Then,  $c_\alpha ( b a) = (c_\alpha b ) a \stackrel{wk} \longrightarrow ( c b ) a = c ( b a)$, which means
$c_\alpha ( b a) = (c_\alpha b ) a \stackrel{wk} \longrightarrow ( c b ) a = c ( b a)$, which means ![]() $ b a \in \sigma wc (\mathfrak{A} )$.
$ b a \in \sigma wc (\mathfrak{A} )$.
For a given dual Banach algebra ![]() $\mathfrak{A} $, it would be interesting to determine the set
$\mathfrak{A} $, it would be interesting to determine the set ![]() $\sigma wc (\mathfrak{A} )$. However, special care should be taken with the trivial cases
$\sigma wc (\mathfrak{A} )$. However, special care should be taken with the trivial cases ![]() $\sigma wc (\mathfrak{A} ) = \{0 \}$ and
$\sigma wc (\mathfrak{A} ) = \{0 \}$ and ![]() $\sigma wc (\mathfrak{A} ) = \mathfrak{A}$, as follows.
$\sigma wc (\mathfrak{A} ) = \mathfrak{A}$, as follows.
Remark 3.4. Let ![]() $\mathfrak{A}$ be a dual Banach algebra. Then:
$\mathfrak{A}$ be a dual Banach algebra. Then:
(i) If
 $\sigma wc (\mathfrak{A} ) = \{0 \}$, then
$\sigma wc (\mathfrak{A} ) = \{0 \}$, then  $j_{\mathfrak{A}} $ is the zero map. Therefore, for every derivation
$j_{\mathfrak{A}} $ is the zero map. Therefore, for every derivation  $D
:\mathfrak{A} \longrightarrow \mathfrak{A}^*$,
$D
:\mathfrak{A} \longrightarrow \mathfrak{A}^*$,  $j_{\mathfrak{A}} \circ D = 0$. So,
$j_{\mathfrak{A}} \circ D = 0$. So,  $\mathfrak{A} $ is weakly Connes amenable.
$\mathfrak{A} $ is weakly Connes amenable.(ii) If
 $\sigma wc (\mathfrak{A} ) = \mathfrak{A}$ (or equivalently
$\sigma wc (\mathfrak{A} ) = \mathfrak{A}$ (or equivalently  $\mathfrak{A}^*$ is normal by [Reference Runde16, Proposition 4.4]), then
$\mathfrak{A}^*$ is normal by [Reference Runde16, Proposition 4.4]), then  $j_{\mathfrak{A}} $ is the identity map on
$j_{\mathfrak{A}} $ is the identity map on  $ \mathfrak{A}^*$ and then
$ \mathfrak{A}^*$ and then  $j_{\mathfrak{A}} \circ D = D$. In particular, Definition 3.2 becomes:
$j_{\mathfrak{A}} \circ D = D$. In particular, Definition 3.2 becomes:  $\mathfrak{A} $ is weakly Connes amenable if and only if every
$\mathfrak{A} $ is weakly Connes amenable if and only if every  $w^*$-
$w^*$- $w^*$ continuous derivation
$w^*$ continuous derivation  $D : \mathfrak{A} \longrightarrow \mathfrak{A}^*$ is inner.
$D : \mathfrak{A} \longrightarrow \mathfrak{A}^*$ is inner.
As the name suggests, weak Connes amenability is weaker than Connes amenability.
Theorem 3.5. Every Connes amenable dual Banach algebra is weakly Connes amenable.
Proof. Let ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ be a Connes amenable dual Banach algebra, and let
$\mathfrak{A} = (\mathfrak{A}_*)^*$ be a Connes amenable dual Banach algebra, and let ![]() $D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that
$D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that ![]() $j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is
$j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. By the assumption,
$w^*$ continuous. By the assumption, ![]() $j_{\mathfrak{A}} \circ D$ is inner, as required.
$j_{\mathfrak{A}} \circ D$ is inner, as required.
For dual Banach algebras, weak amenability implies weak Connes amenability as follows.
Theorem 3.6. Every weakly amenable dual Banach algebra is weakly Connes amenable.
Proof. Let ![]() $\mathfrak{A} = (\mathfrak{A}_*)^*$ be a weakly amenable dual Banach algebra, and let
$\mathfrak{A} = (\mathfrak{A}_*)^*$ be a weakly amenable dual Banach algebra, and let ![]() $D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that
$D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that ![]() $j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is
$j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. By the assumption, D is inner. Then, by Lemma 3.1(ii),
$w^*$ continuous. By the assumption, D is inner. Then, by Lemma 3.1(ii), ![]() $j_{\mathfrak{A}} \circ D$ is inner.
$j_{\mathfrak{A}} \circ D$ is inner.
It is well known that the measure algebra M(G) of a locally compact group G is a dual Banach algebra with predual ![]() $C_0(G)$.
$C_0(G)$.
Theorem 3.7. Let G be a locally compact group. Then, M(G) is weakly Connes amenable.
Proof. Let ![]() $D : M(G) \longrightarrow M(G)^*$ be a inner derivation such that
$D : M(G) \longrightarrow M(G)^*$ be a inner derivation such that ![]() $j_{M(G)} \circ D : M(G) \longrightarrow \sigma wc ( M(G) )^* $ is
$j_{M(G)} \circ D : M(G) \longrightarrow \sigma wc ( M(G) )^* $ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. By the remark on the final page of [Reference Despic and Ghahramani7], there exists
$w^*$ continuous. By the remark on the final page of [Reference Despic and Ghahramani7], there exists ![]() $ \varphi \in M(G)^*$ for which
$ \varphi \in M(G)^*$ for which ![]() $ D(\delta_g) =ad_\varphi(\delta_g)$ for every
$ D(\delta_g) =ad_\varphi(\delta_g)$ for every ![]() $g \in G$, where δg is the point mass at g. Then,
$g \in G$, where δg is the point mass at g. Then, ![]() $ j_{M(G)} \circ D (\delta_g) =ad_{j(\varphi)}(\delta_g)$ for each
$ j_{M(G)} \circ D (\delta_g) =ad_{j(\varphi)}(\delta_g)$ for each ![]() $g \in G $, by Lemma 3.1 (ii). As
$g \in G $, by Lemma 3.1 (ii). As ![]() $j_{M(G)} \circ D$ is
$j_{M(G)} \circ D$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous and point masses are
$w^*$ continuous and point masses are ![]() $w^*$-dense in M(G), we conclude that
$w^*$-dense in M(G), we conclude that ![]() $j_{M(G)} \circ D =ad_{j(\varphi)} $.
$j_{M(G)} \circ D =ad_{j(\varphi)} $.
We shall require the following, pointed out by the referee.
Remark 3.8. Let ![]() $\mathfrak{A}$ be a finite-dimensional Banach algebra. It is known that
$\mathfrak{A}$ be a finite-dimensional Banach algebra. It is known that ![]() $ \sigma wc (\mathfrak{A})= \mathfrak{A}$, and all norm-continuous derivations are automatically
$ \sigma wc (\mathfrak{A})= \mathfrak{A}$, and all norm-continuous derivations are automatically ![]() $w^*$–
$w^*$–![]() $w^*$ continuous. Hence, for finite-dimensional algebras, weak Connes amenability is equivalent to weak amenability.
$w^*$ continuous. Hence, for finite-dimensional algebras, weak Connes amenability is equivalent to weak amenability.
To end the current section, we wish to include an example of a dual Banach algebra which is not weakly Connes amenable. Indeed, Remark 3.8 is one way to find such examples: It suffices to give an example of a finite-dimensional Banach algebra, which is not weakly amenable.
Example 3.9. (Suggested by the referee) Let ![]() $\mathfrak{A}$ be the
$\mathfrak{A}$ be the ![]() $\mathbb{C}$-algebra generated by an identity element e and a non-zero, square-zero element a. Define a linear map
$\mathbb{C}$-algebra generated by an identity element e and a non-zero, square-zero element a. Define a linear map ![]() $D: \mathfrak{A} \longrightarrow
\mathfrak{A}^*$ by
$D: \mathfrak{A} \longrightarrow
\mathfrak{A}^*$ by
Then, a direct calculation shows that D is a non-zero derivation from ![]() $\mathfrak{A}$ into
$\mathfrak{A}$ into ![]() $\mathfrak{A}^*$. Since
$\mathfrak{A}^*$. Since ![]() $\mathfrak{A}$ is commutative, D is a non-inner derivation. Thus,
$\mathfrak{A}$ is commutative, D is a non-inner derivation. Thus, ![]() $\mathfrak{A}$ is not weakly Connes amenable by Remark 3.8.
$\mathfrak{A}$ is not weakly Connes amenable by Remark 3.8.
4. Hereditary properties and relations
Suppose that ![]() $\mathfrak{A}$ is a Banach algebra and that E is a Banach
$\mathfrak{A}$ is a Banach algebra and that E is a Banach ![]() $\mathfrak{A}$-bimodule. A derivation
$\mathfrak{A}$-bimodule. A derivation ![]() $D:\mathfrak{A} \longrightarrow E^*$ is
$D:\mathfrak{A} \longrightarrow E^*$ is ![]() $w^*$-approximately inner if there exists a net
$w^*$-approximately inner if there exists a net ![]() $(f_\alpha)_\alpha \subseteq E^*$ such that
$(f_\alpha)_\alpha \subseteq E^*$ such that ![]() $ D (a) =w^*-\lim_\alpha ad_{f_\alpha} ( a )$ for all
$ D (a) =w^*-\lim_\alpha ad_{f_\alpha} ( a )$ for all ![]() $a \in
\mathfrak{A}$ [Reference Ghahramani and Loy8]. The concept of
$a \in
\mathfrak{A}$ [Reference Ghahramani and Loy8]. The concept of ![]() $w^*$-approximate Connes amenability was introduced in [Reference Mahmoodi14]. A dual Banach algebra
$w^*$-approximate Connes amenability was introduced in [Reference Mahmoodi14]. A dual Banach algebra ![]() $\mathfrak{A}$ is
$\mathfrak{A}$ is ![]() $w^*$-approximately Connes amenable if for every normal, dual Banach
$w^*$-approximately Connes amenable if for every normal, dual Banach ![]() $\mathfrak{A}$-bimodule E, every
$\mathfrak{A}$-bimodule E, every ![]() $w^*$–
$w^*$–![]() $w^*$ continuous derivation
$w^*$ continuous derivation ![]() $D : \mathfrak{A} \longrightarrow
E$ is
$D : \mathfrak{A} \longrightarrow
E$ is ![]() $w^*$-approximately inner.
$w^*$-approximately inner.
Proposition 4.1. Every commutative, ![]() $w^*$-approximately Connes amenable dual Banach algebra is weakly Connes amenable.
$w^*$-approximately Connes amenable dual Banach algebra is weakly Connes amenable.
Proof. Let ![]() $\mathfrak{A}$ be a commutative,
$\mathfrak{A}$ be a commutative, ![]() $w^*$-approximately Connes amenable dual Banach algebra, and let
$w^*$-approximately Connes amenable dual Banach algebra, and let ![]() $D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that
$D :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ be a derivation such that ![]() $j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is
$j_{\mathfrak{A}} \circ D : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is ![]() $w^*$–
$w^*$–![]() $w^*$ continuous. It follows from
$w^*$ continuous. It follows from ![]() $w^*$-approximate Connes amenability of
$w^*$-approximate Connes amenability of ![]() $\mathfrak{A}$ that
$\mathfrak{A}$ that ![]() $j_{\mathfrak{A}} \circ D = w^*-\lim_\alpha ad_{f_\alpha}$ for some net
$j_{\mathfrak{A}} \circ D = w^*-\lim_\alpha ad_{f_\alpha}$ for some net ![]() $(f_\alpha)_\alpha \subseteq \sigma wc (\mathfrak{A} )^*$. As
$(f_\alpha)_\alpha \subseteq \sigma wc (\mathfrak{A} )^*$. As ![]() $\mathfrak{A}$ is commutative and
$\mathfrak{A}$ is commutative and ![]() $\sigma wc (\mathfrak{A} )^*$ is a symmetric bimodule,
$\sigma wc (\mathfrak{A} )^*$ is a symmetric bimodule, ![]() $j_{\mathfrak{A}} \circ D$ must be zero and hence inner.
$j_{\mathfrak{A}} \circ D$ must be zero and hence inner.
Suppose that ![]() $\mathfrak{A}=(\mathfrak{A}_*)^*$ and
$\mathfrak{A}=(\mathfrak{A}_*)^*$ and ![]() $\mathfrak{B} =
(\mathfrak{B}_*)^*$ are dual Banach algebras. We consider the
$\mathfrak{B} =
(\mathfrak{B}_*)^*$ are dual Banach algebras. We consider the ![]() $\ell^1$-direct sum
$\ell^1$-direct sum ![]() $\mathfrak{A} \oplus^1 \mathfrak{B}$ with norm
$\mathfrak{A} \oplus^1 \mathfrak{B}$ with norm ![]() $
|| (a , b) || = || a|| + ||b||$ for
$
|| (a , b) || = || a|| + ||b||$ for ![]() $a \in \mathfrak{A}$ and
$a \in \mathfrak{A}$ and ![]() $b \in
\mathfrak{B}$. This is a dual Banach algebra under pointwise-defined operations and with predual the
$b \in
\mathfrak{B}$. This is a dual Banach algebra under pointwise-defined operations and with predual the ![]() $\ell^\infty$-direct sum
$\ell^\infty$-direct sum ![]() $\mathfrak{A}_* \oplus^\infty \mathfrak{B}_*$, where the norm
$\mathfrak{A}_* \oplus^\infty \mathfrak{B}_*$, where the norm ![]() $||.||_\infty$ is defined through
$||.||_\infty$ is defined through ![]() $ ||(\phi , \psi )||_\infty = \max
( ||\phi|| , ||\psi||)$ for
$ ||(\phi , \psi )||_\infty = \max
( ||\phi|| , ||\psi||)$ for ![]() $\phi \in \mathfrak{A}_*$ and
$\phi \in \mathfrak{A}_*$ and ![]() $\psi \in
\mathfrak{B}_*$. The duality is given by
$\psi \in
\mathfrak{B}_*$. The duality is given by
We write ![]() $ \imath_{\mathfrak{A}} : \mathfrak{A} \longrightarrow \mathfrak{A} \oplus^1 \mathfrak{B}$ for the natural injective homomorphism. It is obvious that
$ \imath_{\mathfrak{A}} : \mathfrak{A} \longrightarrow \mathfrak{A} \oplus^1 \mathfrak{B}$ for the natural injective homomorphism. It is obvious that ![]() $ \imath_{\mathfrak{A}}^*( \varphi , \psi) = \varphi$ for
$ \imath_{\mathfrak{A}}^*( \varphi , \psi) = \varphi$ for ![]() $ (
\varphi , \psi) \in \mathfrak{A}^* \oplus^\infty \mathfrak{B}^* =
(\mathfrak{A} \oplus^1 \mathfrak{B} )^*$. It follows from [Reference Mahmoodi14, Lemma 2.6] that
$ (
\varphi , \psi) \in \mathfrak{A}^* \oplus^\infty \mathfrak{B}^* =
(\mathfrak{A} \oplus^1 \mathfrak{B} )^*$. It follows from [Reference Mahmoodi14, Lemma 2.6] that ![]() $ \sigma wc (\mathfrak{A} \oplus \mathfrak{B} )= \sigma wc (\mathfrak{A})\oplus \sigma w c (\mathfrak{B})$. We also denote by
$ \sigma wc (\mathfrak{A} \oplus \mathfrak{B} )= \sigma wc (\mathfrak{A})\oplus \sigma w c (\mathfrak{B})$. We also denote by ![]() $ \nu_{\mathfrak{A}} : \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* \longrightarrow \sigma wc (\mathfrak{A} )^*$ the adjoint of the natural embedding
$ \nu_{\mathfrak{A}} : \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* \longrightarrow \sigma wc (\mathfrak{A} )^*$ the adjoint of the natural embedding ![]() $ \sigma wc (\mathfrak{A} ) \hookrightarrow \sigma wc (\mathfrak{A} ) \oplus^1 \sigma wc (\mathfrak{B} ) = \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )$, so that
$ \sigma wc (\mathfrak{A} ) \hookrightarrow \sigma wc (\mathfrak{A} ) \oplus^1 \sigma wc (\mathfrak{B} ) = \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )$, so that ![]() $ \nu_{\mathfrak{A}} ( \varphi , \psi) = \varphi$ for
$ \nu_{\mathfrak{A}} ( \varphi , \psi) = \varphi$ for ![]() $ (
\varphi , \psi) \in \sigma wc (\mathfrak{A} ) ^* \oplus^\infty \sigma wc (\mathfrak{B} ) ^* $. Similarly, we define
$ (
\varphi , \psi) \in \sigma wc (\mathfrak{A} ) ^* \oplus^\infty \sigma wc (\mathfrak{B} ) ^* $. Similarly, we define ![]() $
\imath_{\mathfrak{B}}$ and
$
\imath_{\mathfrak{B}}$ and ![]() $\nu_{\mathfrak{B}}$.
$\nu_{\mathfrak{B}}$.
Lemma 4.2. Let ![]() $\mathfrak{A}$ and
$\mathfrak{A}$ and ![]() $\mathfrak{B} $ be dual Banach algebras, and let
$\mathfrak{B} $ be dual Banach algebras, and let ![]() $D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \mathfrak{A}^* \oplus^\infty \mathfrak{B}^*$ be a derivation. Then:
$D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \mathfrak{A}^* \oplus^\infty \mathfrak{B}^*$ be a derivation. Then:
(i)
 $j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D ) =\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) $;
$j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D ) =\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) $;(ii)
 $j_{\mathfrak{B}} \circ ( \imath_{\mathfrak{B}}^* \circ D ) =\nu_{\mathfrak{B}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) $.
$j_{\mathfrak{B}} \circ ( \imath_{\mathfrak{B}}^* \circ D ) =\nu_{\mathfrak{B}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) $.
Proof. We only prove (i). For every ![]() $a \in \mathfrak{A}$,
$a \in \mathfrak{A}$, ![]() $b \in \mathfrak{B} $, and
$b \in \mathfrak{B} $, and ![]() $c \in \sigma wc (\mathfrak{A}) $, we have
$c \in \sigma wc (\mathfrak{A}) $, we have
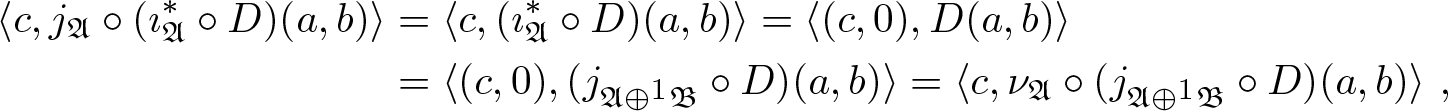 \begin{align*}
\langle c , j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D ) (a, b) \rangle &= \langle c , ( \imath_{\mathfrak{A}}^* \circ D ) (a, b) \rangle = \langle (c , 0 ) , D (a , b) \rangle \\ &= \langle (c , 0 ) , (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , b) \rangle =
\langle c , \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , b) \rangle \ ,
\end{align*}
\begin{align*}
\langle c , j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D ) (a, b) \rangle &= \langle c , ( \imath_{\mathfrak{A}}^* \circ D ) (a, b) \rangle = \langle (c , 0 ) , D (a , b) \rangle \\ &= \langle (c , 0 ) , (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , b) \rangle =
\langle c , \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , b) \rangle \ ,
\end{align*}as required.
Theorem 4.3. Suppose that ![]() $\mathfrak{A}$ and
$\mathfrak{A}$ and ![]() $\mathfrak{B} $ are weakly Connes amenable dual Banach algebras such that
$\mathfrak{B} $ are weakly Connes amenable dual Banach algebras such that ![]() $\mathfrak{A}^2$ and
$\mathfrak{A}^2$ and ![]() $\mathfrak{B}^2$ are
$\mathfrak{B}^2$ are ![]() $w^*$-dense in
$w^*$-dense in ![]() $\mathfrak{A}$ and
$\mathfrak{A}$ and ![]() $\mathfrak{B}$, respectively. Then,
$\mathfrak{B}$, respectively. Then, ![]() $\mathfrak{A} \oplus^1 \mathfrak{B}$ is weakly Connes amenable.
$\mathfrak{A} \oplus^1 \mathfrak{B}$ is weakly Connes amenable.
Proof. Take a derivation ![]() $D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow (\mathfrak{A}
\oplus^1 \mathfrak{B} )^* = \mathfrak{A}^* \oplus^\infty \mathfrak{B}^*$ for which
$D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow (\mathfrak{A}
\oplus^1 \mathfrak{B} )^* = \mathfrak{A}^* \oplus^\infty \mathfrak{B}^*$ for which  $j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* $ is
$j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D :\mathfrak{A} \oplus^1 \mathfrak{B} \longrightarrow \sigma wc (\mathfrak{A} \oplus^1 \mathfrak{B} )^* = \sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* $ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. Then,
$w^*$ continuous. Then, ![]() $ \imath_{\mathfrak{A}}^* \circ D \circ \imath_{\mathfrak{A}} :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ is a derivation. An easy calculation shows that
$ \imath_{\mathfrak{A}}^* \circ D \circ \imath_{\mathfrak{A}} :\mathfrak{A} \longrightarrow \mathfrak{A}^*$ is a derivation. An easy calculation shows that ![]() $j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D \circ \imath_{\mathfrak{A}} ) : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is
$j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D \circ \imath_{\mathfrak{A}} ) : \mathfrak{A} \longrightarrow \sigma wc (\mathfrak{A} )^*$ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. Since
$w^*$ continuous. Since ![]() $\mathfrak{A}$ is weakly Connes amenable, there exists
$\mathfrak{A}$ is weakly Connes amenable, there exists ![]() $ \varphi \in \sigma wc (\mathfrak{A} )^*$ such that
$ \varphi \in \sigma wc (\mathfrak{A} )^*$ such that ![]() $j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D)
(a , 0) = ad_\varphi (a)$ and then, by Lemma 4.2(i),
$j_{\mathfrak{A}} \circ ( \imath_{\mathfrak{A}}^* \circ D)
(a , 0) = ad_\varphi (a)$ and then, by Lemma 4.2(i), ![]() $\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , 0) = ad_\varphi (a)$ for every
$\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , 0) = ad_\varphi (a)$ for every ![]() $a \in \mathfrak{A}$. We regard
$a \in \mathfrak{A}$. We regard ![]() $\varphi = (\varphi , 0 )$ as an element of
$\varphi = (\varphi , 0 )$ as an element of ![]() $\sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* $. Then it is easily checked that
$\sigma wc (\mathfrak{A} )^* \oplus^\infty \sigma wc (\mathfrak{B} )^* $. Then it is easily checked that ![]() $\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ ( D - ad_\varphi ) ) (a , 0) = 0$. So, by replacing D by
$\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ ( D - ad_\varphi ) ) (a , 0) = 0$. So, by replacing D by ![]() $D-ad_\varphi$, we may suppose that
$D-ad_\varphi$, we may suppose that ![]() $\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , 0) =0$ for every
$\nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a , 0) =0$ for every ![]() $a \in \mathfrak{A}$. For each
$a \in \mathfrak{A}$. For each ![]() $ a_1 , a_2 \in \mathfrak{A}$,
$ a_1 , a_2 \in \mathfrak{A}$, ![]() $ a \in \sigma wc (\mathfrak{A} )$ and
$ a \in \sigma wc (\mathfrak{A} )$ and ![]() $b \in \sigma wc (\mathfrak{B} )$, we see that
$b \in \sigma wc (\mathfrak{B} )$, we see that
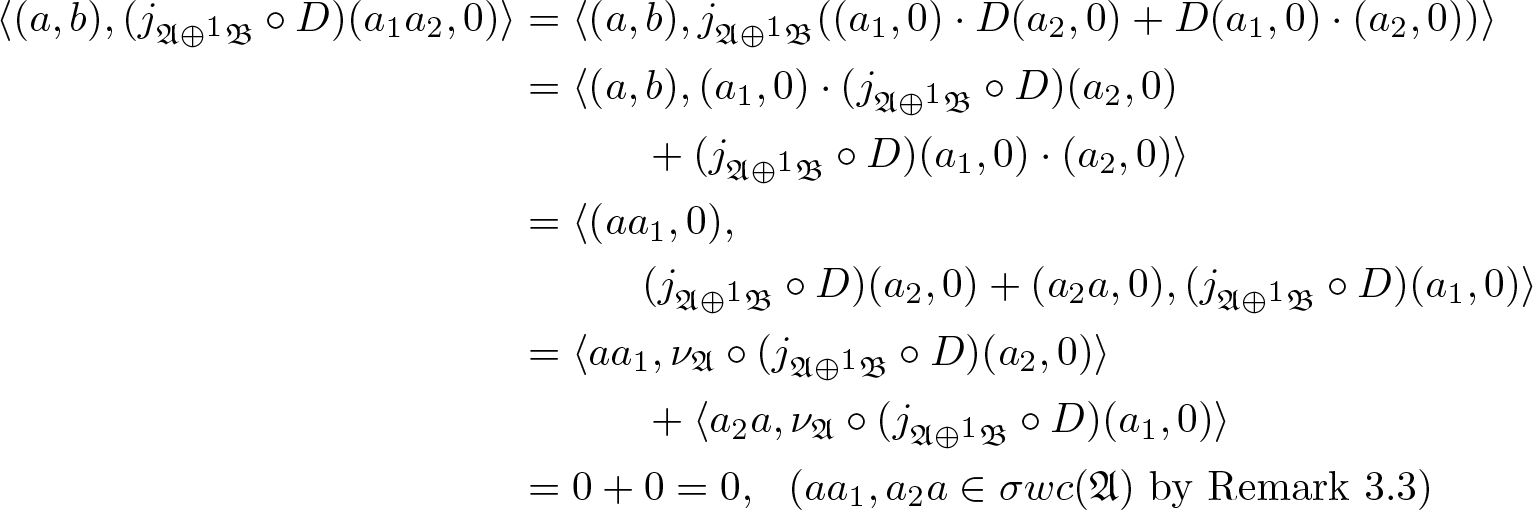 \begin{align*}
\langle (a , b) , (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 a_2, 0) \rangle
&= \langle (a , b) , j_{\mathfrak{A} \oplus^1 \mathfrak{B}} ( ( a_1 , 0) \cdot D(a_2 , 0 )+ D(a_1 , 0 ) \cdot (a_2 , 0 ) ) \rangle \\ &= \langle (a , b) , ( a_1 , 0) \cdot (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 )\nonumber \\ & \quad\qquad + (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \cdot (a_2 , 0 ) \rangle \\
&= \langle (a a_1 , 0),\nonumber \\ & \quad\qquad (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 ) + ( a_2 a , 0), (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \rangle \\ &= \langle a a_1, \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 ) \rangle\nonumber \\
& \quad\qquad + \langle a_2 a, \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \rangle \\ &= 0 + 0 = 0 , \ \ ( a a_1, a_2 a \in \sigma wc (\mathfrak{A} ) \ \text{by Remark} \ 3.3 )
\end{align*}
\begin{align*}
\langle (a , b) , (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 a_2, 0) \rangle
&= \langle (a , b) , j_{\mathfrak{A} \oplus^1 \mathfrak{B}} ( ( a_1 , 0) \cdot D(a_2 , 0 )+ D(a_1 , 0 ) \cdot (a_2 , 0 ) ) \rangle \\ &= \langle (a , b) , ( a_1 , 0) \cdot (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 )\nonumber \\ & \quad\qquad + (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \cdot (a_2 , 0 ) \rangle \\
&= \langle (a a_1 , 0),\nonumber \\ & \quad\qquad (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 ) + ( a_2 a , 0), (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \rangle \\ &= \langle a a_1, \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_2 , 0 ) \rangle\nonumber \\
& \quad\qquad + \langle a_2 a, \nu_{\mathfrak{A}} \circ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 , 0 ) \rangle \\ &= 0 + 0 = 0 , \ \ ( a a_1, a_2 a \in \sigma wc (\mathfrak{A} ) \ \text{by Remark} \ 3.3 )
\end{align*}
and whence ![]() $ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 a_2, 0) = 0$ for all
$ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a_1 a_2, 0) = 0$ for all ![]() $ a_1 , a_2 \in \mathfrak{A}$. Now, it follows from
$ a_1 , a_2 \in \mathfrak{A}$. Now, it follows from ![]() $w^*$-density of
$w^*$-density of ![]() $\mathfrak{A}^2$ and
$\mathfrak{A}^2$ and ![]() $w^*$-continuity of
$w^*$-continuity of ![]() $ j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D $ that
$ j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D $ that ![]() $ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a, 0) = 0$ for every
$ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (a, 0) = 0$ for every ![]() $ a \in \mathfrak{A}$.
$ a \in \mathfrak{A}$.
A similar argument, with ![]() $\mathfrak{B} $ in place of
$\mathfrak{B} $ in place of ![]() $\mathfrak{A} $, shows that
$\mathfrak{A} $, shows that ![]() $ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (0, b) = 0$ for every
$ (j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D ) (0, b) = 0$ for every ![]() $ b \in \mathfrak{B}$. It follows that
$ b \in \mathfrak{B}$. It follows that ![]() $ j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D = 0$, and hence
$ j_{\mathfrak{A} \oplus^1 \mathfrak{B}} \circ D = 0$, and hence ![]() $\mathfrak{A} \oplus^1 \mathfrak{B}$ is weakly Connes amenable.
$\mathfrak{A} \oplus^1 \mathfrak{B}$ is weakly Connes amenable.
Proposition 4.4. Let ![]() $\mathfrak{A}$ be a commutative Banach algebra, let
$\mathfrak{A}$ be a commutative Banach algebra, let ![]() $\mathfrak{B} $ be a dual Banach algebra, and let
$\mathfrak{B} $ be a dual Banach algebra, and let ![]() $\theta: \mathfrak{A} \longrightarrow
\mathfrak{B}$ be a (continuous) homomorphism with
$\theta: \mathfrak{A} \longrightarrow
\mathfrak{B}$ be a (continuous) homomorphism with ![]() $w^*$-dense range. If
$w^*$-dense range. If ![]() $\mathfrak{A}$ is weakly amenable, then
$\mathfrak{A}$ is weakly amenable, then ![]() $\mathfrak{B} $ is weakly Connes amenable.
$\mathfrak{B} $ is weakly Connes amenable.
Proof. Take a derivation ![]() $D
:\mathfrak{B} \longrightarrow \mathfrak{B}^* $ such that
$D
:\mathfrak{B} \longrightarrow \mathfrak{B}^* $ such that ![]() $j_{\mathfrak{B}} \circ D : \mathfrak{B} \longrightarrow
\sigma wc (\mathfrak{B} )^* $ is
$j_{\mathfrak{B}} \circ D : \mathfrak{B} \longrightarrow
\sigma wc (\mathfrak{B} )^* $ is ![]() $w^*$-
$w^*$-![]() $w^*$ continuous. Then,
$w^*$ continuous. Then, ![]() $(j_{\mathfrak{B}} \circ D ) \circ \theta :
\mathfrak{A} \longrightarrow \sigma wc (\mathfrak{B} )^*$ is a derivation. By [Reference Dales2, Theorem 2.8.63 (iii)],
$(j_{\mathfrak{B}} \circ D ) \circ \theta :
\mathfrak{A} \longrightarrow \sigma wc (\mathfrak{B} )^*$ is a derivation. By [Reference Dales2, Theorem 2.8.63 (iii)], ![]() $(j_{\mathfrak{B}} \circ D ) \circ \theta= 0$. From
$(j_{\mathfrak{B}} \circ D ) \circ \theta= 0$. From ![]() $w^*$-continuity of
$w^*$-continuity of ![]() $j_{\mathfrak{B}} \circ D$ and
$j_{\mathfrak{B}} \circ D$ and ![]() $w^*$-density of the range of θ, we conclude that
$w^*$-density of the range of θ, we conclude that ![]() $j_{\mathfrak{B}} \circ D = 0$, as required.
$j_{\mathfrak{B}} \circ D = 0$, as required.
Let ![]() $\mathfrak{A}$ be a Banach algebra. We write
$\mathfrak{A}$ be a Banach algebra. We write ![]() $ WAP
(\mathfrak{A}^*)$ for the space of all weakly almost periodic functionals on
$ WAP
(\mathfrak{A}^*)$ for the space of all weakly almost periodic functionals on ![]() $\mathfrak{A}$. It is noted by Runde that
$\mathfrak{A}$. It is noted by Runde that ![]() $ WAP (\mathfrak{A}^*)^*$ is a dual Banach algebra with a universal property [Reference Runde16, Theorem 4.10]. Later, Daws called
$ WAP (\mathfrak{A}^*)^*$ is a dual Banach algebra with a universal property [Reference Runde16, Theorem 4.10]. Later, Daws called ![]() $
WAP (\mathfrak{A}^*)^*$ the dual Banach algebra enveloping algebra of
$
WAP (\mathfrak{A}^*)^*$ the dual Banach algebra enveloping algebra of ![]() $\mathfrak{A}$ [Reference Daws6, Definition 2.10]. There is a (continuous) homomorphism
$\mathfrak{A}$ [Reference Daws6, Definition 2.10]. There is a (continuous) homomorphism ![]() $ \kappa : \mathfrak{A} \longrightarrow WAP (\mathfrak{A}^*)^*$ whose range is
$ \kappa : \mathfrak{A} \longrightarrow WAP (\mathfrak{A}^*)^*$ whose range is ![]() $w^*$-dense. Indeed, the map κ was obtained by composing the canonical inclusion
$w^*$-dense. Indeed, the map κ was obtained by composing the canonical inclusion ![]() $ \mathfrak{A} \longrightarrow \mathfrak{A}^{**}$ with the adjoint of the inclusion map
$ \mathfrak{A} \longrightarrow \mathfrak{A}^{**}$ with the adjoint of the inclusion map ![]() $ WAP (\mathfrak{A}^*) \hookrightarrow \mathfrak{A} ^*$ [Reference Runde16].
$ WAP (\mathfrak{A}^*) \hookrightarrow \mathfrak{A} ^*$ [Reference Runde16].
Corollary 4.5. Let ![]() $\mathfrak{A}$ be a commutative, weakly amenable Banach algebra. Then,
$\mathfrak{A}$ be a commutative, weakly amenable Banach algebra. Then, ![]() $ WAP (\mathfrak{A}^*)^*$ is weakly Connes amenable.
$ WAP (\mathfrak{A}^*)^*$ is weakly Connes amenable.
Proof. We apply Proposition 4.4 for the canonical homomorphism ![]() $ \kappa : \mathfrak{A} \longrightarrow WAP (\mathfrak{A}^*)^*$.
$ \kappa : \mathfrak{A} \longrightarrow WAP (\mathfrak{A}^*)^*$.
5. More examples
In this section, we give some examples to compare weak Connes amenability and some older notions such as Connes amenability, weak amenability and pseudo (Connes) amenability.
Example 5.1. It is well known that ![]() $\ell^1= \ell^1( \mathbb{N})$ with pointwise multiplication is a commutative, weakly amenable dual Banach algebra. It follows from Proposition 3.6 that
$\ell^1= \ell^1( \mathbb{N})$ with pointwise multiplication is a commutative, weakly amenable dual Banach algebra. It follows from Proposition 3.6 that ![]() $\ell^1$ is weakly Connes amenable. Further,
$\ell^1$ is weakly Connes amenable. Further, ![]() $WAP((\ell^1)^*)^* = WAP(\ell^\infty)^*$ is also weakly Connes amenable, by Corollary 4.5. However, they fail to be Connes amenable because of the lack of an identity.
$WAP((\ell^1)^*)^* = WAP(\ell^\infty)^*$ is also weakly Connes amenable, by Corollary 4.5. However, they fail to be Connes amenable because of the lack of an identity.
Example 5.2. Consider the semigroup ![]() $\mathbb{N}_{\vee}$ which is
$\mathbb{N}_{\vee}$ which is ![]() $\mathbb{N }$ with the operation
$\mathbb{N }$ with the operation ![]() $m \vee n := \max \{m, n\}$,
$m \vee n := \max \{m, n\}$, ![]() $(m, n \in \mathbb{N}) $. It is known that
$(m, n \in \mathbb{N}) $. It is known that ![]() $\ell^1( \mathbb{N}_{\vee})$ is a commutative, weakly amenable dual Banach algebra. An argument similar to Example 5.1 shows that both
$\ell^1( \mathbb{N}_{\vee})$ is a commutative, weakly amenable dual Banach algebra. An argument similar to Example 5.1 shows that both ![]() $\ell^1( \mathbb{N}_{\vee})$ and
$\ell^1( \mathbb{N}_{\vee})$ and ![]() $WAP(\ell^1(
\mathbb{N}_{\vee})^*)^*$ are weakly Connes amenable. Notice that none of them are Connes amenable by [Reference Daws5, Theorem 5.13] and [Reference Daws6, p. 262], respectively.
$WAP(\ell^1(
\mathbb{N}_{\vee})^*)^*$ are weakly Connes amenable. Notice that none of them are Connes amenable by [Reference Daws5, Theorem 5.13] and [Reference Daws6, p. 262], respectively.
Example 5.3. We denote by ![]() $\mathbb{N}_{\wedge}$ the semigroup
$\mathbb{N}_{\wedge}$ the semigroup ![]() $\mathbb{N }$ with the operation
$\mathbb{N }$ with the operation ![]() $m \wedge n := \min
\{m, n\}$,
$m \wedge n := \min
\{m, n\}$, ![]() $(m, n \in \mathbb{N}) $. It is known that
$(m, n \in \mathbb{N}) $. It is known that ![]() $\ell^1(
\mathbb{N}_{\wedge})$ is a commutative, weakly amenable Banach algebra. By Corollary 4.5,
$\ell^1(
\mathbb{N}_{\wedge})$ is a commutative, weakly amenable Banach algebra. By Corollary 4.5, ![]() $WAP(\ell^1( \mathbb{N}_{\wedge})^*)^*$ is weakly Connes amenable. It was shown in [Reference Daws6, Theorem 7.6] that
$WAP(\ell^1( \mathbb{N}_{\wedge})^*)^*$ is weakly Connes amenable. It was shown in [Reference Daws6, Theorem 7.6] that ![]() $WAP(\ell^1( \mathbb{N}_{\wedge})^*)^*$ is not Connes amenable.
$WAP(\ell^1( \mathbb{N}_{\wedge})^*)^*$ is not Connes amenable.
Let ![]() $\mathfrak{A}$ be a dual Banach algebra. Composing the canonical inclusion
$\mathfrak{A}$ be a dual Banach algebra. Composing the canonical inclusion ![]() $ \mathfrak{A} \hat{\otimes} \mathfrak{A}
\longrightarrow ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^{**}$ with the quotient map
$ \mathfrak{A} \hat{\otimes} \mathfrak{A}
\longrightarrow ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^{**}$ with the quotient map ![]() $ ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^{**}
\longrightarrow \sigma wc ( ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$, we obtain an
$ ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^{**}
\longrightarrow \sigma wc ( ( \mathfrak{A} \hat{\otimes} \mathfrak{A})^*)^*$, we obtain an ![]() $\mathfrak{A}$-bimodule homomorphism
$\mathfrak{A}$-bimodule homomorphism ![]() $\zeta : \mathfrak{A} \hat{\otimes} \mathfrak{A} \longrightarrow
\sigma wc ( (\mathfrak{A} \hat{\otimes} \mathfrak{A}) ^*)^*$ with
$\zeta : \mathfrak{A} \hat{\otimes} \mathfrak{A} \longrightarrow
\sigma wc ( (\mathfrak{A} \hat{\otimes} \mathfrak{A}) ^*)^*$ with ![]() $w^*$-dense range.
$w^*$-dense range.
Definition 5.4. ([Reference Mahmoodi14]) A dual Banach algebra ![]() $\mathfrak{A}$ is pseudo Connes amenable if there exists a net
$\mathfrak{A}$ is pseudo Connes amenable if there exists a net ![]() $(m_\alpha)_\alpha$ in
$(m_\alpha)_\alpha$ in ![]() $ \mathfrak{A} \hat{\otimes} \mathfrak{A}$, called an approximate
$ \mathfrak{A} \hat{\otimes} \mathfrak{A}$, called an approximate ![]() $\sigma
wc$-diagonal for
$\sigma
wc$-diagonal for ![]() $\mathfrak{A}$, such that
$\mathfrak{A}$, such that  $ a \ . \ \zeta (m_\alpha) - \zeta (m_\alpha) \ . \
a \stackrel{w^*} \longrightarrow 0 $, and
$ a \ . \ \zeta (m_\alpha) - \zeta (m_\alpha) \ . \
a \stackrel{w^*} \longrightarrow 0 $, and  $a
\pi_{\sigma wc} (m_\alpha) \stackrel{w^*} \longrightarrow a$ for every
$a
\pi_{\sigma wc} (m_\alpha) \stackrel{w^*} \longrightarrow a$ for every ![]() $a \in \mathfrak{A}$.
$a \in \mathfrak{A}$.
We write ![]() $ \mathfrak{A}^\sharp$ for the unitization of an algebra
$ \mathfrak{A}^\sharp$ for the unitization of an algebra ![]() $
\mathfrak{A}$.
$
\mathfrak{A}$.
Theorem 5.5. Let G be a non-discrete locally compact group, and set ![]() $ \mathfrak{A} := M(G) \oplus^1
(\ell^1)^\sharp$. Then:
$ \mathfrak{A} := M(G) \oplus^1
(\ell^1)^\sharp$. Then:
(i)
 $ \mathfrak{A} $ is not weakly amenable;
$ \mathfrak{A} $ is not weakly amenable;(ii)
 $ \mathfrak{A} $ is not pseudo amenable;
$ \mathfrak{A} $ is not pseudo amenable;(iii)
 $ \mathfrak{A} $ is not Connes amenable;
$ \mathfrak{A} $ is not Connes amenable;(iv)
 $ \mathfrak{A} $ is not pseudo Connes amenable;
$ \mathfrak{A} $ is not pseudo Connes amenable;(v)
 $ \mathfrak{A} $ is weakly Connes amenable.
$ \mathfrak{A} $ is weakly Connes amenable.
(i) If
 $ \mathfrak{A}$ were weakly amenable, then so is its image under the natural projection
$ \mathfrak{A}$ were weakly amenable, then so is its image under the natural projection  $ \mathcal{P}_{M(G)} : \mathfrak{A} \longrightarrow M(G) $ by [Reference Lau and Loy13, Lemma 2.3]. However, this is not possible for non-discrete groups [Reference Runde17, Theorem 4.2.13].
$ \mathcal{P}_{M(G)} : \mathfrak{A} \longrightarrow M(G) $ by [Reference Lau and Loy13, Lemma 2.3]. However, this is not possible for non-discrete groups [Reference Runde17, Theorem 4.2.13].(ii) By [Reference Ghahramani and Zhang9, Theorem 3.1] and [Reference Dales, Loy and Zang4, Theorem 4.1],
 $(\ell^1)^\sharp$ is not pseudo amenable. As
$(\ell^1)^\sharp$ is not pseudo amenable. As  $(\ell^1)^\sharp$ is the image of
$(\ell^1)^\sharp$ is the image of  $ \mathfrak{A}$ under the projection
$ \mathfrak{A}$ under the projection  $ \mathcal{P}_{(\ell^1)^\sharp} : \mathfrak{A} \longrightarrow (\ell^1)^\sharp $,
$ \mathcal{P}_{(\ell^1)^\sharp} : \mathfrak{A} \longrightarrow (\ell^1)^\sharp $,  $ \mathfrak{A}$ cannot be pseudo amenable by [Reference Ghahramani and Zhang9, Proposition 2.2].
$ \mathfrak{A}$ cannot be pseudo amenable by [Reference Ghahramani and Zhang9, Proposition 2.2].(iii) If
 $ \mathfrak{A}$ were Connes amenable, then so is
$ \mathfrak{A}$ were Connes amenable, then so is  $(\ell^1)^\sharp$, its image under the natural projection
$(\ell^1)^\sharp$, its image under the natural projection  $ \mathcal{P}_{(\ell^1)^\sharp} : \mathfrak{A} \longrightarrow (\ell^1)^\sharp $ by [Reference Runde15, Proposition 4.2], which is not the case.
$ \mathcal{P}_{(\ell^1)^\sharp} : \mathfrak{A} \longrightarrow (\ell^1)^\sharp $ by [Reference Runde15, Proposition 4.2], which is not the case.(iv) Towards a contradiction, suppose that
 $ \mathfrak{A}$ is pseudo Connes amenable. Then
$ \mathfrak{A}$ is pseudo Connes amenable. Then  $(\ell^1)^\sharp$, the image of
$(\ell^1)^\sharp$, the image of  $ \mathfrak{A}$ under
$ \mathfrak{A}$ under  $\mathcal{P}_{(\ell^1)^\sharp}$, must be pseudo Connes amenable by [Reference Mahmoodi14, Proposition 4.5]. But, it follows from [Reference Mahmoodi14, Theorems 3.2 and 5.1] that
$\mathcal{P}_{(\ell^1)^\sharp}$, must be pseudo Connes amenable by [Reference Mahmoodi14, Proposition 4.5]. But, it follows from [Reference Mahmoodi14, Theorems 3.2 and 5.1] that  $(\ell^1)^\sharp$ is not pseudo Connes amenable.
$(\ell^1)^\sharp$ is not pseudo Connes amenable.(v) Weak amenability of
 $\ell^1$ implies that of
$\ell^1$ implies that of  $(\ell^1)^\sharp$. By Theorem 3.6,
$(\ell^1)^\sharp$. By Theorem 3.6,  $(\ell^1)^\sharp$ is weakly Connes amenable. Then, using Theorem 3.7, weak Connes amenability of
$(\ell^1)^\sharp$ is weakly Connes amenable. Then, using Theorem 3.7, weak Connes amenability of  $ \mathfrak{A}$ is a consequence of Theorem 4.3.
$ \mathfrak{A}$ is a consequence of Theorem 4.3.
Acknowledgements
I am grateful to the referee for pointing out some errors in response to previous versions of this work, for discovering some inaccuracies in the proof of Proposition 4.1 and Theorem 5.5, and for directing me to [Reference Lau and Loy13], as well as for several valuable suggestions which led to the improvement of the presentation of the paper. I would also like to thank Jared White for bringing [Reference Despic and Ghahramani7] to my attention and constructive discussions on Theorem 3.7.
Competing interests
The author declare no competing interests.