Let 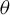 $\theta $ be an irrational real number. The map
$\theta $ be an irrational real number. The map 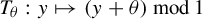 $T_\theta : y \mapsto (y+\theta ) \,\mod \!\!\: 1$ from the unit interval
$T_\theta : y \mapsto (y+\theta ) \,\mod \!\!\: 1$ from the unit interval 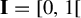 $\mathbf {I} = [0,1[$ (endowed with the Lebesgue measure) to itself is ergodic. In 2002, Rudolph and Hoffman showed in [Uniform endomorphisms which are isomorphic to a Bernoulli shift. Ann. of Math. (2) 156(1) (2002), 79–101] that the measure-preserving map
$\mathbf {I} = [0,1[$ (endowed with the Lebesgue measure) to itself is ergodic. In 2002, Rudolph and Hoffman showed in [Uniform endomorphisms which are isomorphic to a Bernoulli shift. Ann. of Math. (2) 156(1) (2002), 79–101] that the measure-preserving map 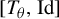 $[T_\theta ,\mathrm {Id}]$ is isomorphic to a one-sided dyadic Bernoulli shift. Their proof is not constructive. A few years before, Parry [Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] had provided an explicit isomorphism under the assumption that
$[T_\theta ,\mathrm {Id}]$ is isomorphic to a one-sided dyadic Bernoulli shift. Their proof is not constructive. A few years before, Parry [Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] had provided an explicit isomorphism under the assumption that 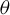 $\theta $ is extremely well approached by the rational numbers, namely,
$\theta $ is extremely well approached by the rational numbers, namely, 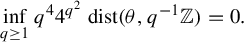 $$ \begin{align*}\inf_{q \ge 1} q^44^{q^2}~\mathrm{dist}(\theta,q^{-1}\mathbb{Z}) = 0.\end{align*} $$
$$ \begin{align*}\inf_{q \ge 1} q^44^{q^2}~\mathrm{dist}(\theta,q^{-1}\mathbb{Z}) = 0.\end{align*} $$
Whether the explicit map considered by Parry is an isomorphism or not in the general case was still an open question. In Leuridan [Bernoulliness of  $[T,\mathrm {Id}]$ when T is an irrational rotation: towards an explicit isomorphism. Ergod. Th. & Dynam. Sys. 41(7) (2021), 2110–2135] we relaxed Parry’s condition into
$[T,\mathrm {Id}]$ when T is an irrational rotation: towards an explicit isomorphism. Ergod. Th. & Dynam. Sys. 41(7) (2021), 2110–2135] we relaxed Parry’s condition into 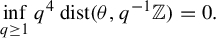 $$ \begin{align*}\inf_{q \ge 1} q^4~\mathrm{dist}(\theta,q^{-1}\mathbb{Z}) = 0.\end{align*} $$
$$ \begin{align*}\inf_{q \ge 1} q^4~\mathrm{dist}(\theta,q^{-1}\mathbb{Z}) = 0.\end{align*} $$
In the present paper, we remove the condition by showing that the explicit map considered by Parry is always an isomorphism. With a few adaptations, the same method works with 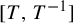 $[T,T^{-1}]$.
$[T,T^{-1}]$.
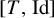 $[T,\mathrm {Id}]$ and
$[T,\mathrm {Id}]$ and 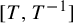 $[T,T^{-1}]$ are Bernoulli: explicit isomorphisms
$[T,T^{-1}]$ are Bernoulli: explicit isomorphisms
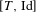 $[T,\text{Id}]$ when
$[T,\text{Id}]$ when  $T$ is an irrational rotation: towards an explicit isomorphism
$T$ is an irrational rotation: towards an explicit isomorphism