We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A celebrated result by Bourgain and Wierdl states that ergodic averages along primes converge almost everywhere for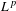 
$L^{p}$-functions, 
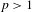$p>1$, with a polynomial version by Wierdl and Nair. Using an anti-correlation result for the von Mangoldt function due to Green and Tao, we observe everywhere convergence of such averages for nilsystems and continuous functions.
