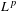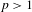Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Buczolich, Zoltán
and
Eisner, Tanja
2021.
Divergence of weighted square averages in L1.
Advances in Mathematics,
Vol. 384,
Issue. ,
p.
107727.
Adamczewski, Boris
and
Konieczny, Jakub
2023.
Bracket words: A generalisation of Sturmian words arising from generalised polynomials.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 7,
p.
4979.