We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that, if X is a variety over an uncountable algebraically closed field k of characteristic zero, then any irreducible exceptional divisor E on a resolution of singularities of X which is not uniruled, belongs to the image of the Nash map, i.e. corresponds to an irreducible component of the space of arcs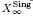 
on X centred in Sing X. This reduces the Nash problem of arcs to understanding which uniruled essential divisors are in the image of the Nash map, more generally, how to determine the uniruled essential divisors from the space of arcs.
