Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Reguera, Ana J.
2012.
Arcs and wedges on rational surface singularities.
Journal of Algebra,
Vol. 366,
Issue. ,
p.
126.
de Fernex, Tommaso
2013.
Three-dimensional counter-examples to the Nash problem.
Compositio Mathematica,
Vol. 149,
Issue. 9,
p.
1519.
de Fernex, Tommaso
and
Docampo, Roi
2016.
Terminal valuations and the Nash problem.
Inventiones mathematicae,
Vol. 203,
Issue. 1,
p.
303.
Docampo, Roi
and
Nigro, Antonio
2017.
The arc space of the Grassmannian.
Advances in Mathematics,
Vol. 306,
Issue. ,
p.
1269.
Reguera, Ana J.
2018.
Coordinates at stable points of the space of arcs.
Journal of Algebra,
Vol. 494,
Issue. ,
p.
40.
Chambert-Loir, Antoine
Nicaise, Johannes
and
Sebag, Julien
2018.
Motivic Integration.
Vol. 325,
Issue. ,
p.
363.
Reguera, Ana J.
2023.
Arc spaces and wedge spaces for toric varieties.
Annales de l'Institut Fourier,
Vol. 73,
Issue. 5,
p.
2135.
Ishii, Shihoko
2023.
Handbook of Geometry and Topology of Singularities IV.
p.
161.
Bourqui, David
and
Morán Cañón, Mario
2023.
Deformations of arcs and comparison of formal neighborhoods for a curve singularity.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Bourqui, David
Langlois, Kevin
and
Mourtada, Hussein
2024.
The Nash problem for torus actions of complexity one.
Journal für die reine und angewandte Mathematik (Crelles Journal),

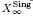 on
on 