Refine search
Actions for selected content:
8 results
On the Ziv–Merhav theorem beyond Markovianity I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 891-915
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Machine Learning with Spark
- from Part III - Machine Learning for Big Data
-
- Book:
- Large-Scale Data Analytics with Python and Spark
- Published online:
- 15 December 2023
- Print publication:
- 23 November 2023, pp 177-211
-
- Chapter
- Export citation
DISTRIBUTION-FREE CONFIDENCE INTERVALS FOR FUNCTIONS OF QUANTILES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 520-522
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
11 - Principles of point estimation
- from Part B - Estimation And Inference
-
- Book:
- Statistics
- Published online:
- 11 June 2020
- Print publication:
- 08 November 2018, pp 437-484
-
- Chapter
- Export citation
Estimation of anisotropic Gaussian fields through Radon transform
-
- Journal:
- ESAIM: Probability and Statistics / Volume 12 / 2008
- Published online by Cambridge University Press:
- 13 November 2007, pp. 30-50
- Print publication:
- 2008
-
- Article
- Export citation
Comparative analysis of estimators for wind direction standard deviation
-
- Journal:
- Meteorological Applications / Volume 13 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 29-41
- Print publication:
- March 2006
-
- Article
- Export citation
The weak convergence of a class of estimators of the variance function of a two-dimensional Poisson process
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 2 / June 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 433-439
- Print publication:
- June 1978
-
- Article
- Export citation
On the weak convergence of a class of estimators of the variance-time curve of a weakly stationary point process
-
- Journal:
- Journal of Applied Probability / Volume 14 / Issue 1 / March 1977
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-126
- Print publication:
- March 1977
-
- Article
- Export citation
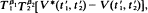 where
where 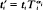 and
and 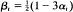 for 0 <
for 0 < 