Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ripley, B. D.
1979.
Tests of 'Randomness' for Spatial Point Patterns.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 41,
Issue. 3,
p.
368.
Adelfio, Giada
and
Schoenberg, Frederic Paik
2009.
Point process diagnostics based on weighted second-order statistics and their asymptotic properties.
Annals of the Institute of Statistical Mathematics,
Vol. 61,
Issue. 4,
p.
929.

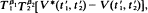 where
where 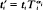 and
and 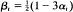 for 0 <
for 0 < 