1 results
The Topological Nature of Two Noguchi Theorems on Sequences of Holomorphic Mappings Between Complex Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 6 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1240-1252
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
-
Let C,D,D* be, respectively, the complex plane, {z ∈ C : |z| < 1}, and D — {0}. If P1(C) is the Riemann sphere, the Big Picard theorem states that if ƒ:D* → P1(C) is holomorphic and P1(C) → ƒ(D*) n a s more than two elements, then ƒ has a holomorphic extension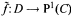
. Under certain assumptions on M, A and X ⊂ Y, combined efforts of Kiernan, Kobayashi and Kwack extended the theorem to all holomorphic ƒ: M → A → X. Relying on these results, measure theoretic theorems of Lelong and Wirtinger, and other properties of complex spaces, Noguchi proved in this context that if ƒ: M → A → X and ƒn: M → A → X are holomorphic for each n and ƒn → ƒ, then 
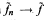. In this paper we show that all of these theorems may be significantly generalized and improved by purely topological methods. We also apply our results to present a topological generalization of a classical theorem of Vitali from one variable complex function theory.
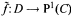. Under certain assumptions on 
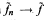. In this paper we show that all of these theorems may be significantly generalized and improved by purely topological methods. We also apply our results to present a topological generalization of a classical theorem of Vitali from one variable complex function theory.