Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T16:23:01.103Z Has data issue: false hasContentIssue false
  • English
  • Français

The Topological Nature of Two Noguchi Theorems on Sequences of Holomorphic Mappings Between Complex Spaces

Published online by Cambridge University Press:  20 November 2018

James E. Joseph  and
Myung H. Kwack
James E. Joseph
Affiliation:
Department of Mathematics Howard University Washington, D.C 20059 U.S.A. e-mail: jjoseph@scs.howard.edu
Myung H. Kwack
Affiliation:
Department of Mathematics Howard University Washington, D.C 20059 U.S.A. e-mail: jjoseph@scs.howard.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let C,D,D* be, respectively, the complex plane, {z ∈ C : |z| < 1}, and D — {0}. If P1(C) is the Riemann sphere, the Big Picard theorem states that if ƒ:D* → P1(C) is holomorphic and P1(C) → ƒ(D*) n a s more than two elements, then ƒ has a holomorphic extension 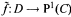. Under certain assumptions on M, A and X ⊂ Y, combined efforts of Kiernan, Kobayashi and Kwack extended the theorem to all holomorphic ƒ: M → A → X. Relying on these results, measure theoretic theorems of Lelong and Wirtinger, and other properties of complex spaces, Noguchi proved in this context that if ƒ: M → A → X and ƒn: M → A → X are holomorphic for each n and ƒn → ƒ, then 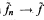. In this paper we show that all of these theorems may be significantly generalized and improved by purely topological methods. We also apply our results to present a topological generalization of a classical theorem of Vitali from one variable complex function theory.

Keywords

32H1532H2054C3554C2054D50complex spaces, big Picard theoremcontinuous extensionsholomorphic mapsfc-spacesfunction spacescompact-open topologyeven continuityAlexandroff one-point compactificationAscoli Theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 6 , 01 December 1995 , pp. 1240 - 1252
Copyright
Copyright © Canadian Mathematical Society 1995

References

[B] Boas, R., Invitation to Complex Analysis, Random House, New York, 1987.Google Scholar
[B-D] Bourbaki, N. and Dieudonné, J., Note de Tèratopologie II, Rev. Questions Sci. 77(1939), 180–181.Google Scholar
[B-Y] Bagley, R.W. and Yang, J.S., On k-spaces and function spaces, Proc. Amer. Math. Soc. 17(1966), 703— 705.Google Scholar
[D] Dugundji, J., Topology, Allyn and Bacon, Boston, 1966.Google Scholar
[J-K] Joseph, J. and Kwack, M., Hyperbolic imbedding and spaces of continuous extensions of holomorphic maps, J. Geom. Anal. 4(1994), 361–378.Google Scholar
[Ke] Kelley, J.L., Topology, VanNostrand, Princeton, New Jersey, 1955.Google Scholar
[Ki] Kiernan, P., Extensions of holomorphic maps, Trans. Amer. Math. Soc. 172(1972), 347–355.Google Scholar
[Ko] Kobayashi, S., Hyperbolic Manifolds and Holomorphic Mappings, Marcel Dekker, New York, 1970.Google Scholar
[Kw] Kwack, M., Generalizations of the Big Picard theorem, Ann. of Math. (2) 90(1969), 9–22.Google Scholar
[K-T] Klein, E. and Thompson, A.C., Theory of Correspondences, John Wiley, New York, 1984.Google Scholar
[L] Lang, S., Introduction to Complex Hyperbolic Spaces, Springer-Verlag, New York, 1987.Google Scholar
[No 1] Noguchi, J., Hyperbolic fiber spaces andMordell's conjecture over function fields, Publ. Res. Inst. Math. Sci. (1) 21(1985), 27–46.Google Scholar
[No 2] Noguchi, J., Moduli spaces of holomorphic mappings into hyperbolically imbedded complex spaces and locally symmetric spaces, Invent. Math. 93(1988), 15–34.Google Scholar
[T] Ta, A.D.ĭmanov, On the extension of continuous mappings of topological spaces, (Russian) Mat. Sb. 31(1952), 459–462.Google Scholar