We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We introduce a relaxed version of the metric definition of quasiconformality that is natural also for mappings of low regularity, including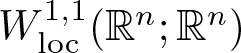 
$W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$-mappings. Then we show on the plane that this relaxed definition can be used to prove Sobolev regularity, and that these ‘finely quasiconformal’ mappings are in fact quasiconformal.
