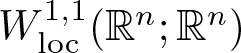1. Introduction
A homeomorphism ![]() $f\colon {\mathbb R}^n\to{\mathbb R}^n$ is said to be quasiconformal if
$f\colon {\mathbb R}^n\to{\mathbb R}^n$ is said to be quasiconformal if ![]() $K_f(x)\le K \lt \infty$ for all
$K_f(x)\le K \lt \infty$ for all ![]() $x\in{\mathbb R}^n$, where
$x\in{\mathbb R}^n$, where
 \begin{align*}
K_f(x):=\limsup_{r\to 0}\left(\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}\right)^{1/(n-1)}.
\end{align*}
\begin{align*}
K_f(x):=\limsup_{r\to 0}\left(\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}\right)^{1/(n-1)}.
\end{align*} We always consider ![]() $n\ge 2$, and we use
$n\ge 2$, and we use ![]() $|\cdot|$ for the Euclidean norm as well as for the Lebesgue measure. There are several equivalent definitions of quasiconformality; the above is a ‘metric’ definition. As part of an ‘analytic definition’, it is known that quasiconformal mappings are in the Sobolev class
$|\cdot|$ for the Euclidean norm as well as for the Lebesgue measure. There are several equivalent definitions of quasiconformality; the above is a ‘metric’ definition. As part of an ‘analytic definition’, it is known that quasiconformal mappings are in the Sobolev class  $W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$.
$W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$.
There has been wide interest in showing that if quasiconformality is assumed in some relaxed sense, it follows that the mapping in question is in fact quasiconformal, or at least has some lower regularity, such as  $W^{1,1}_{\mathrm{loc}}$-regularity. For example, Koskela–Rogovin [Reference Koskela and Rogovin15, corollary 1.3] show that if
$W^{1,1}_{\mathrm{loc}}$-regularity. For example, Koskela–Rogovin [Reference Koskela and Rogovin15, corollary 1.3] show that if ![]() $f\colon {\mathbb R}^n\to{\mathbb R}^n$ is a homeomorphism,
$f\colon {\mathbb R}^n\to{\mathbb R}^n$ is a homeomorphism, ![]() $K_f\in L^1_{\mathrm{loc}}({\mathbb R}^n)$, and
$K_f\in L^1_{\mathrm{loc}}({\mathbb R}^n)$, and ![]() $K_f \lt \infty$ outside a set of σ-finite
$K_f \lt \infty$ outside a set of σ-finite ![]() $\mathcal H^{n-1}$-measure, then
$\mathcal H^{n-1}$-measure, then  $f\in W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$. Many results in the same vein have been proven starting from Gehring [Reference Gehring8, Reference Gehring9], see also Balogh–Koskela [Reference Balogh and Koskela2], Fang [Reference Fang7], Heinonen–Koskela–Shanmugalingam–Tyson [Reference Heinonen, Koskela, Shanmugalingam and Tyson10], Kallunki–Koskela [Reference Kallunki and Koskela12], and Margulis–Mostow [Reference Margulis and Mostow20]. Several works study specifically the issue of
$f\in W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$. Many results in the same vein have been proven starting from Gehring [Reference Gehring8, Reference Gehring9], see also Balogh–Koskela [Reference Balogh and Koskela2], Fang [Reference Fang7], Heinonen–Koskela–Shanmugalingam–Tyson [Reference Heinonen, Koskela, Shanmugalingam and Tyson10], Kallunki–Koskela [Reference Kallunki and Koskela12], and Margulis–Mostow [Reference Margulis and Mostow20]. Several works study specifically the issue of  $W^{1,1}_{\mathrm{loc}}$-regularity, see Balogh–Koskela–Rogovin [Reference Balogh, Koskela and Rogovin3], Kallunki–Martio [Reference Kallunki and Martio13], and Williams [Reference Williams22].
$W^{1,1}_{\mathrm{loc}}$-regularity, see Balogh–Koskela–Rogovin [Reference Balogh, Koskela and Rogovin3], Kallunki–Martio [Reference Kallunki and Martio13], and Williams [Reference Williams22].
The quantity  $K_f^{n-1}$ can be essentially thought of as ‘
$K_f^{n-1}$ can be essentially thought of as ‘![]() $|\nabla f|^n$ divided by the Jacobian determinant’. Indeed, for a quasiconformal mapping
$|\nabla f|^n$ divided by the Jacobian determinant’. Indeed, for a quasiconformal mapping ![]() $f\colon {\mathbb R}^n\to{\mathbb R}^n$, we know that
$f\colon {\mathbb R}^n\to{\mathbb R}^n$, we know that
 \begin{align}
K_f(x)^{n-1}|\det \nabla f(x)|
= \frac{2^n}{\omega_n}\Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in {\mathbb R}^n,
\end{align}
\begin{align}
K_f(x)^{n-1}|\det \nabla f(x)|
= \frac{2^n}{\omega_n}\Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in {\mathbb R}^n,
\end{align} where ωn is the Lebesgue measure of the unit ball, ![]() $\Vert \cdot\Vert$ is the maximum norm, and
$\Vert \cdot\Vert$ is the maximum norm, and ![]() $\nabla f$ can be understood to be either the classical gradient or the weak gradient. With the latter interpretation, all of the quantities in (1.1) make sense also for mappings of lower Sobolev regularity, but the equality can fail already for
$\nabla f$ can be understood to be either the classical gradient or the weak gradient. With the latter interpretation, all of the quantities in (1.1) make sense also for mappings of lower Sobolev regularity, but the equality can fail already for  $W_{\mathrm{loc}}^{1,n}$-mappings—let alone
$W_{\mathrm{loc}}^{1,n}$-mappings—let alone  $W_{\mathrm{loc}}^{1,1}$-mappings—since for them
$W_{\mathrm{loc}}^{1,1}$-mappings—since for them ![]() $\operatorname{diam} f(B(x,r))$ can easily be
$\operatorname{diam} f(B(x,r))$ can easily be ![]() $\infty$ for every
$\infty$ for every ![]() $x\in {\mathbb R}^n$ and r > 0; see example 3.1. The problem is that the quantity Kf is very sensitive to oscillations and essentially tailored to mappings f that have better than
$x\in {\mathbb R}^n$ and r > 0; see example 3.1. The problem is that the quantity Kf is very sensitive to oscillations and essentially tailored to mappings f that have better than  $W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$-regularity. We wish to find a quantity that corresponds to ‘
$W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$-regularity. We wish to find a quantity that corresponds to ‘![]() $|\nabla f|^n$ divided by the Jacobian determinant’ in the case of
$|\nabla f|^n$ divided by the Jacobian determinant’ in the case of  $W^{1,1}_{\mathrm{loc}}$-mappings. Hence we define the relaxed quantities
$W^{1,1}_{\mathrm{loc}}$-mappings. Hence we define the relaxed quantities
 \begin{align*}
K_{f,U}(x,r):=\left(\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|f(B(x,r))|}\right)^{1/(n-1)}
\quad\textrm{and}\quad
K_f^{\mathrm{fine}}(x):=\inf\limsup_{r\to 0}K_{f,U}(x,r),
\end{align*}
\begin{align*}
K_{f,U}(x,r):=\left(\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|f(B(x,r))|}\right)^{1/(n-1)}
\quad\textrm{and}\quad
K_f^{\mathrm{fine}}(x):=\inf\limsup_{r\to 0}K_{f,U}(x,r),
\end{align*} where the infimum is taken over 1-finely open sets ![]() $U\ni x$; we give definitions in §2. In the following analog of (1.1),
$U\ni x$; we give definitions in §2. In the following analog of (1.1), ![]() $f^*$ is the so-called precise representative of f.
$f^*$ is the so-called precise representative of f.
Theorem 1.2. For every  $f\in W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$, we have
$f\in W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$, we have
 \begin{align*}
K_{f^*}^{\mathrm{fine}}(x)^{n-1}|\det \nabla f(x)|
\le \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in {\mathbb R}^n,
\end{align*}
\begin{align*}
K_{f^*}^{\mathrm{fine}}(x)^{n-1}|\det \nabla f(x)|
\le \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in {\mathbb R}^n,
\end{align*} with the interpretation ![]() $\infty\times 0=0$ if
$\infty\times 0=0$ if ![]() $\det \nabla f(x)=0$.
$\det \nabla f(x)=0$.
This shows that  $K_{f}^{\mathrm{fine}}$ is generally much smaller than Kf. On the other hand, the mapping we give in the aforementioned example 3.1 is by no means a homeomorphism. Thus one can ask: for a homeomorphism f, are conditions on
$K_{f}^{\mathrm{fine}}$ is generally much smaller than Kf. On the other hand, the mapping we give in the aforementioned example 3.1 is by no means a homeomorphism. Thus one can ask: for a homeomorphism f, are conditions on  $K_f^{\mathrm{fine}}$ enough to prove Sobolev regularity, or even quasiconformality? Our main result is the following analog on the plane of the aforementioned Koskela–Rogovin [Reference Koskela and Rogovin15] and of other similar results.
$K_f^{\mathrm{fine}}$ enough to prove Sobolev regularity, or even quasiconformality? Our main result is the following analog on the plane of the aforementioned Koskela–Rogovin [Reference Koskela and Rogovin15] and of other similar results.
Theorem 1.3. Let ![]() $f\colon {\mathbb R}^2\to {\mathbb R}^2$ be a homeomorphism. Let
$f\colon {\mathbb R}^2\to {\mathbb R}^2$ be a homeomorphism. Let ![]() $1\le p\le 2$. Suppose
$1\le p\le 2$. Suppose  $K_f^{\mathrm{fine}}\in L^{p^*/2}_{\mathrm{loc}}({\mathbb R}^2)$ and
$K_f^{\mathrm{fine}}\in L^{p^*/2}_{\mathrm{loc}}({\mathbb R}^2)$ and  $K_f^{\mathrm{fine}} \lt \infty$ outside a set E of σ-finite
$K_f^{\mathrm{fine}} \lt \infty$ outside a set E of σ-finite ![]() $\mathcal H^{1}$-measure. Then
$\mathcal H^{1}$-measure. Then  $f\in W_{\mathrm{loc}}^{1,p}({\mathbb R}^2;{\mathbb R}^2)$, and in the case p = 2 we obtain that f is quasiconformal and that
$f\in W_{\mathrm{loc}}^{1,p}({\mathbb R}^2;{\mathbb R}^2)$, and in the case p = 2 we obtain that f is quasiconformal and that  $K_f^{\mathrm{fine}}(x)=K_f(x)$ for a.e.
$K_f^{\mathrm{fine}}(x)=K_f(x)$ for a.e. ![]() $x\in{\mathbb R}^2$.
$x\in{\mathbb R}^2$.
Here ![]() $p^*=2p/(2-p)$ when
$p^*=2p/(2-p)$ when ![]() $1\le p \lt 2$, and
$1\le p \lt 2$, and ![]() $p^*=\infty$ when p = 2. In the case
$p^*=\infty$ when p = 2. In the case ![]() $1\le p \lt 2$, this theorem can be viewed as a statement about ‘finely quasiconformal’ mappings of low regularity. The condition on the size of the exceptional set E is known to be quite sharp, as noted, e.g., in remark 1.9 of Williams [Reference Williams22]; the same is true in our setting since the set where
$1\le p \lt 2$, this theorem can be viewed as a statement about ‘finely quasiconformal’ mappings of low regularity. The condition on the size of the exceptional set E is known to be quite sharp, as noted, e.g., in remark 1.9 of Williams [Reference Williams22]; the same is true in our setting since the set where  $K_f^{\mathrm{fine}}=\infty$ is of course smaller than the set where
$K_f^{\mathrm{fine}}=\infty$ is of course smaller than the set where ![]() $K_f=\infty$. In the case p = 2, we get the following corollary saying that ‘finely quasiconformal’ mappings are in fact quasiconformal.
$K_f=\infty$. In the case p = 2, we get the following corollary saying that ‘finely quasiconformal’ mappings are in fact quasiconformal.
Corollary 1.4. Let ![]() $f\colon {\mathbb R}^2\to {\mathbb R}^2$ be a homeomorphism and suppose that
$f\colon {\mathbb R}^2\to {\mathbb R}^2$ be a homeomorphism and suppose that  $K_f^{\mathrm{fine}}(x)\le K \lt \infty$ for every
$K_f^{\mathrm{fine}}(x)\le K \lt \infty$ for every ![]() $x\in {\mathbb R}^2$. Then f is quasiconformal.
$x\in {\mathbb R}^2$. Then f is quasiconformal.
2. Preliminaries
Our definitions and notation are standard, and the reader may consult, e.g., the monograph Evans–Gariepy [Reference Evans and Gariepy6] for more background. We will work in the Euclidean space ![]() ${\mathbb R}^n$ with
${\mathbb R}^n$ with ![]() $n\ge 2$. We denote the n-dimensional Lebesgue outer measure by
$n\ge 2$. We denote the n-dimensional Lebesgue outer measure by ![]() $\mathcal L^n$. We denote the s-dimensional Hausdorff content by
$\mathcal L^n$. We denote the s-dimensional Hausdorff content by ![]() $\mathcal H_{R}^{s}$ and the Hausdorff measure by
$\mathcal H_{R}^{s}$ and the Hausdorff measure by ![]() $\mathcal H^{s}$, with
$\mathcal H^{s}$, with ![]() $0 \lt R\le \infty$ and
$0 \lt R\le \infty$ and ![]() $0\le s\le n$. If a property holds outside a set of Lebesgue measure zero, we say that it holds almost everywhere, or ‘a.e.’.
$0\le s\le n$. If a property holds outside a set of Lebesgue measure zero, we say that it holds almost everywhere, or ‘a.e.’.
We denote the characteristic function of a set ![]() $A\subset{\mathbb R}^n$ by
$A\subset{\mathbb R}^n$ by ![]() $\chi_A\colon {\mathbb R}^n\to \{0,1\}$. We denote by
$\chi_A\colon {\mathbb R}^n\to \{0,1\}$. We denote by ![]() $|v|$ the Euclidean norm of
$|v|$ the Euclidean norm of ![]() $v\in {\mathbb R}^n$, and we also write
$v\in {\mathbb R}^n$, and we also write ![]() $|A|:=\mathcal L^n(A)$ for a set
$|A|:=\mathcal L^n(A)$ for a set ![]() $A\subset {\mathbb R}^n$. We write
$A\subset {\mathbb R}^n$. We write ![]() $B(x,r)$ for an open ball in
$B(x,r)$ for an open ball in ![]() ${\mathbb R}^n$ with centre
${\mathbb R}^n$ with centre ![]() $x\in {\mathbb R}^n$ and radius r > 0, that is,
$x\in {\mathbb R}^n$ and radius r > 0, that is, ![]() $B(x,r)=\{y \in {\mathbb R}^n \colon |y-x| \lt r\}$. We will sometimes use the notation
$B(x,r)=\{y \in {\mathbb R}^n \colon |y-x| \lt r\}$. We will sometimes use the notation ![]() $2B(x,r):=B(x,2r)$. For matrices
$2B(x,r):=B(x,2r)$. For matrices ![]() $A\in {\mathbb R}^{n\times n}$, we consider the Euclidean norm
$A\in {\mathbb R}^{n\times n}$, we consider the Euclidean norm ![]() $|A|$ as well as the maximum norm
$|A|$ as well as the maximum norm
 \begin{align*}
\Vert A\Vert:=\max_{v\in{\mathbb R}^n,\,|v|=1}|Av|.
\end{align*}
\begin{align*}
\Vert A\Vert:=\max_{v\in{\mathbb R}^n,\,|v|=1}|Av|.
\end{align*} By ‘measurable’, we mean ![]() $\mathcal L^n$-measurable, unless otherwise specified. If a function u is in
$\mathcal L^n$-measurable, unless otherwise specified. If a function u is in ![]() $L^1(D)$ for some measurable set
$L^1(D)$ for some measurable set ![]() $D \subset {\mathbb R}^n$ of nonzero and finite Lebesgue measure, we write
$D \subset {\mathbb R}^n$ of nonzero and finite Lebesgue measure, we write
 \begin{align*}
u_D:= -\!\!\!\!\!\!\int_D u(y) \,d\mathcal L^n(y) {:=} \frac{1}{\mathcal L^n(D)} \int_D u(y) \,d\mathcal L^n(y)
\end{align*}
\begin{align*}
u_D:= -\!\!\!\!\!\!\int_D u(y) \,d\mathcal L^n(y) {:=} \frac{1}{\mathcal L^n(D)} \int_D u(y) \,d\mathcal L^n(y)
\end{align*}for its mean value in D.
We will always denote by ![]() $\Omega\subset{\mathbb R}^n$ an open set, and we consider
$\Omega\subset{\mathbb R}^n$ an open set, and we consider ![]() $1\le p \lt \infty$. Let
$1\le p \lt \infty$. Let ![]() $l\in{\mathbb N}$. The Sobolev space
$l\in{\mathbb N}$. The Sobolev space ![]() $W^{1,p}(\Omega;{\mathbb R}^l)$ consists of mappings
$W^{1,p}(\Omega;{\mathbb R}^l)$ consists of mappings ![]() $f\in L^p(\Omega;{\mathbb R}^l)$ whose first weak partial derivatives
$f\in L^p(\Omega;{\mathbb R}^l)$ whose first weak partial derivatives ![]() $\partial f_j/\partial x_k$,
$\partial f_j/\partial x_k$, ![]() $j=1,\ldots,l$,
$j=1,\ldots,l$, ![]() $k=1,\ldots,n$, belong to
$k=1,\ldots,n$, belong to ![]() $L^p(\Omega)$. We will only consider l = 1 or l = n. The weak partial derivatives form the matrix
$L^p(\Omega)$. We will only consider l = 1 or l = n. The weak partial derivatives form the matrix ![]() $(\nabla f)_{jk}$. The Dirichlet space
$(\nabla f)_{jk}$. The Dirichlet space ![]() $D^{p}(\Omega;{\mathbb R}^l)$ is defined in the same way, except that the integrability requirement for the mapping itself is relaxed to
$D^{p}(\Omega;{\mathbb R}^l)$ is defined in the same way, except that the integrability requirement for the mapping itself is relaxed to ![]() $f\in L_{\mathrm{loc}}^1(\Omega;{\mathbb R}^l)$. The Sobolev norm is
$f\in L_{\mathrm{loc}}^1(\Omega;{\mathbb R}^l)$. The Sobolev norm is
 \begin{align*}
\Vert f\Vert_{W^{1,p}(\Omega;{\mathbb R}^l)}
:=\Vert f\Vert_{L^p(\Omega;{\mathbb R}^l)}+\Vert \nabla f\Vert_{L^p(\Omega;{\mathbb R}^{l\times n})},
\end{align*}
\begin{align*}
\Vert f\Vert_{W^{1,p}(\Omega;{\mathbb R}^l)}
:=\Vert f\Vert_{L^p(\Omega;{\mathbb R}^l)}+\Vert \nabla f\Vert_{L^p(\Omega;{\mathbb R}^{l\times n})},
\end{align*}where the Lp norms are defined with respect to the Euclidean norm.
Consider a homeomorphism ![]() $f\colon \Omega\to \Omega'$, with
$f\colon \Omega\to \Omega'$, with ![]() $\Omega,\Omega'\subset {\mathbb R}^n$ open. In addition to the Jacobian determinant
$\Omega,\Omega'\subset {\mathbb R}^n$ open. In addition to the Jacobian determinant ![]() $\det \nabla f(x)$, we also define the Jacobian
$\det \nabla f(x)$, we also define the Jacobian
 \begin{align}
J_f(x):=\limsup_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|},\quad x\in\Omega.
\end{align}
\begin{align}
J_f(x):=\limsup_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|},\quad x\in\Omega.
\end{align}Note that Jf is the density of the pullback measure
By well-known results on densities, see e.g. [Reference Evans and Gariepy6, p. 42], we know the following: ![]() $J_f(x)$ exists as a limit for a.e.
$J_f(x)$ exists as a limit for a.e. ![]() $x\in\Omega$, is a Borel function, and
$x\in\Omega$, is a Borel function, and
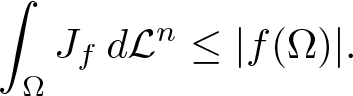 \begin{align}
\int_{\Omega}J_f\,d\mathcal L^n\le |f(\Omega)|.
\end{align}
\begin{align}
\int_{\Omega}J_f\,d\mathcal L^n\le |f(\Omega)|.
\end{align} Equality holds if f is absolutely continuous in measure, that is, if ![]() $|A|=0$ implies
$|A|=0$ implies ![]() $|f(A)|=0$. We will use the following ‘analytic’ definition of quasiconformality. For the equivalence of different definitions of quasiconformality, including the metric definition used in the introduction, see e.g. [Reference Heinonen, Koskela, Shanmugalingam and Tyson10, theorem 9.8].
$|f(A)|=0$. We will use the following ‘analytic’ definition of quasiconformality. For the equivalence of different definitions of quasiconformality, including the metric definition used in the introduction, see e.g. [Reference Heinonen, Koskela, Shanmugalingam and Tyson10, theorem 9.8].
Definition 2.3. Let ![]() $\Omega,\Omega'\subset {\mathbb R}^n$ be open sets. A homeomorphism
$\Omega,\Omega'\subset {\mathbb R}^n$ be open sets. A homeomorphism  $f\in W_{\mathrm{loc}}^{1,n}(\Omega;\Omega')$ is said to be quasiconformal if
$f\in W_{\mathrm{loc}}^{1,n}(\Omega;\Omega')$ is said to be quasiconformal if
for some constant ![]() $K \lt \infty$.
$K \lt \infty$.
Here we understand ![]() $\nabla f$ to be the weak gradient. However, as a homeomorphism, f is locally monotone, and combining this with the fact that
$\nabla f$ to be the weak gradient. However, as a homeomorphism, f is locally monotone, and combining this with the fact that  $f\in W_{\mathrm{loc}}^{1,n}(\Omega;\Omega')$, by, e.g., Malý [Reference Malý18, theorems 3.3 and 4.3] we know that f is differentiable a.e. Moreover, by [Reference Malý and Martio19, corollary B] and [Reference Malý18, theorem 3.4], such f is absolutely continuous in measure and satisfies the area formula, implying that
$f\in W_{\mathrm{loc}}^{1,n}(\Omega;\Omega')$, by, e.g., Malý [Reference Malý18, theorems 3.3 and 4.3] we know that f is differentiable a.e. Moreover, by [Reference Malý and Martio19, corollary B] and [Reference Malý18, theorem 3.4], such f is absolutely continuous in measure and satisfies the area formula, implying that
 \begin{align*}
\int_W J_f\,d\mathcal L^n=|f(W)|
=\int_W |\det \nabla f|\,d\mathcal L^n
\end{align*}
\begin{align*}
\int_W J_f\,d\mathcal L^n=|f(W)|
=\int_W |\det \nabla f|\,d\mathcal L^n
\end{align*} for every open ![]() $W\subset \Omega$, and so
$W\subset \Omega$, and so ![]() $|\det \nabla f|=J_f$ a.e. in Ω. Thus in (2.4), we could equivalently replace
$|\det \nabla f|=J_f$ a.e. in Ω. Thus in (2.4), we could equivalently replace ![]() $|\det \nabla f|$ with Jf.
$|\det \nabla f|$ with Jf.
We will need the following Vitali–Carathéodory theorem; for a proof see e.g. [Reference Heinonen, Koskela, Shanmugalingam and Tyson11, p. 108].
Theorem 2.5. Let ![]() $\Omega\subset {\mathbb R}^n$ be open and let
$\Omega\subset {\mathbb R}^n$ be open and let ![]() $h\in L^1(\Omega)$ be nonnegative. Then there exists a sequence
$h\in L^1(\Omega)$ be nonnegative. Then there exists a sequence ![]() $\{h_i\}_{i=1}^{\infty}$ of lower semicontinuous functions on Ω such that
$\{h_i\}_{i=1}^{\infty}$ of lower semicontinuous functions on Ω such that ![]() $h\le h_{i+1}\le h_i$ for all
$h\le h_{i+1}\le h_i$ for all ![]() $i\in{\mathbb N}$, and
$i\in{\mathbb N}$, and ![]() $h_i\to h$ in
$h_i\to h$ in ![]() $L^1(\Omega)$.
$L^1(\Omega)$.
The theory of ![]() $\mathrm{BV}$ mappings that we present next can be found in the monograph Ambrosio–Fusco–Pallara [Reference Ambrosio, Fusco and Pallara1]. As before, let
$\mathrm{BV}$ mappings that we present next can be found in the monograph Ambrosio–Fusco–Pallara [Reference Ambrosio, Fusco and Pallara1]. As before, let ![]() $\Omega\subset{\mathbb R}^n$ be an open set. Let
$\Omega\subset{\mathbb R}^n$ be an open set. Let ![]() $l\in{\mathbb N}$. A mapping
$l\in{\mathbb N}$. A mapping ![]() $f\in L^1(\Omega;{\mathbb R}^l)$ is of bounded variation, denoted
$f\in L^1(\Omega;{\mathbb R}^l)$ is of bounded variation, denoted ![]() $f\in \mathrm{BV}(\Omega;{\mathbb R}^l)$, if its weak derivative is an
$f\in \mathrm{BV}(\Omega;{\mathbb R}^l)$, if its weak derivative is an ![]() ${\mathbb R}^{l\times n}$-valued Radon measure with finite total variation. This means that there exists a (unique) Radon measure Df such that for all
${\mathbb R}^{l\times n}$-valued Radon measure with finite total variation. This means that there exists a (unique) Radon measure Df such that for all ![]() $\varphi\in C_c^1(\Omega)$, the integration-by-parts formula
$\varphi\in C_c^1(\Omega)$, the integration-by-parts formula
 \begin{align*}
\int_{\Omega}f_j\frac{\partial\varphi}{\partial x_k}\,d\mathcal L^n
=-\int_{\Omega}\varphi\,d(Df_j)_k,\quad j=1,\ldots,l,\ k=1,\ldots,n,
\end{align*}
\begin{align*}
\int_{\Omega}f_j\frac{\partial\varphi}{\partial x_k}\,d\mathcal L^n
=-\int_{\Omega}\varphi\,d(Df_j)_k,\quad j=1,\ldots,l,\ k=1,\ldots,n,
\end{align*} holds. The total variation of Df is denoted by ![]() $|Df|$. The BV norm is defined by
$|Df|$. The BV norm is defined by
 \begin{align*}
\Vert f\Vert_{\mathrm{BV}(\Omega)}:=\Vert f\Vert_{L^1(\Omega)}+|Df|(\Omega).
\end{align*}
\begin{align*}
\Vert f\Vert_{\mathrm{BV}(\Omega)}:=\Vert f\Vert_{L^1(\Omega)}+|Df|(\Omega).
\end{align*} We denote by ![]() $\nabla f$ the density of the absolutely continuous part of Df. If we do not know a priori that a mapping
$\nabla f$ the density of the absolutely continuous part of Df. If we do not know a priori that a mapping ![]() $f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^l)$ is a BV mapping, we consider
$f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^l)$ is a BV mapping, we consider
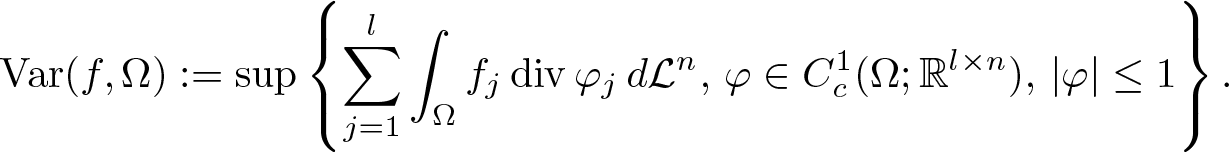 \begin{align}
\operatorname{Var}(f,\Omega):=\sup\left\{\sum_{j=1}^{l}\int_{\Omega}f_j\operatorname{div}\varphi_j\,d\mathcal L^n,\,\varphi\in C_c^{1}(\Omega;{\mathbb R}^{l\times n}),
\,|\varphi|\le 1\right\}.
\end{align}
\begin{align}
\operatorname{Var}(f,\Omega):=\sup\left\{\sum_{j=1}^{l}\int_{\Omega}f_j\operatorname{div}\varphi_j\,d\mathcal L^n,\,\varphi\in C_c^{1}(\Omega;{\mathbb R}^{l\times n}),
\,|\varphi|\le 1\right\}.
\end{align} If ![]() $\operatorname{Var}(f,\Omega) \lt \infty$, then the
$\operatorname{Var}(f,\Omega) \lt \infty$, then the ![]() ${\mathbb R}^{l\times n}$-valued Radon measure Df exists and
${\mathbb R}^{l\times n}$-valued Radon measure Df exists and ![]() $\operatorname{Var}(f,\Omega)=|Df|(\Omega)$ by the Riesz representation theorem, and
$\operatorname{Var}(f,\Omega)=|Df|(\Omega)$ by the Riesz representation theorem, and ![]() $f\in\mathrm{BV}(\Omega)$ provided that
$f\in\mathrm{BV}(\Omega)$ provided that ![]() $f\in L^1(\Omega;{\mathbb R}^l)$. If
$f\in L^1(\Omega;{\mathbb R}^l)$. If ![]() $E\subset{\mathbb R}^n$ with
$E\subset{\mathbb R}^n$ with ![]() $\operatorname{Var}(\chi_E,{\mathbb R}^n) \lt \infty$, we say that E is a set of finite perimeter.
$\operatorname{Var}(\chi_E,{\mathbb R}^n) \lt \infty$, we say that E is a set of finite perimeter.
The coarea formula states that for a function ![]() $u\in \mathrm{BV}(\Omega)$, we have
$u\in \mathrm{BV}(\Omega)$, we have
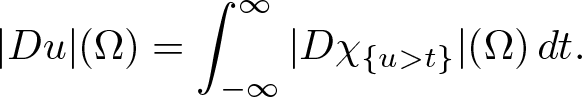 \begin{align}
|Du|(\Omega)=\int_{-\infty}^{\infty}|D\chi_{\{u \gt t\}}|(\Omega)\,dt.
\end{align}
\begin{align}
|Du|(\Omega)=\int_{-\infty}^{\infty}|D\chi_{\{u \gt t\}}|(\Omega)\,dt.
\end{align} Here we abbreviate ![]() $\{u \gt t\}:=\{x\in \Omega\colon u(x) \gt t\}$.
$\{u \gt t\}:=\{x\in \Omega\colon u(x) \gt t\}$.
The relative isoperimetric inequality states that for every set of finite perimeter ![]() $E\subset {\mathbb R}^n$ and every ball
$E\subset {\mathbb R}^n$ and every ball ![]() $B(x,r)$, we have
$B(x,r)$, we have
where the constant ![]() $C_I\ge 1$ only depends on n. The following relative isoperimetric inequality holds on the plane: for every set of finite perimeter
$C_I\ge 1$ only depends on n. The following relative isoperimetric inequality holds on the plane: for every set of finite perimeter ![]() $E\subset {\mathbb R}^2$ and every disk
$E\subset {\mathbb R}^2$ and every disk ![]() $B(x,r)$, we have
$B(x,r)$, we have
For ![]() $f\in L^1_{\mathrm{loc}}(\Omega)$, we define the precise representative by
$f\in L^1_{\mathrm{loc}}(\Omega)$, we define the precise representative by
 \begin{align}
f^*(x):=\limsup_{r\to 0} -\!\!\!\!\!\!\int_{{B(x,r)}} f\,d\mathcal L^n,\quad x\in \Omega.
\end{align}
\begin{align}
f^*(x):=\limsup_{r\to 0} -\!\!\!\!\!\!\int_{{B(x,r)}} f\,d\mathcal L^n,\quad x\in \Omega.
\end{align} For ![]() $f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we let
$f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we let ![]() $f^*(x):=(f_1^*(x),\ldots,f_n^*(x))$.
$f^*(x):=(f_1^*(x),\ldots,f_n^*(x))$.
For basic results in the one-dimensional case n = 1, see [Reference Ambrosio, Fusco and Pallara1, Section 3.2]. If ![]() $\Omega\subset {\mathbb R}$ is an open interval, we define the pointwise variation of
$\Omega\subset {\mathbb R}$ is an open interval, we define the pointwise variation of ![]() $f\colon \Omega\to {\mathbb R}^n$ by
$f\colon \Omega\to {\mathbb R}^n$ by
 \begin{align}
\operatorname{pV}(f,\Omega):=\sup \sum_{j=1}^{N-1} |f(x_{j})-f(x_{j+1})|,
\end{align}
\begin{align}
\operatorname{pV}(f,\Omega):=\sup \sum_{j=1}^{N-1} |f(x_{j})-f(x_{j+1})|,
\end{align} where the supremum is taken over all collections of points ![]() $x_1 \lt \cdots \lt x_N$ in Ω. For a general open
$x_1 \lt \cdots \lt x_N$ in Ω. For a general open ![]() $\Omega\subset {\mathbb R}$, we define
$\Omega\subset {\mathbb R}$, we define ![]() $\operatorname{pV}(f,\Omega)$ to be
$\operatorname{pV}(f,\Omega)$ to be ![]() $\sum \operatorname{pV}(f,I)$, where the sum runs over all connected components I of Ω. For every pointwise defined
$\sum \operatorname{pV}(f,I)$, where the sum runs over all connected components I of Ω. For every pointwise defined ![]() $f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we have
$f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we have ![]() $\operatorname{Var}(f,\Omega)\le \operatorname{pV}(f,\Omega)$.
$\operatorname{Var}(f,\Omega)\le \operatorname{pV}(f,\Omega)$.
Denote by ![]() $\pi_n\colon{\mathbb R}^n\to {\mathbb R}^{n-1}$ the orthogonal projection onto
$\pi_n\colon{\mathbb R}^n\to {\mathbb R}^{n-1}$ the orthogonal projection onto ![]() ${\mathbb R}^{n-1}$: for
${\mathbb R}^{n-1}$: for ![]() $x=(x_1,\ldots,x_n)\in{\mathbb R}^n$,
$x=(x_1,\ldots,x_n)\in{\mathbb R}^n$,
For ![]() $z\in\pi_n(\Omega)$, we denote the slices of an open set
$z\in\pi_n(\Omega)$, we denote the slices of an open set ![]() $\Omega\subset{\mathbb R}^n$ by
$\Omega\subset{\mathbb R}^n$ by
We also denote ![]() $f_z(t){:=} f(z,t)$ for
$f_z(t){:=} f(z,t)$ for ![]() $z\in\pi_n(\Omega)$ and
$z\in\pi_n(\Omega)$ and ![]() $t\in \Omega_z$. For any continuous
$t\in \Omega_z$. For any continuous ![]() $f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we know that
$f\in L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, we know that ![]() $\operatorname{Var}(f,\Omega)$ is at most the sum of
$\operatorname{Var}(f,\Omega)$ is at most the sum of
 \begin{align}
\int_{\pi_n(\Omega)}\operatorname{pV}(f_z,\Omega_z)\,d\mathcal L^{n-1}(z)
\end{align}
\begin{align}
\int_{\pi_n(\Omega)}\operatorname{pV}(f_z,\Omega_z)\,d\mathcal L^{n-1}(z)
\end{align}and the analogous quantities for the other n − 1 coordinate directions, see [Reference Ambrosio, Fusco and Pallara1, theorem 3.103].
The (Sobolev) 1-capacity of a set ![]() $A\subset {\mathbb R}^n$ is defined by
$A\subset {\mathbb R}^n$ is defined by
 \begin{align*}
\operatorname{Cap}_1(A):=\inf \Vert u\Vert_{W^{1,1}({\mathbb R}^n)},
\end{align*}
\begin{align*}
\operatorname{Cap}_1(A):=\inf \Vert u\Vert_{W^{1,1}({\mathbb R}^n)},
\end{align*} where the infimum is taken over Sobolev functions ![]() $u\in W^{1,1}({\mathbb R}^n)$ satisfying
$u\in W^{1,1}({\mathbb R}^n)$ satisfying ![]() $u\ge 1$ in a neighbourhood of A.
$u\ge 1$ in a neighbourhood of A.
Given sets ![]() $A\subset W\subset {\mathbb R}^n$, where W is open, the relative p-capacity is defined by
$A\subset W\subset {\mathbb R}^n$, where W is open, the relative p-capacity is defined by
 \begin{align*}
\operatorname{cap}_1(A,W):=\inf \int_{W}|\nabla u|\,d\mathcal L^n,
\end{align*}
\begin{align*}
\operatorname{cap}_1(A,W):=\inf \int_{W}|\nabla u|\,d\mathcal L^n,
\end{align*} where the infimum is taken over functions  $u\in W_0^{1,1}(W)$ satisfying
$u\in W_0^{1,1}(W)$ satisfying ![]() $u\ge 1$ in a neighbourhood of A. The class
$u\ge 1$ in a neighbourhood of A. The class  $W_0^{1,1}(W)$ is the closure of
$W_0^{1,1}(W)$ is the closure of ![]() $C^1_c(W)$ in the
$C^1_c(W)$ in the ![]() $W^{1,p}({\mathbb R}^n)$-norm.
$W^{1,p}({\mathbb R}^n)$-norm.
By [Reference Carriero, Dal Maso, Leaci and Pascali5, theorem 3.3], given a function ![]() $u\in\mathrm{BV}(\Omega)$, there is a sequence
$u\in\mathrm{BV}(\Omega)$, there is a sequence ![]() $\{u_j\}_{j=1}^{\infty}$ of functions in
$\{u_j\}_{j=1}^{\infty}$ of functions in ![]() $W^{1,1}(\Omega)$ such that
$W^{1,1}(\Omega)$ such that
 \begin{align}
u_j\to u \ \textrm{in }L^1(\Omega),\quad |Du_j|(\Omega)\to |Du|(\Omega),\
\textrm{and }\ u^{\vee}_j(x)\ge u^{\vee}(x)\ \textrm{for }\mathcal H^{n-1}\textrm{-a.e. }x\in\Omega.
\end{align}
\begin{align}
u_j\to u \ \textrm{in }L^1(\Omega),\quad |Du_j|(\Omega)\to |Du|(\Omega),\
\textrm{and }\ u^{\vee}_j(x)\ge u^{\vee}(x)\ \textrm{for }\mathcal H^{n-1}\textrm{-a.e. }x\in\Omega.
\end{align} If ![]() $B(x,r)$ is a ball with
$B(x,r)$ is a ball with ![]() $0 \lt r\le 1$, and F is a measurable set with
$0 \lt r\le 1$, and F is a measurable set with  $\mathcal L^n(F\cap B(x,r))\le \tfrac 12 \mathcal L^n(B(x,r))$ and
$\mathcal L^n(F\cap B(x,r))\le \tfrac 12 \mathcal L^n(B(x,r))$ and ![]() $|D\chi_F|(B(x,r)) \lt \infty$, then by combining, e.g., theorem 5.6 and theorem 5.15(iii) of [Reference Evans and Gariepy6], we get
$|D\chi_F|(B(x,r)) \lt \infty$, then by combining, e.g., theorem 5.6 and theorem 5.15(iii) of [Reference Evans and Gariepy6], we get
for some constant C depending only on ![]() $n,r$. On the other hand, by the relative isoperimetric inequality (2.8), we have
$n,r$. On the other hand, by the relative isoperimetric inequality (2.8), we have
 \begin{align*}
\Vert \chi_F\Vert_{\mathrm{BV}(B(x,r))}
= \mathcal L^n(F\cap B(x,r))+|D\chi_F|(B(x,r))
&\le (C_I r+1)|D\chi_F|(B(x,r))\\
&\le 2C_I |D\chi_F|(B(x,r)),
\end{align*}
\begin{align*}
\Vert \chi_F\Vert_{\mathrm{BV}(B(x,r))}
= \mathcal L^n(F\cap B(x,r))+|D\chi_F|(B(x,r))
&\le (C_I r+1)|D\chi_F|(B(x,r))\\
&\le 2C_I |D\chi_F|(B(x,r)),
\end{align*} since ![]() $r\le 1$ and
$r\le 1$ and ![]() $C_I\ge 1$. Combining these, we get
$C_I\ge 1$. Combining these, we get
and by a scaling argument we see that in fact C only depends on n, not on r.
By [Reference Björn and Björn4, proposition 6.16], we know that for a ball ![]() $B(x,r)$ and
$B(x,r)$ and ![]() $A\subset B(x,r)$, we have
$A\subset B(x,r)$, we have
 \begin{align}
\frac{\operatorname{Cap}_1(A)}{C'(1+r)}
\le \operatorname{cap}_1(A,B(x,2r)),
\end{align}
\begin{align}
\frac{\operatorname{Cap}_1(A)}{C'(1+r)}
\le \operatorname{cap}_1(A,B(x,2r)),
\end{align}where Cʹ is a constant depending only on n.
We denote ![]() $\omega_{n}:=|B(0,1)|$.
$\omega_{n}:=|B(0,1)|$.
Lemma 2.17. Suppose ![]() $x\in{\mathbb R}^n$,
$x\in{\mathbb R}^n$, ![]() $0 \lt r \lt 1$, and
$0 \lt r \lt 1$, and ![]() $A\subset B(x,r)$. Then we have
$A\subset B(x,r)$. Then we have
 \begin{align*}
\frac{\mathcal L^n(A)}{\mathcal L^n(B(x,r))}\le \frac{2C_I}{\omega_n}\frac{\operatorname{Cap}_1(A)}{r^{n-1}}
\quad\textrm{and}\quad
\operatorname{cap}_1(A,B(x,2r))\le C\operatorname{Cap}_1(A),
\end{align*}
\begin{align*}
\frac{\mathcal L^n(A)}{\mathcal L^n(B(x,r))}\le \frac{2C_I}{\omega_n}\frac{\operatorname{Cap}_1(A)}{r^{n-1}}
\quad\textrm{and}\quad
\operatorname{cap}_1(A,B(x,2r))\le C\operatorname{Cap}_1(A),
\end{align*}where CI is the constant in the relative isoperimetric inequality (2.8), and C is a constant depending only on n.
Proof. For both inequalities, we can assume that ![]() $\operatorname{Cap}_1(A) \lt \infty$. Let ɛ > 0. We can choose a function
$\operatorname{Cap}_1(A) \lt \infty$. Let ɛ > 0. We can choose a function ![]() $u\in W^{1,1}({\mathbb R}^n)$ such that
$u\in W^{1,1}({\mathbb R}^n)$ such that ![]() $u\ge 1$ in a neighbourhood of A, and
$u\ge 1$ in a neighbourhood of A, and
 \begin{align*}
\Vert u\Vert_{W^{1,1}({\mathbb R}^n)} \lt \operatorname{Cap}_1(A)+\varepsilon.
\end{align*}
\begin{align*}
\Vert u\Vert_{W^{1,1}({\mathbb R}^n)} \lt \operatorname{Cap}_1(A)+\varepsilon.
\end{align*} By the coarea formula (2.7), we then find ![]() $0 \lt t \lt 1$ such that
$0 \lt t \lt 1$ such that ![]() $\{u \gt t\}$ contains a neighbourhood of A and
$\{u \gt t\}$ contains a neighbourhood of A and
 \begin{align*}
| D\chi_{\{u \gt t\}}|({\mathbb R}^n)\le |Du|({\mathbb R}^n)\le \Vert u\Vert_{W^{1,1}({\mathbb R}^n)} \lt \operatorname{Cap}_1(A)+\varepsilon.
\end{align*}
\begin{align*}
| D\chi_{\{u \gt t\}}|({\mathbb R}^n)\le |Du|({\mathbb R}^n)\le \Vert u\Vert_{W^{1,1}({\mathbb R}^n)} \lt \operatorname{Cap}_1(A)+\varepsilon.
\end{align*} Denote ![]() $F:=\{u \gt t\}$.
$F:=\{u \gt t\}$.
Case 1: Suppose  $\mathcal L^n(F\cap B(x,r))\ge \tfrac 12 \mathcal L^n(B(x,r))$. We find
$\mathcal L^n(F\cap B(x,r))\ge \tfrac 12 \mathcal L^n(B(x,r))$. We find ![]() $R\ge r$ such that
$R\ge r$ such that  $\mathcal L^n(F\cap B(x,R))= \tfrac 12 \mathcal L^n(B(x,R))$. By the relative isoperimetric inequality (2.8), we have
$\mathcal L^n(F\cap B(x,R))= \tfrac 12 \mathcal L^n(B(x,R))$. By the relative isoperimetric inequality (2.8), we have
 \begin{align}
\begin{split}
\operatorname{Cap}_1(A)+\varepsilon \gt |D\chi_F|({\mathbb R}^n)
\ge |D\chi_F|(B(x,R))
&\ge C_I^{-1} \frac 12 R^{-1} \mathcal L^n(B(x,R))\\
&=\frac{\omega_n}{2C_I} R^{n-1}\\
&\ge\frac{\omega_n}{2C_I} r^{n-1}\\
&\ge \frac{\omega_n}{2C_I} r^{n-1}\frac{\mathcal L^n(F\cap B(x,r))}{\mathcal L^n(B(x,r))}\\
&\ge \frac{\omega_n}{2C_I} r^{n-1}\frac{\mathcal L^n(A)}{\mathcal L^n(B(x,r))}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\operatorname{Cap}_1(A)+\varepsilon \gt |D\chi_F|({\mathbb R}^n)
\ge |D\chi_F|(B(x,R))
&\ge C_I^{-1} \frac 12 R^{-1} \mathcal L^n(B(x,R))\\
&=\frac{\omega_n}{2C_I} R^{n-1}\\
&\ge\frac{\omega_n}{2C_I} r^{n-1}\\
&\ge \frac{\omega_n}{2C_I} r^{n-1}\frac{\mathcal L^n(F\cap B(x,r))}{\mathcal L^n(B(x,r))}\\
&\ge \frac{\omega_n}{2C_I} r^{n-1}\frac{\mathcal L^n(A)}{\mathcal L^n(B(x,r))}.
\end{split}
\end{align}Letting ɛ → 0, we get the first result. Defining the cut-off function
 \begin{align}
\eta(y):=\max\left\{0,1-\frac{1}{r}\operatorname{dist}(y,B(x, r))\right\},\quad y\in{\mathbb R}^n,
\end{align}
\begin{align}
\eta(y):=\max\left\{0,1-\frac{1}{r}\operatorname{dist}(y,B(x, r))\right\},\quad y\in{\mathbb R}^n,
\end{align} for which η = 1 in ![]() $B(x,r)$ and η = 0 in
$B(x,r)$ and η = 0 in ![]() ${\mathbb R}^n\setminus B(x,2r)$, we get
${\mathbb R}^n\setminus B(x,2r)$, we get
 \begin{align*}
\operatorname{cap}_1(A,B(x,2r))
\le \int_{{\mathbb R}^n} |\nabla \eta|\,d\mathcal L^n
\le \frac{\omega_n (2r)^n}{r}
\le 2^{n+1}C_I (\operatorname{Cap}_1(A)+\varepsilon)
\end{align*}
\begin{align*}
\operatorname{cap}_1(A,B(x,2r))
\le \int_{{\mathbb R}^n} |\nabla \eta|\,d\mathcal L^n
\le \frac{\omega_n (2r)^n}{r}
\le 2^{n+1}C_I (\operatorname{Cap}_1(A)+\varepsilon)
\end{align*} by the first three lines of (2.18). Letting ɛ → 0, we get the second result with ![]() $C=2^{n+1}C_I$.
$C=2^{n+1}C_I$.
Case 2: Suppose  $\mathcal L^n(F\cap B(x,r)) \lt \tfrac 12 \mathcal L^n(B(x,r))$. By the relative isoperimetric inequality,
$\mathcal L^n(F\cap B(x,r)) \lt \tfrac 12 \mathcal L^n(B(x,r))$. By the relative isoperimetric inequality,
 \begin{align*}
\operatorname{Cap}_1(A)+\varepsilon
\ge |D\chi_F|({\mathbb R}^n)
\ge |D\chi_F|(B(x,r))
&\ge \frac{1}{C_Ir}\mathcal L^n(F\cap B(x,r))\\
&\ge \frac{1}{C_Ir}\mathcal L^n(A)\\
&\ge \frac{\omega_n}{C_I}\mathcal L^n(A)\frac{r^{n-1}}{\mathcal L^n(B(x,r))}.
\end{align*}
\begin{align*}
\operatorname{Cap}_1(A)+\varepsilon
\ge |D\chi_F|({\mathbb R}^n)
\ge |D\chi_F|(B(x,r))
&\ge \frac{1}{C_Ir}\mathcal L^n(F\cap B(x,r))\\
&\ge \frac{1}{C_Ir}\mathcal L^n(A)\\
&\ge \frac{\omega_n}{C_I}\mathcal L^n(A)\frac{r^{n-1}}{\mathcal L^n(B(x,r))}.
\end{align*}Letting ɛ → 0, we get the first result.
By (2.15), we get
By (2.14), we find a sequence ![]() $\{u_j\}_{j=1}^{\infty}$ in
$\{u_j\}_{j=1}^{\infty}$ in ![]() $W^{1,1}({\mathbb R}^n)$ such that
$W^{1,1}({\mathbb R}^n)$ such that ![]() $u_j\to \chi_{B(x,r)\cap F}$ in
$u_j\to \chi_{B(x,r)\cap F}$ in ![]() $L^1({\mathbb R}^n)$,
$L^1({\mathbb R}^n)$, ![]() $|Du_j|({\mathbb R}^n)\to |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)$, and
$|Du_j|({\mathbb R}^n)\to |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)$, and ![]() $u_j\ge 1$ a.e. in a neighbourhood of A. Consider the cut-off function η from (2.19). We have
$u_j\ge 1$ a.e. in a neighbourhood of A. Consider the cut-off function η from (2.19). We have ![]() $u_j\eta \to \chi_{B(x,r)\cap F}$ in
$u_j\eta \to \chi_{B(x,r)\cap F}$ in ![]() $L^1({\mathbb R}^n)$,
$L^1({\mathbb R}^n)$, ![]() $|D(u_j \eta)|({\mathbb R}^n)\to |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)$, and
$|D(u_j \eta)|({\mathbb R}^n)\to |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)$, and ![]() $u_j\eta \ge 1$ a.e. in a neighbourhood of A. Thus
$u_j\eta \ge 1$ a.e. in a neighbourhood of A. Thus
 \begin{align*}
\operatorname{cap}_1(A,B(x,2r))
\le \liminf_{j\to\infty}\int_{{\mathbb R}^n}|\nabla (u_j \eta)|\,d\mathcal L^n
&= |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)\\
&\le C\operatorname{Cap}_1(A)+C\varepsilon\quad\textrm{by (2.20)}.
\end{align*}
\begin{align*}
\operatorname{cap}_1(A,B(x,2r))
\le \liminf_{j\to\infty}\int_{{\mathbb R}^n}|\nabla (u_j \eta)|\,d\mathcal L^n
&= |D\chi_{B(x,r)\cap F}|({\mathbb R}^n)\\
&\le C\operatorname{Cap}_1(A)+C\varepsilon\quad\textrm{by (2.20)}.
\end{align*}Letting ɛ → 0, we get the second result.
Definition 2.21. We say that ![]() $A\subset {\mathbb R}^n$ is 1-thin at the point
$A\subset {\mathbb R}^n$ is 1-thin at the point ![]() $x\in {\mathbb R}^n$ if
$x\in {\mathbb R}^n$ if
 \begin{align*}
\lim_{r\to 0}\frac{\operatorname{Cap}_1(A\cap B(x,r))}{r^{n-1}}=0.
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{\operatorname{Cap}_1(A\cap B(x,r))}{r^{n-1}}=0.
\end{align*} We also say that a set ![]() $U\subset {\mathbb R}^n$ is 1-finely open if
$U\subset {\mathbb R}^n$ is 1-finely open if ![]() ${\mathbb R}^n\setminus U$ is 1-thin at every
${\mathbb R}^n\setminus U$ is 1-thin at every ![]() $x\in U$. Then we define the 1-fine topology as the collection of 1-finely open sets on
$x\in U$. Then we define the 1-fine topology as the collection of 1-finely open sets on ![]() ${\mathbb R}^n$.
${\mathbb R}^n$.
We denote the 1-fine interior of a set ![]() $H\subset {\mathbb R}^n$, i.e. the largest 1-finely open set contained in H, by
$H\subset {\mathbb R}^n$, i.e. the largest 1-finely open set contained in H, by ![]() $\operatorname{fine-int} H$. We denote the 1-fine closure of H, i.e. the smallest 1-finely closed set containing H, by
$\operatorname{fine-int} H$. We denote the 1-fine closure of H, i.e. the smallest 1-finely closed set containing H, by ![]() $\overline{H}^1$. The 1-base
$\overline{H}^1$. The 1-base ![]() $b_1 H$ is defined as the set of points where H is not 1-thin.
$b_1 H$ is defined as the set of points where H is not 1-thin.
See [Reference Lahti17, Section 4] for discussion on definition 2.21, and for a proof of the fact that the 1-fine topology is indeed a topology. In fact, in [Reference Lahti17], the criterion
 \begin{align*}
\lim_{r\to 0}\frac{\operatorname{cap}_1(A\cap B(x,r),B(x,2r))}{r^{n-1}}=0
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{\operatorname{cap}_1(A\cap B(x,r),B(x,2r))}{r^{n-1}}=0
\end{align*}for 1-thinness was used, in the context of more general metric measure spaces. By (2.16) and lemma 2.17, this is equivalent with our current definition in the Euclidean setting.
According to [Reference Lahti16, corollary 3.5], the 1-fine closure of ![]() $A\subset {\mathbb R}^n$ can be characterized as
$A\subset {\mathbb R}^n$ can be characterized as
 \begin{align}
\overline{A}^1=A\cup b_1 A.
\end{align}
\begin{align}
\overline{A}^1=A\cup b_1 A.
\end{align}3. Proof of theorem 1.2
In this section, we prove theorem 1.2. We work in ![]() ${\mathbb R}^n$ with
${\mathbb R}^n$ with ![]() $n\ge 2$. First, we give the following simple example demonstrating that Kf is generally not a natural quantity to consider for mappings
$n\ge 2$. First, we give the following simple example demonstrating that Kf is generally not a natural quantity to consider for mappings  $f\in W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$, let alone mappings of lower regularity.
$f\in W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$, let alone mappings of lower regularity.
Example 3.1. Let ![]() $\{q_j\}_{j=1}^{\infty}$ be an enumeration of points in
$\{q_j\}_{j=1}^{\infty}$ be an enumeration of points in ![]() ${\mathbb R}^n$ with rational coordinates. Let
${\mathbb R}^n$ with rational coordinates. Let  $f\in W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$ be such that the first component function is
$f\in W_{\mathrm{loc}}^{1,n}({\mathbb R}^n;{\mathbb R}^n)$ be such that the first component function is
 \begin{align*}
f_1(x):=\sum_{j=1}^{\infty} 2^{-j}\log \max\{-\log|x-q_j|,1\},\quad x\in {\mathbb R}^n.
\end{align*}
\begin{align*}
f_1(x):=\sum_{j=1}^{\infty} 2^{-j}\log \max\{-\log|x-q_j|,1\},\quad x\in {\mathbb R}^n.
\end{align*} Now clearly ![]() $\operatorname{diam} f(B(x,r))=\infty$ for every
$\operatorname{diam} f(B(x,r))=\infty$ for every ![]() $x\in {\mathbb R}^n$ and r > 0. Thus
$x\in {\mathbb R}^n$ and r > 0. Thus
 \begin{align*}
K_f(x)=\limsup_{r\to 0}\left(\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}\right)^{1/(n-1)}
=\limsup_{r\to 0}\left(\frac{+\infty}{|f(B(x,r))|}\right)^{1/(n-1)}
\end{align*}
\begin{align*}
K_f(x)=\limsup_{r\to 0}\left(\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}\right)^{1/(n-1)}
=\limsup_{r\to 0}\left(\frac{+\infty}{|f(B(x,r))|}\right)^{1/(n-1)}
\end{align*} for every ![]() $x\in {\mathbb R}^n$, and so regardless of the value of
$x\in {\mathbb R}^n$, and so regardless of the value of ![]() $|f(B(x,r))|$, the quantity Kf is either
$|f(B(x,r))|$, the quantity Kf is either ![]() $+\infty$ or undefined.
$+\infty$ or undefined.
The Hardy–Littlewood maximal function of a function ![]() $u\in L^1_{\mathrm{loc}}({\mathbb R}^n)$ is defined by
$u\in L^1_{\mathrm{loc}}({\mathbb R}^n)$ is defined by
 \begin{align}
\mathcal M u(x):=\sup_{r \gt 0}\,-\!\!\!\!\!\!\int_{B(x,r)} |u|\,d\mathcal L^n,\quad x\in{\mathbb R}^n.
\end{align}
\begin{align}
\mathcal M u(x):=\sup_{r \gt 0}\,-\!\!\!\!\!\!\int_{B(x,r)} |u|\,d\mathcal L^n,\quad x\in{\mathbb R}^n.
\end{align} We also define a restricted version ![]() $\mathcal M_R u(x)$, with R > 0, by requiring
$\mathcal M_R u(x)$, with R > 0, by requiring ![]() $0 \lt r\le R$ in the supremum.
$0 \lt r\le R$ in the supremum.
It is well-known, see e.g. [Reference Kinnunen, Lehrbäck and Vähäkangas14, theorem 1.15], that
 \begin{align}
|\{x\in {\mathbb R}^n\colon \mathcal Mu(x) \gt t\}|\le \frac{C_0}{t}\Vert u\Vert_{L^1({\mathbb R}^n)},\quad t \gt 0,
\end{align}
\begin{align}
|\{x\in {\mathbb R}^n\colon \mathcal Mu(x) \gt t\}|\le \frac{C_0}{t}\Vert u\Vert_{L^1({\mathbb R}^n)},\quad t \gt 0,
\end{align}for a constant C 0 depending only on n.
The following weak-type estimate is standard, see e.g. [Reference Evans and Gariepy6, theorem 4.18]; in this reference, a slightly different definition for capacity is used, but a small modification of the proof gives the following result.
Lemma 3.4. Let ![]() $u\in \mathrm{BV}({\mathbb R}^n)$. Then for some constant C depending only on n, we have
$u\in \mathrm{BV}({\mathbb R}^n)$. Then for some constant C depending only on n, we have
 \begin{align*}
\operatorname{Cap}_1(\{\mathcal M u \gt t\}) \le C\frac{\Vert u\Vert_{\mathrm{BV}({\mathbb R}^n)}}{t}\quad\textrm{for all }t \gt 0.
\end{align*}
\begin{align*}
\operatorname{Cap}_1(\{\mathcal M u \gt t\}) \le C\frac{\Vert u\Vert_{\mathrm{BV}({\mathbb R}^n)}}{t}\quad\textrm{for all }t \gt 0.
\end{align*} We will need the following version of lemma 3.4; recall also the definition of ![]() $\mathcal M_R u$ from above that lemma.
$\mathcal M_R u$ from above that lemma.
Lemma 3.5. Let ![]() $u\in L^1({\mathbb R}^n)$. Then for some constant C depending only on n, we have
$u\in L^1({\mathbb R}^n)$. Then for some constant C depending only on n, we have
 \begin{align*}
\operatorname{Cap}_1(\{\mathcal M_1 u \gt t\}\cap B(x,1)) \le C\frac{\Vert u\Vert_{\mathrm{BV}(B(x,2))}}{t}\quad\textrm{for all }t \gt 0.
\end{align*}
\begin{align*}
\operatorname{Cap}_1(\{\mathcal M_1 u \gt t\}\cap B(x,1)) \le C\frac{\Vert u\Vert_{\mathrm{BV}(B(x,2))}}{t}\quad\textrm{for all }t \gt 0.
\end{align*}Proof. We can assume that ![]() $\Vert u\Vert_{\mathrm{BV}(B(x,2))}$ is finite. Denote by Eu an extension of u from
$\Vert u\Vert_{\mathrm{BV}(B(x,2))}$ is finite. Denote by Eu an extension of u from ![]() $B(x,2)$ to
$B(x,2)$ to ![]() ${\mathbb R}^n$ with
${\mathbb R}^n$ with ![]() $\Vert Eu\Vert_{\mathrm{BV}({\mathbb R}^n)}\le C' \Vert u\Vert_{\mathrm{BV}(B(x,2))}$, for some Cʹ depending only on n; see e.g. [Reference Ambrosio, Fusco and Pallara1, proposition 3.21]. We estimate
$\Vert Eu\Vert_{\mathrm{BV}({\mathbb R}^n)}\le C' \Vert u\Vert_{\mathrm{BV}(B(x,2))}$, for some Cʹ depending only on n; see e.g. [Reference Ambrosio, Fusco and Pallara1, proposition 3.21]. We estimate
 \begin{align*}
\operatorname{Cap}_1(\{\mathcal M_1 u \gt t\}\cap B(x,1))
&= \operatorname{Cap}_1(\{\mathcal M_1 Eu \gt t\}\cap B(x,1))\\
&\le \operatorname{Cap}_1(\{\mathcal M_1 Eu \gt t\})\\
&\le C\frac{\Vert Eu \Vert_{\mathrm{BV}({\mathbb R}^n)}}{t}\quad\textrm{by lemma 3.4}\\
&\le CC'\frac{\Vert u \Vert_{\mathrm{BV}(B(x,2))}}{t}.
\end{align*}
\begin{align*}
\operatorname{Cap}_1(\{\mathcal M_1 u \gt t\}\cap B(x,1))
&= \operatorname{Cap}_1(\{\mathcal M_1 Eu \gt t\}\cap B(x,1))\\
&\le \operatorname{Cap}_1(\{\mathcal M_1 Eu \gt t\})\\
&\le C\frac{\Vert Eu \Vert_{\mathrm{BV}({\mathbb R}^n)}}{t}\quad\textrm{by lemma 3.4}\\
&\le CC'\frac{\Vert u \Vert_{\mathrm{BV}(B(x,2))}}{t}.
\end{align*}It is known that Sobolev and BV functions are approximately differentiable a.e., in the sense of (3.7) below. In the following theorem, we show a stronger property, namely that these functions are also 1-finely differentiable a.e.
Recall the definition of the precise representative from (2.10). Recall also that we denote by ![]() $\nabla f$ the density of the absolutely continuous part of Df.
$\nabla f$ the density of the absolutely continuous part of Df.
Theorem 3.6. Let ![]() $\Omega\subset {\mathbb R}^n$ be open and let
$\Omega\subset {\mathbb R}^n$ be open and let ![]() $f\in \mathrm{BV}_{\mathrm{loc}}(\Omega;{\mathbb R}^l)$, with
$f\in \mathrm{BV}_{\mathrm{loc}}(\Omega;{\mathbb R}^l)$, with ![]() $l\in{\mathbb N}$. Then for a.e.
$l\in{\mathbb N}$. Then for a.e. ![]() $x\in \Omega$ there exists a 1-finely open set
$x\in \Omega$ there exists a 1-finely open set ![]() $U\ni x$ such that
$U\ni x$ such that
 \begin{align*}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f^*(y)-f^*(x)-\nabla f(x)(y-x)|}{|y-x|}=0.
\end{align*}
\begin{align*}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f^*(y)-f^*(x)-\nabla f(x)(y-x)|}{|y-x|}=0.
\end{align*}Proof. Since the issue is local, we can assume that ![]() $\Omega={\mathbb R}^n$. First assume also that l = 1. At a.e.
$\Omega={\mathbb R}^n$. First assume also that l = 1. At a.e. ![]() $x\in{\mathbb R}^n$, we have
$x\in{\mathbb R}^n$, we have
 \begin{align}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} \frac{|f(y)-f^*(x)-\langle \nabla f(x), y-x\rangle|}{r}\,d\mathcal L^n(y)=0,
\end{align}
\begin{align}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} \frac{|f(y)-f^*(x)-\langle \nabla f(x), y-x\rangle|}{r}\,d\mathcal L^n(y)=0,
\end{align}see [Reference Ambrosio, Fusco and Pallara1, theorem 3.83], as well as
 \begin{align*}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} |\nabla f(y)-\nabla f(x)|\,d\mathcal L^n(y)=0
\quad\textrm{and}\quad
\lim_{r\to 0}\frac{|D^s f|(B(x,r))}{r^n}=0.
\end{align*}
\begin{align*}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} |\nabla f(y)-\nabla f(x)|\,d\mathcal L^n(y)=0
\quad\textrm{and}\quad
\lim_{r\to 0}\frac{|D^s f|(B(x,r))}{r^n}=0.
\end{align*} Consider such x. Define ![]() $L(z):=\langle \nabla u(x),z\rangle$. Thus for the scalings
$L(z):=\langle \nabla u(x),z\rangle$. Thus for the scalings
 \begin{align}
f_{x,r}(z):=\frac{f(x+rz)-f^*(x)}{r},\quad z\in B(0,2),
\end{align}
\begin{align}
f_{x,r}(z):=\frac{f(x+rz)-f^*(x)}{r},\quad z\in B(0,2),
\end{align}we have
 \begin{align*}
f_{x,r}(\cdot)\to L(\cdot)\ \ \textrm{in }L^1(B(0,2))\,\textrm{as }r\to 0
\quad\textrm{and}\quad
\nabla f_{x,r}(z) = \nabla f(x+rz),\ z\in B(0,2).
\end{align*}
\begin{align*}
f_{x,r}(\cdot)\to L(\cdot)\ \ \textrm{in }L^1(B(0,2))\,\textrm{as }r\to 0
\quad\textrm{and}\quad
\nabla f_{x,r}(z) = \nabla f(x+rz),\ z\in B(0,2).
\end{align*}Then
 \begin{align*}
|D (f_{x,r}-L)|(B(0,2))
&=\int_{B(0,2)}|\nabla f_{x,r}(z)-\nabla f(x)|\,d\mathcal L^n(z)+|D^s f_{x,r}|(B(0,2))\\
&=\frac{1}{r^n}\int_{B(x,2r)}|\nabla f(y)-\nabla f(x)|\,d\mathcal L^n(y)+\frac{|D^s f|(B(x,2r))}{r^n}\\
&\to 0\quad\textrm{as }r\to 0.
\end{align*}
\begin{align*}
|D (f_{x,r}-L)|(B(0,2))
&=\int_{B(0,2)}|\nabla f_{x,r}(z)-\nabla f(x)|\,d\mathcal L^n(z)+|D^s f_{x,r}|(B(0,2))\\
&=\frac{1}{r^n}\int_{B(x,2r)}|\nabla f(y)-\nabla f(x)|\,d\mathcal L^n(y)+\frac{|D^s f|(B(x,2r))}{r^n}\\
&\to 0\quad\textrm{as }r\to 0.
\end{align*}In conclusion, we have the norm convergence
Note that ![]() $(f^*)_{x,r}=(f_{x,r})^*$ in
$(f^*)_{x,r}=(f_{x,r})^*$ in ![]() $B(0,2)$, so we simply use the notation
$B(0,2)$, so we simply use the notation ![]() $f^*_{x,r}$. Note also that
$f^*_{x,r}$. Note also that
and so for every ![]() $j\in{\mathbb N}$ and t > 0 we get
$j\in{\mathbb N}$ and t > 0 we get
 \begin{align*}
&\operatorname{Cap}_1(\{z\in B(0,1)\colon |f^*_{x,2^{-j}}(z)-L(z)| \gt t\})\\
&\qquad \le \operatorname{Cap}_1(\{z\in B(0,1)\colon \mathcal M_1|f_{x,2^{-j}}-L|(z) \gt t\})\\
&\qquad \le C\frac{\Vert f_{x,2^{-j}}-L\Vert_{\mathrm{BV}(B(0,2))}}{t}\quad \textrm{by lemma 3.5}\\
&\qquad \to 0\quad\textrm{as }j\to\infty\quad \textrm{by (3.9)}.
\end{align*}
\begin{align*}
&\operatorname{Cap}_1(\{z\in B(0,1)\colon |f^*_{x,2^{-j}}(z)-L(z)| \gt t\})\\
&\qquad \le \operatorname{Cap}_1(\{z\in B(0,1)\colon \mathcal M_1|f_{x,2^{-j}}-L|(z) \gt t\})\\
&\qquad \le C\frac{\Vert f_{x,2^{-j}}-L\Vert_{\mathrm{BV}(B(0,2))}}{t}\quad \textrm{by lemma 3.5}\\
&\qquad \to 0\quad\textrm{as }j\to\infty\quad \textrm{by (3.9)}.
\end{align*} Thus we can choose numbers ![]() $t_j\searrow 0$ such that for the sets
$t_j\searrow 0$ such that for the sets
 \begin{align*}
D_j:=\{z\in B(0,1)\colon |f^*_{x,2^{-j}}(z)-L(z)| \gt t_j\},
\end{align*}
\begin{align*}
D_j:=\{z\in B(0,1)\colon |f^*_{x,2^{-j}}(z)-L(z)| \gt t_j\},
\end{align*} we get ![]() $\operatorname{Cap}_1(D_j)\to 0$ as
$\operatorname{Cap}_1(D_j)\to 0$ as ![]() $j\to\infty$. Define
$j\to\infty$. Define ![]() $A_j:=D_j\setminus B(0,1/2)$ and
$A_j:=D_j\setminus B(0,1/2)$ and  $A:=\bigcup_{j=1}^{\infty}2^{-j}A_j+x$. Now for all
$A:=\bigcup_{j=1}^{\infty}2^{-j}A_j+x$. Now for all ![]() $k\in{\mathbb N}$, we have
$k\in{\mathbb N}$, we have
 \begin{align*}
\operatorname{Cap}_1(A\cap B(x,2^{-k}))
&\le \sum_{j=k}^{\infty}\operatorname{Cap}_1(2^{-j}A_j+x)\\
&= \sum_{j=k}^{\infty}2^{-j(n-1)}\operatorname{Cap}_1(A_j)\\
&\le \sum_{j=k}^{\infty}2^{-j(n-1)}\operatorname{Cap}_1(D_j)\\
&\le 2^{-k(n-1)+1}\max_{j\ge k}\operatorname{Cap}_1(D_j).
\end{align*}
\begin{align*}
\operatorname{Cap}_1(A\cap B(x,2^{-k}))
&\le \sum_{j=k}^{\infty}\operatorname{Cap}_1(2^{-j}A_j+x)\\
&= \sum_{j=k}^{\infty}2^{-j(n-1)}\operatorname{Cap}_1(A_j)\\
&\le \sum_{j=k}^{\infty}2^{-j(n-1)}\operatorname{Cap}_1(D_j)\\
&\le 2^{-k(n-1)+1}\max_{j\ge k}\operatorname{Cap}_1(D_j).
\end{align*} Since ![]() $\operatorname{Cap}_1(D_j)\to 0$, we obtain
$\operatorname{Cap}_1(D_j)\to 0$, we obtain
 \begin{align*}
\frac{\operatorname{Cap}_1(A\cap B(0,2^{-k}))}{2^{-k(n-1)}}\to 0\quad
\textrm{as }k\to\infty,
\end{align*}
\begin{align*}
\frac{\operatorname{Cap}_1(A\cap B(0,2^{-k}))}{2^{-k(n-1)}}\to 0\quad
\textrm{as }k\to\infty,
\end{align*} and so clearly A is 1-thin at x. By (2.22), the 1-finely open set  $U:={\mathbb R}^n\setminus \overline{A}^1$ contains x. For any
$U:={\mathbb R}^n\setminus \overline{A}^1$ contains x. For any ![]() $j\in{\mathbb N}$ and
$j\in{\mathbb N}$ and ![]() $y\in U\cap B(x,2^{-j})\setminus B(x,2^{-j-1})$, we have
$y\in U\cap B(x,2^{-j})\setminus B(x,2^{-j-1})$, we have
 \begin{align*}
\frac{|f^*(y)-f^*(x)-L(y-x)|}{|y-x|}
&\le 2\frac{|f^*(y)-f^*(x)-L(y-x)|}{2^{-j}}\\
&= 2|f^*_{x,2^{-j}}((y-x)/2^{-j})-L((y-x)/2^{-j})|\\
&\le 2t_j\to 0\quad\textrm{as }j\to\infty,
\end{align*}
\begin{align*}
\frac{|f^*(y)-f^*(x)-L(y-x)|}{|y-x|}
&\le 2\frac{|f^*(y)-f^*(x)-L(y-x)|}{2^{-j}}\\
&= 2|f^*_{x,2^{-j}}((y-x)/2^{-j})-L((y-x)/2^{-j})|\\
&\le 2t_j\to 0\quad\textrm{as }j\to\infty,
\end{align*}and so
 \begin{align*}
\lim_{U\ni y\to x}\frac{|f^*(y)-f^*(x)-\langle\nabla f(x), y-x\rangle|}{|y-x|}=0.
\end{align*}
\begin{align*}
\lim_{U\ni y\to x}\frac{|f^*(y)-f^*(x)-\langle\nabla f(x), y-x\rangle|}{|y-x|}=0.
\end{align*} Finally, the generalization to the case ![]() $l\in{\mathbb N}$ is immediate, since the intersection of a finite number of 1-finely open sets is still 1-finely open.
$l\in{\mathbb N}$ is immediate, since the intersection of a finite number of 1-finely open sets is still 1-finely open.
Given  $f\in W^{1,1}_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, note that the weak gradient
$f\in W^{1,1}_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$, note that the weak gradient ![]() $\nabla f$ is a function in
$\nabla f$ is a function in ![]() $L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^{n\times n})$ and thus may be understood to be an equivalence class rather than a pointwise defined function. Below, we sometimes consider
$L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^{n\times n})$ and thus may be understood to be an equivalence class rather than a pointwise defined function. Below, we sometimes consider ![]() $\nabla f$ at a given point; for this, we can understand
$\nabla f$ at a given point; for this, we can understand ![]() $\nabla f$ to be well defined everywhere by using the above theorem and by defining
$\nabla f$ to be well defined everywhere by using the above theorem and by defining ![]() $\nabla f$ to be zero in the exceptional set.
$\nabla f$ to be zero in the exceptional set.
We restate the following definition already given in §1.
Definition 3.10. Let ![]() $f\colon {\mathbb R}^n\to [-\infty,\infty]^{n}$ and
$f\colon {\mathbb R}^n\to [-\infty,\infty]^{n}$ and ![]() $U\subset {\mathbb R}^n$. Then we let
$U\subset {\mathbb R}^n$. Then we let
 \begin{align*}
K_{f,U}(x,r):=\left(\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|f(B(x,r))|}\right)^{1/(n-1)}\quad\textrm{and}\quad
K_{f}^{\mathrm{fine}}(x):=\inf\limsup_{r\to 0}K_{f,U}(x,r),
\end{align*}
\begin{align*}
K_{f,U}(x,r):=\left(\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|f(B(x,r))|}\right)^{1/(n-1)}\quad\textrm{and}\quad
K_{f}^{\mathrm{fine}}(x):=\inf\limsup_{r\to 0}K_{f,U}(x,r),
\end{align*} where the infimum is taken over 1-finely open sets ![]() $U\ni x$. If
$U\ni x$. If ![]() $|f(B(x,r))|=0$, then we interpret
$|f(B(x,r))|=0$, then we interpret ![]() $K_{f,U}(x,r)=\infty$.
$K_{f,U}(x,r)=\infty$.
Proof of theorem 1.2
Let  $f\in W^{1,1}_{\mathrm{loc}}({\mathbb R}^n;{\mathbb R}^n)$; since the claim is local, we can assume that in fact
$f\in W^{1,1}_{\mathrm{loc}}({\mathbb R}^n;{\mathbb R}^n)$; since the claim is local, we can assume that in fact ![]() $f\in W^{1,1}({\mathbb R}^n;{\mathbb R}^n)$. Using, e.g., [Reference Evans and Gariepy6, theorem 6.15], we find a Lipschitz mapping
$f\in W^{1,1}({\mathbb R}^n;{\mathbb R}^n)$. Using, e.g., [Reference Evans and Gariepy6, theorem 6.15], we find a Lipschitz mapping  $\widehat{f}\in \operatorname{Lip}({\mathbb R}^n;{\mathbb R}^n)$ such that the complement of the set
$\widehat{f}\in \operatorname{Lip}({\mathbb R}^n;{\mathbb R}^n)$ such that the complement of the set
 \begin{align*}
H:=\{z\in {\mathbb R}^n\colon (\widehat{f})^*(z)= f^*(z)
\ \textrm{and}\ \nabla \widehat{f}(z)= \nabla f(z)\}
\end{align*}
\begin{align*}
H:=\{z\in {\mathbb R}^n\colon (\widehat{f})^*(z)= f^*(z)
\ \textrm{and}\ \nabla \widehat{f}(z)= \nabla f(z)\}
\end{align*} has arbitrarily small Lebesgue measure. By, e.g., [Reference Ambrosio, Fusco and Pallara1, lemma 2.74], ![]() $\mathcal L^n$-almost all of the set
$\mathcal L^n$-almost all of the set  $\{z\in{\mathbb R}^n\colon \det \nabla \widehat{f}(z)\neq 0\}$ can be covered by compact sets
$\{z\in{\mathbb R}^n\colon \det \nabla \widehat{f}(z)\neq 0\}$ can be covered by compact sets ![]() $\{K_j\}_{j=1}^{\infty}$ such that
$\{K_j\}_{j=1}^{\infty}$ such that ![]() $\widehat{f}$ is injective in each Kj. Consider a point
$\widehat{f}$ is injective in each Kj. Consider a point ![]() $x\in{\mathbb R}^n$ for which
$x\in{\mathbb R}^n$ for which ![]() $\det \nabla f(x)\neq 0$. Since the theorem is formulated as an ‘a.e.’ result, we can assume that
$\det \nabla f(x)\neq 0$. Since the theorem is formulated as an ‘a.e.’ result, we can assume that
 \begin{align*}
\lim_{r\to 0}\frac{|B(x,r)\cap H|}{|B(x,r)|}=1
\quad\textrm{and}\quad
\lim_{r\to 0}\frac{|B(x,r)\cap K_j|}{|B(x,r)|}=1
\quad\textrm{for some }j,
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{|B(x,r)\cap H|}{|B(x,r)|}=1
\quad\textrm{and}\quad
\lim_{r\to 0}\frac{|B(x,r)\cap K_j|}{|B(x,r)|}=1
\quad\textrm{for some }j,
\end{align*} that f is 1-finely differentiable as in theorem 3.6 so that we find a 1-finely open set ![]() $U\ni x$ such that
$U\ni x$ such that
 \begin{align}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f^*(y)-f^*(x)-\nabla f(x)(y-x)|}{|y-x|}=0,
\end{align}
\begin{align}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f^*(y)-f^*(x)-\nabla f(x)(y-x)|}{|y-x|}=0,
\end{align} and that x is a Lebesgue point of ![]() $\nabla f$:
$\nabla f$:
 \begin{align}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} | \nabla f(y)-\nabla f(x)| \,d\mathcal L^n(y)=0.
\end{align}
\begin{align}
\lim_{r\to 0}\,-\!\!\!\!\!\!\int_{B(x,r)} | \nabla f(y)-\nabla f(x)| \,d\mathcal L^n(y)=0.
\end{align}For the scalings
 \begin{align*}
f_{r}(z):=\frac{f^*(x+rz)-f^*(x)}{r},\quad z\in B(0,1),
\end{align*}
\begin{align*}
f_{r}(z):=\frac{f^*(x+rz)-f^*(x)}{r},\quad z\in B(0,1),
\end{align*} we have ![]() $\nabla f_{r}(z) = \nabla f(x+rz)$, with
$\nabla f_{r}(z) = \nabla f(x+rz)$, with ![]() $z\in B(0,1)$, and thus by (3.12),
$z\in B(0,1)$, and thus by (3.12),
 \begin{align}
\lim_{r\to 0}\int_{B(0,1)}|\nabla f_{r} -\nabla f(x)|\,d\mathcal L^n =0.
\end{align}
\begin{align}
\lim_{r\to 0}\int_{B(0,1)}|\nabla f_{r} -\nabla f(x)|\,d\mathcal L^n =0.
\end{align}Fix ɛ > 0. Let
By (3.13), we also have ![]() $|B(0,1)\setminus D^r| \lt \omega_n\varepsilon$ for sufficiently small r > 0. Let
$|B(0,1)\setminus D^r| \lt \omega_n\varepsilon$ for sufficiently small r > 0. Let
For sufficiently small r > 0, we have in total
In the set ![]() $D^r\cap H_r\cap (K_j)_r$, we have
$D^r\cap H_r\cap (K_j)_r$, we have
 \begin{align}
\begin{split}
|\det \nabla \widehat{f}_r|
=|\det \nabla f_r|
\ge (1-\varepsilon)|\det \nabla f(x)|.
\end{split}
\end{align}
\begin{align}
\begin{split}
|\det \nabla \widehat{f}_r|
=|\det \nabla f_r|
\ge (1-\varepsilon)|\det \nabla f(x)|.
\end{split}
\end{align}Now by the area formula, see e.g. [Reference Ambrosio, Fusco and Pallara1, theorem 2.71], we get
 \begin{align*}
|f_r(B(0,1))|
&\ge |f_r(D^r\cap H_r\cap (K_j)_r)|\\
&=|\widehat{f}_r(D^r\cap H_r\cap (K_j)_r)|\\
&=\int_{D^r\cap H_r\cap (K_j)_r}|\det \nabla \widehat{f}_r|\,d\mathcal L^n\\
&\ge (1-\varepsilon)\int_{D^r\cap H_r\cap (K_j)_r}|\det \nabla f(x)|\,d\mathcal L^n
\quad \textrm{by (3.15)}\\
&\ge (1-\varepsilon)^2 \omega_n |\det \nabla f(x)|\quad \textrm{by (3.14)}.
\end{align*}
\begin{align*}
|f_r(B(0,1))|
&\ge |f_r(D^r\cap H_r\cap (K_j)_r)|\\
&=|\widehat{f}_r(D^r\cap H_r\cap (K_j)_r)|\\
&=\int_{D^r\cap H_r\cap (K_j)_r}|\det \nabla \widehat{f}_r|\,d\mathcal L^n\\
&\ge (1-\varepsilon)\int_{D^r\cap H_r\cap (K_j)_r}|\det \nabla f(x)|\,d\mathcal L^n
\quad \textrm{by (3.15)}\\
&\ge (1-\varepsilon)^2 \omega_n |\det \nabla f(x)|\quad \textrm{by (3.14)}.
\end{align*}Thus
Thus using also the fine differentiability (3.11), we get
 \begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f^*(B(x,r)\cap U)^n}{|f^*(B(x,r))|}
&\le \limsup_{r\to 0}\frac{2^n\Vert \nabla f(x)\Vert^n
r^n}{(1-\varepsilon)^2 \omega_n r^n |\det \nabla f(x)|}\\
&=\frac{2^n\Vert \nabla f(x)\Vert^n}{(1-\varepsilon)^2 \omega_n |\det \nabla f(x)|}.
\end{align*}
\begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f^*(B(x,r)\cap U)^n}{|f^*(B(x,r))|}
&\le \limsup_{r\to 0}\frac{2^n\Vert \nabla f(x)\Vert^n
r^n}{(1-\varepsilon)^2 \omega_n r^n |\det \nabla f(x)|}\\
&=\frac{2^n\Vert \nabla f(x)\Vert^n}{(1-\varepsilon)^2 \omega_n |\det \nabla f(x)|}.
\end{align*}It follows that
 \begin{align*}
(1-\varepsilon)^2 K_{f^*}^{\mathrm{fine}}(x) ^{n-1}|\det \nabla f(x)|
\le \frac{2^n}{\omega_n}\Vert \nabla f(x)\Vert^n.
\end{align*}
\begin{align*}
(1-\varepsilon)^2 K_{f^*}^{\mathrm{fine}}(x) ^{n-1}|\det \nabla f(x)|
\le \frac{2^n}{\omega_n}\Vert \nabla f(x)\Vert^n.
\end{align*}Letting ɛ → 0, we get the result.
4. Proof of theorem 1.3
In this section, we prove our main theorem 1.3. At first, we work in ![]() ${\mathbb R}^n$ with
${\mathbb R}^n$ with ![]() $n\ge 2$, but in our main results we need n = 2. We start with the following simple lemma.
$n\ge 2$, but in our main results we need n = 2. We start with the following simple lemma.
Lemma 4.1. Assume ![]() $\Omega\subset {\mathbb R}^n$ is open,
$\Omega\subset {\mathbb R}^n$ is open,  $f\in W^{1,1}_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$ is continuous,
$f\in W^{1,1}_{\mathrm{loc}}(\Omega;{\mathbb R}^n)$ is continuous, ![]() $x\in\Omega$, and suppose
$x\in\Omega$, and suppose ![]() $U\ni x$ is a 1-finely open set such that
$U\ni x$ is a 1-finely open set such that
 \begin{align}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f(y)-f(x)-\nabla f(x) (y-x)|}{|y-x|}=0.
\end{align}
\begin{align}
\lim_{U\setminus \{x\}\ni y\to x}\frac{|f(y)-f(x)-\nabla f(x) (y-x)|}{|y-x|}=0.
\end{align}Then
 \begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|B(x,r)|}
= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n.
\end{align*}
\begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|B(x,r)|}
= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n.
\end{align*}Proof. By lemma 2.17, we have
 \begin{align*}
\lim_{r\to 0}\frac{|B(x,r)\setminus U|}{|B(x,r)|}=0,
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{|B(x,r)\setminus U|}{|B(x,r)|}=0,
\end{align*} and so for the linear mapping ![]() $L(y):=\nabla f(x)(y-x)$, we clearly have
$L(y):=\nabla f(x)(y-x)$, we clearly have
 \begin{align*}
\lim_{r\to 0}\frac{\operatorname{diam} L(B(x,r)\cap U)}{r}=2\Vert \nabla f(x)\Vert.
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{\operatorname{diam} L(B(x,r)\cap U)}{r}=2\Vert \nabla f(x)\Vert.
\end{align*}Then by the fine differentiability (4.2), we also have
 \begin{align*}
\lim_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)}{r}= 2\Vert\nabla f(x)\Vert,
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)}{r}= 2\Vert\nabla f(x)\Vert,
\end{align*}and so the claim follows.
Now we show that the following version of theorem 1.2 holds when f is additionally assumed to be a homeomorphism; recall (2.1).
Proposition 4.3. Let ![]() $\Omega,\Omega'\subset {\mathbb R}^n$ be open and let
$\Omega,\Omega'\subset {\mathbb R}^n$ be open and let  $f\in W_{\mathrm{loc}}^{1,1}(\Omega;\Omega')$ be a homeomorphism. Then we have
$f\in W_{\mathrm{loc}}^{1,1}(\Omega;\Omega')$ be a homeomorphism. Then we have
 \begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in \Omega\,\textrm{ for which }K_f^{\mathrm{fine}}(x) \lt \infty,
\end{align*}
\begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\quad \textrm{for a.e. }x\in \Omega\,\textrm{ for which }K_f^{\mathrm{fine}}(x) \lt \infty,
\end{align*} and  $K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e.
$K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e. ![]() $x\in \Omega$ where f is differentiable and
$x\in \Omega$ where f is differentiable and ![]() $0 \lt J_f(x) \lt \infty$.
$0 \lt J_f(x) \lt \infty$.
Proof. Consider ![]() $x\in\Omega$ for which
$x\in\Omega$ for which  $K_f^{\mathrm{fine}}(x) \lt \infty$. Thus, we find a 1-finely open set
$K_f^{\mathrm{fine}}(x) \lt \infty$. Thus, we find a 1-finely open set ![]() $V\ni x$ such that
$V\ni x$ such that
 \begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V)^n}{|f(B(x,r))|} \lt \infty.
\end{align*}
\begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V)^n}{|f(B(x,r))|} \lt \infty.
\end{align*} Excluding a ![]() $\mathcal L^n$-negligible set, we can also assume that
$\mathcal L^n$-negligible set, we can also assume that ![]() $J_f(x) \lt \infty$ exists as a limit (recall the discussion after (2.1)), and that we find a 1-finely open set
$J_f(x) \lt \infty$ exists as a limit (recall the discussion after (2.1)), and that we find a 1-finely open set ![]() $U\ni x$ with
$U\ni x$ with
 \begin{align*}
\lim_{U\setminus\{x\}\ni y\to x}\frac{|f(y)-f(x)-\nabla f(x)(y-x)|}{|y-x|}=0,
\end{align*}
\begin{align*}
\lim_{U\setminus\{x\}\ni y\to x}\frac{|f(y)-f(x)-\nabla f(x)(y-x)|}{|y-x|}=0,
\end{align*}recall theorem 3.6. To prove one inequality, we estimate
 \begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)
&\le \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}
\frac{|f(B(x,r))|}{|B(x,r)|}\\
&\le \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\end{align*}
\begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)
&\le \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}
\frac{|f(B(x,r))|}{|B(x,r)|}\\
&\le \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U)^n}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n
\end{align*}by lemma 4.1.
Then we prove the opposite inequality. Let ɛ > 0. We can choose the 1-finely open set ![]() $V\ni x$ such that
$V\ni x$ such that
 \begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}
& \gt \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V)^n}{|f(B(x,r))|}-\varepsilon\\
&\ge \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}-\varepsilon.
\end{align*}
\begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}
& \gt \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V)^n}{|f(B(x,r))|}-\varepsilon\\
&\ge \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}-\varepsilon.
\end{align*}Then
 \begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)
&\ge \left(\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}-\varepsilon\right)
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|B(x,r)|}-\lim_{r\to 0}\varepsilon\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n-\varepsilon J_f(x)
\end{align*}
\begin{align*}
K_f^{\mathrm{fine}}(x)^{n-1}J_f(x)
&\ge \left(\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|f(B(x,r))|}-\varepsilon\right)
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap V\cap U)^n}{|B(x,r)|}-\lim_{r\to 0}\varepsilon\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n-\varepsilon J_f(x)
\end{align*}by lemma 4.1. Letting ɛ → 0, we get the other inequality.
If f is differentiable at ![]() $x\in\Omega$ and
$x\in\Omega$ and ![]() $0 \lt J_f(x) \lt \infty$, we can again assume that
$0 \lt J_f(x) \lt \infty$, we can again assume that ![]() $J_f(x)$ exists as a limit, and then we also have
$J_f(x)$ exists as a limit, and then we also have
 \begin{align*}
K_f(x)^{n-1}J_f(x)
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r))^n}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n,
\end{align*}
\begin{align*}
K_f(x)^{n-1}J_f(x)
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r))^n}{|f(B(x,r))|}
\lim_{r\to 0}\frac{|f(B(x,r))|}{|B(x,r)|}\\
&= \limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r))^n}{|B(x,r)|}\\
&= \frac{2^n}{\omega_n} \Vert \nabla f(x)\Vert^n,
\end{align*}and so
 \begin{align*}
K_f(x)^{n-1}
=\frac{2^n}{\omega_n} \frac{\Vert \nabla f(x)\Vert^n}{J_f(x)}
=K_f^{\mathrm{fine}}(x)^{n-1},
\end{align*}
\begin{align*}
K_f(x)^{n-1}
=\frac{2^n}{\omega_n} \frac{\Vert \nabla f(x)\Vert^n}{J_f(x)}
=K_f^{\mathrm{fine}}(x)^{n-1},
\end{align*} where we also used the first part of the proposition, which is applicable since  $K_f^{\mathrm{fine}}(x)\le K_f(x) \lt \infty$.
$K_f^{\mathrm{fine}}(x)\le K_f(x) \lt \infty$.
We note that Eq. (1.1) in §1 can be proved similarly to proposition 4.3.
We will use Whitney-type coverings consisting of disks. As with balls so far, a disk is always understood to be open unless otherwise specified.
Lemma 4.4. Let ![]() $A\subset D\subset W$, where
$A\subset D\subset W$, where ![]() $W\subset {\mathbb R}^2$ is an open set and A is dense in D. Given a scale
$W\subset {\mathbb R}^2$ is an open set and A is dense in D. Given a scale ![]() $0 \lt R \lt \infty$, there exists a finite or countable Whitney-type covering
$0 \lt R \lt \infty$, there exists a finite or countable Whitney-type covering ![]() $\{B_k=B(x_k,r_k)\}_k$ of A in W, with
$\{B_k=B(x_k,r_k)\}_k$ of A in W, with ![]() $x_k\in A$,
$x_k\in A$, ![]() $r_k\le R$, and the following properties:
$r_k\le R$, and the following properties:
(1)
 $B_k\subset W$ and
$B_k\subset W$ and  $D\subset \bigcup_{k}\tfrac 12 B_k$,
$D\subset \bigcup_{k}\tfrac 12 B_k$,(2) If
 $B_k\cap B_l\neq \emptyset$, then
$B_k\cap B_l\neq \emptyset$, then  $r_{k}\le 2r_{l}$;
$r_{k}\le 2r_{l}$;(3) The disks Bk can be divided into 6400 collections of pairwise disjoint disks.
Proof. For every ![]() $x\in A$, let
$x\in A$, let  $r_x:=\min\{R,\tfrac{1}{4} \operatorname{dist}(x,{\mathbb R}^n\setminus W)\}$. Consider the covering
$r_x:=\min\{R,\tfrac{1}{4} \operatorname{dist}(x,{\mathbb R}^n\setminus W)\}$. Consider the covering  $\{B(x,\frac{1}{10}r_x)\}_{x\in A}$. Clearly this is also a covering of D. By the 5-covering theorem (see e.g. [Reference Evans and Gariepy6, theorem 1.24]), we can pick an at most countable collection of pairwise disjoint disks
$\{B(x,\frac{1}{10}r_x)\}_{x\in A}$. Clearly this is also a covering of D. By the 5-covering theorem (see e.g. [Reference Evans and Gariepy6, theorem 1.24]), we can pick an at most countable collection of pairwise disjoint disks  $B(x_k,\tfrac{1}{10}r_k)$ such that the disks
$B(x_k,\tfrac{1}{10}r_k)$ such that the disks  $B(x_k,\tfrac{1}{2} r_k)$ cover D. Denote
$B(x_k,\tfrac{1}{2} r_k)$ cover D. Denote ![]() $B_k=B(x_k,r_k)$. We have established property (1).
$B_k=B(x_k,r_k)$. We have established property (1).
Suppose ![]() $B_k\cap B_l\neq \emptyset$. If
$B_k\cap B_l\neq \emptyset$. If  $r_l=\tfrac{1}{4} \operatorname{dist}(x_l,{\mathbb R}^n\setminus W)$, then
$r_l=\tfrac{1}{4} \operatorname{dist}(x_l,{\mathbb R}^n\setminus W)$, then
and so we get ![]() $2r_l\ge r_k$. If
$2r_l\ge r_k$. If ![]() $r_l=R$, then
$r_l=R$, then ![]() $r_k\le R=r_l$. Thus we get property (2).
$r_k\le R=r_l$. Thus we get property (2).
For a given k, denote by I the set of those indices ![]() $l\in I$ such that
$l\in I$ such that ![]() $B_l\cap B_k\neq \emptyset$. For all
$B_l\cap B_k\neq \emptyset$. For all ![]() $l\in I$, by (2), we have
$l\in I$, by (2), we have ![]() $r_k\le 2r_l$ and
$r_k\le 2r_l$ and  $\tfrac{1}{10}B_l\subset 4B_k$, and so
$\tfrac{1}{10}B_l\subset 4B_k$, and so
 \begin{align*}
\sum_{l\in I}400^{-1}\pi r_k^2
\le \sum_{l\in I}100^{-1}\pi r_l^2
= \sum_{l\in I} \mathcal L^2(\tfrac{1}{10} B_l)
\le \mathcal L^2(4B_k)
= 16 \pi r_k^2,
\end{align*}
\begin{align*}
\sum_{l\in I}400^{-1}\pi r_k^2
\le \sum_{l\in I}100^{-1}\pi r_l^2
= \sum_{l\in I} \mathcal L^2(\tfrac{1}{10} B_l)
\le \mathcal L^2(4B_k)
= 16 \pi r_k^2,
\end{align*}and so the cardinality of I is at most 6400, and we obtain (3).
Lemma 4.5. Let ![]() $A\subset {\mathbb R}^2$. Then
$A\subset {\mathbb R}^2$. Then ![]() $\mathcal H^1_{\infty}(A)\le 10\operatorname{Cap}_1(A)$.
$\mathcal H^1_{\infty}(A)\le 10\operatorname{Cap}_1(A)$.
Proof. We can assume that ![]() $\operatorname{Cap}_1(A) \lt \infty$. Let ɛ > 0. We find a function
$\operatorname{Cap}_1(A) \lt \infty$. Let ɛ > 0. We find a function ![]() $u\in W^{1,1}({\mathbb R}^2)$ such that
$u\in W^{1,1}({\mathbb R}^2)$ such that ![]() $u\ge 1$ in a neighbourhood of A and
$u\ge 1$ in a neighbourhood of A and
 \begin{align*}
\int_{{\mathbb R}^2} |\nabla u|\,d\mathcal L^2\le \operatorname{Cap}_1(A)+\varepsilon.
\end{align*}
\begin{align*}
\int_{{\mathbb R}^2} |\nabla u|\,d\mathcal L^2\le \operatorname{Cap}_1(A)+\varepsilon.
\end{align*} Here ![]() $u\in W^{1,1}({\mathbb R}^2)\subset \mathrm{BV}({\mathbb R}^2)$ with
$u\in W^{1,1}({\mathbb R}^2)\subset \mathrm{BV}({\mathbb R}^2)$ with  $|Du|({\mathbb R}^2)= \int_{{\mathbb R}^2} |\nabla u|\,d\mathcal L^2$, and then by the coarea formula (2.7) we find a set
$|Du|({\mathbb R}^2)= \int_{{\mathbb R}^2} |\nabla u|\,d\mathcal L^2$, and then by the coarea formula (2.7) we find a set ![]() $E:=\{u \gt t\}$ for some
$E:=\{u \gt t\}$ for some ![]() $0 \lt t \lt 1$, for which
$0 \lt t \lt 1$, for which
and A is contained in the interior of E. Then necessarily ![]() $|E| \lt \infty$, and for every
$|E| \lt \infty$, and for every ![]() $x\in A$ we find
$x\in A$ we find ![]() $r_x \gt 0$ such that
$r_x \gt 0$ such that
 \begin{align*}
\frac{|B(x,r_x)\cap E|}{|B(x,r_x)|}=\frac{1}{2}.
\end{align*}
\begin{align*}
\frac{|B(x,r_x)\cap E|}{|B(x,r_x)|}=\frac{1}{2}.
\end{align*}From the relative isoperimetric inequality (2.9), we get
 \begin{align*}
\frac{\pi r_x^2}{2}
=\min\{|B(x,r_x)\cap E|,|B(x,r_x)\setminus E|\}
\le r_x|D\chi_{E}|(B(x,r_x)).
\end{align*}
\begin{align*}
\frac{\pi r_x^2}{2}
=\min\{|B(x,r_x)\cap E|,|B(x,r_x)\setminus E|\}
\le r_x|D\chi_{E}|(B(x,r_x)).
\end{align*} In particular, the radii rx are uniformly bounded from above by ![]() $(2/\pi)|D\chi_E|({\mathbb R}^2)$. By the 5-covering theorem (see e.g. [Reference Heinonen, Koskela, Shanmugalingam and Tyson11, p. 60]), we can choose a finite or countable collection
$(2/\pi)|D\chi_E|({\mathbb R}^2)$. By the 5-covering theorem (see e.g. [Reference Heinonen, Koskela, Shanmugalingam and Tyson11, p. 60]), we can choose a finite or countable collection ![]() $\{B(x_j,r_j)\}_{j}$ of pairwise disjoint disks such that the disks
$\{B(x_j,r_j)\}_{j}$ of pairwise disjoint disks such that the disks ![]() $B(x_j,5r_j)$ cover A. Then
$B(x_j,5r_j)$ cover A. Then
 \begin{align*}
\mathcal H_{\infty}^1(A)
\le \sum_{j}10r_j
\le \frac{20}{\pi}\sum_{j}|D\chi_{E}|(B(x_j,r_j))
\le 10 |D\chi_{E}|({\mathbb R}^2)
\le 10(\operatorname{Cap}_1(A)+\varepsilon).
\end{align*}
\begin{align*}
\mathcal H_{\infty}^1(A)
\le \sum_{j}10r_j
\le \frac{20}{\pi}\sum_{j}|D\chi_{E}|(B(x_j,r_j))
\le 10 |D\chi_{E}|({\mathbb R}^2)
\le 10(\operatorname{Cap}_1(A)+\varepsilon).
\end{align*}Letting ɛ → 0, we get the result.
For ![]() $x\in{\mathbb R}^2$, let
$x\in{\mathbb R}^2$, let ![]() $p(x):=|x|$.
$p(x):=|x|$.
Lemma 4.6. Let ![]() $A\subset{\mathbb R}^2$. Then we have
$A\subset{\mathbb R}^2$. Then we have ![]() $\mathcal L^1(p(A))\le 10\operatorname{Cap}_1(A)$.
$\mathcal L^1(p(A))\le 10\operatorname{Cap}_1(A)$.
Proof. Note that p is a 1-Lipschitz function. Thus we estimate
by lemma 4.5.
The following theorem is a more general version of our main theorem 1.3. Note in particular that the function  $K_f^{\mathrm{fine}}$ is not generally known to be measurable; in theorem 1.3, measurability is an assumption implicitly contained in the fact that
$K_f^{\mathrm{fine}}$ is not generally known to be measurable; in theorem 1.3, measurability is an assumption implicitly contained in the fact that  $K_f^{\mathrm{fine}}\in L^{p^*/2}_{\mathrm{loc}}({\mathbb R}^n)$.
$K_f^{\mathrm{fine}}\in L^{p^*/2}_{\mathrm{loc}}({\mathbb R}^n)$.
Theorem 4.7. Let ![]() $\Omega,\Omega'\subset {\mathbb R}^2$ be open sets with
$\Omega,\Omega'\subset {\mathbb R}^2$ be open sets with ![]() $|\Omega'| \lt \infty$, and let
$|\Omega'| \lt \infty$, and let ![]() $f\colon \Omega\to \Omega'$ be a homeomorphism. Let
$f\colon \Omega\to \Omega'$ be a homeomorphism. Let ![]() $1\le p\le 2$. Suppose
$1\le p\le 2$. Suppose  $K_f^{\mathrm{fine}} \lt \infty$ outside a set
$K_f^{\mathrm{fine}} \lt \infty$ outside a set ![]() $E\subset \Omega$ such that for a.e. line L parallel to a coordinate axis,
$E\subset \Omega$ such that for a.e. line L parallel to a coordinate axis, ![]() $E\cap L$ is at most countable. Suppose also that there is
$E\cap L$ is at most countable. Suppose also that there is  $h\ge K_f^{\mathrm{fine}}$ such that
$h\ge K_f^{\mathrm{fine}}$ such that  $h\in L^{p^*/2}(\Omega)$. Then
$h\in L^{p^*/2}(\Omega)$. Then ![]() $f\in D^{p}(\Omega;{\mathbb R}^2)$, and in the case p = 2 we obtain that f is quasiconformal with
$f\in D^{p}(\Omega;{\mathbb R}^2)$, and in the case p = 2 we obtain that f is quasiconformal with  $K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e.
$K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e. ![]() $x\in\Omega$ and
$x\in\Omega$ and
 \begin{align}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{4}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align}
\begin{align}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{4}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align} Recall that here ![]() $D^p(\Omega;{\mathbb R}^2)$ is the Dirichlet space, that is, f is not necessarily in
$D^p(\Omega;{\mathbb R}^2)$ is the Dirichlet space, that is, f is not necessarily in ![]() $L^p(\Omega;{\mathbb R}^2)$, only in
$L^p(\Omega;{\mathbb R}^2)$, only in ![]() $L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^2)$.
$L^1_{\mathrm{loc}}(\Omega;{\mathbb R}^2)$.
Proof. We can assume that Ω is nonempty, and at first we also assume that Ω is bounded. The crux of the proof is to show D 1-regularity. For this, we use the fact that  $h\in L^{p^*/2}(\Omega)\subset L^1(\Omega)$. First, we assume also that h is lower semicontinuous.
$h\in L^{p^*/2}(\Omega)\subset L^1(\Omega)$. First, we assume also that h is lower semicontinuous.
Fix ![]() $0 \lt \varepsilon\le 1$. To every
$0 \lt \varepsilon\le 1$. To every ![]() $x\in\Omega\setminus E$, there corresponds a 1-finely open set
$x\in\Omega\setminus E$, there corresponds a 1-finely open set ![]() $U_x\ni x$ for which
$U_x\ni x$ for which
 \begin{align*}
\lim_{r\to 0}\frac{\operatorname{Cap}_1(B(x,r)\setminus U_{x})}{r}=0
\end{align*}
\begin{align*}
\lim_{r\to 0}\frac{\operatorname{Cap}_1(B(x,r)\setminus U_{x})}{r}=0
\end{align*}and
 \begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U_x)}{|f(B(x,r))|^{1/2}} \lt K_f^{\mathrm{fine}}(x)^{1/2}+\varepsilon.
\end{align*}
\begin{align*}
\limsup_{r\to 0}\frac{\operatorname{diam} f(B(x,r)\cap U_x)}{|f(B(x,r))|^{1/2}} \lt K_f^{\mathrm{fine}}(x)^{1/2}+\varepsilon.
\end{align*} For each ![]() $j\in {\mathbb N}$, let Aj consist of points
$j\in {\mathbb N}$, let Aj consist of points ![]() $x\in\Omega\setminus E$ for which
$x\in\Omega\setminus E$ for which
 \begin{align}
\sup_{0 \lt r\le 1/j}\frac{\operatorname{Cap}_1(B(x,r)\setminus U_{x})}{r} \lt \frac{1}{20}
\end{align}
\begin{align}
\sup_{0 \lt r\le 1/j}\frac{\operatorname{Cap}_1(B(x,r)\setminus U_{x})}{r} \lt \frac{1}{20}
\end{align}and
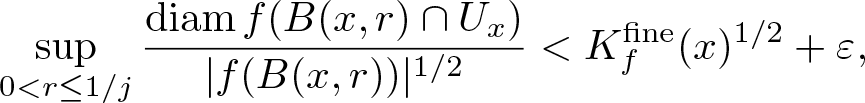 \begin{align}
\sup_{0 \lt r\le 1/j}\frac{\operatorname{diam} f(B(x,r)\cap U_x)}{|f(B(x,r))|^{1/2}} \lt K_f^{\mathrm{fine}}(x)^{1/2}+\varepsilon,
\end{align}
\begin{align}
\sup_{0 \lt r\le 1/j}\frac{\operatorname{diam} f(B(x,r)\cap U_x)}{|f(B(x,r))|^{1/2}} \lt K_f^{\mathrm{fine}}(x)^{1/2}+\varepsilon,
\end{align}and also (recall the lower semicontinuity of h)
 \begin{align}
K_f^{\mathrm{fine}}(x) \lt h(y)+\varepsilon\quad \textrm{for all }y\in B(x,1/j)\cap \Omega.
\end{align}
\begin{align}
K_f^{\mathrm{fine}}(x) \lt h(y)+\varepsilon\quad \textrm{for all }y\in B(x,1/j)\cap \Omega.
\end{align} We have  $\Omega=\bigcup_{j=1}^{\infty}A_j\cup E$. For
$\Omega=\bigcup_{j=1}^{\infty}A_j\cup E$. For ![]() $j=1,2\ldots$, we inductively define
$j=1,2\ldots$, we inductively define
 \begin{align*}
D_j:=\Omega\cap\overline{A_j\setminus \cup_{l=1}^{j-1}D_l} \setminus \bigcup_{l=1}^{j-1}D_l;
\end{align*}
\begin{align*}
D_j:=\Omega\cap\overline{A_j\setminus \cup_{l=1}^{j-1}D_l} \setminus \bigcup_{l=1}^{j-1}D_l;
\end{align*} note that we do not know the sets Aj to be measurable but the sets Dj are Borel sets. Moreover, the sets Dj are disjoint and  $D_j \supset A_j\setminus \bigcup_{l=1}^{j-1}D_l$, so that
$D_j \supset A_j\setminus \bigcup_{l=1}^{j-1}D_l$, so that  $\Omega= E\cup \bigcup_{j=1}^{\infty}D_j$. We can pick open sets
$\Omega= E\cup \bigcup_{j=1}^{\infty}D_j$. We can pick open sets ![]() $W_j\supset D_j$ such that
$W_j\supset D_j$ such that ![]() $W_j\subset \Omega$ and
$W_j\subset \Omega$ and
 \begin{align}
\int_{W_j}(h+2\varepsilon)\,d\mathcal L^2
\le \int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon
\end{align}
\begin{align}
\int_{W_j}(h+2\varepsilon)\,d\mathcal L^2
\le \int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon
\end{align}and such that
Fix R > 0. For each ![]() $k\in{\mathbb N}$, using lemma 4.4, we take a Whitney-type covering
$k\in{\mathbb N}$, using lemma 4.4, we take a Whitney-type covering
of  $A_{j}\setminus \bigcup_{l=1}^{j-1}D_l$ in Wj at scale
$A_{j}\setminus \bigcup_{l=1}^{j-1}D_l$ in Wj at scale ![]() $\min\{R,1/j\}$. By lemma 4.4(1), we know that
$\min\{R,1/j\}$. By lemma 4.4(1), we know that  $D_j\subset \bigcup_{k}\tfrac 12 B_{j,k}$ and so
$D_j\subset \bigcup_{k}\tfrac 12 B_{j,k}$ and so
 \begin{align}
\Omega\setminus E\subset \bigcup_{j,k}\tfrac 12 B_{j,k}.
\end{align}
\begin{align}
\Omega\setminus E\subset \bigcup_{j,k}\tfrac 12 B_{j,k}.
\end{align} For each point ![]() $x_{j,k}$, there is the corresponding 1-finely open set
$x_{j,k}$, there is the corresponding 1-finely open set  $U_{x_{j,k}}$. Denote
$U_{x_{j,k}}$. Denote  $U_{j,k}:= U_{x_{j,k}}\cap B_{j,k}$. For any
$U_{j,k}:= U_{x_{j,k}}\cap B_{j,k}$. For any ![]() $x\in{\mathbb R}^2$ and r > 0, denote a circle by
$x\in{\mathbb R}^2$ and r > 0, denote a circle by ![]() $S(x,r)$. From (4.9) and lemma 4.6, we obtain that there exists
$S(x,r)$. From (4.9) and lemma 4.6, we obtain that there exists ![]() $s_{j,k}\in (r_{j,k}/2,r_{j,k})$ such that
$s_{j,k}\in (r_{j,k}/2,r_{j,k})$ such that ![]() $S(x_{j,k},s_{j,k})\subset U_{j,k}$.
$S(x_{j,k},s_{j,k})\subset U_{j,k}$.
Define
 \begin{align*}
g:=2\sum_{j,k}
\frac{\operatorname{diam} f(U_{j,k}) }{r_{j,k}}\chi_{B_{j,k}}.
\end{align*}
\begin{align*}
g:=2\sum_{j,k}
\frac{\operatorname{diam} f(U_{j,k}) }{r_{j,k}}\chi_{B_{j,k}}.
\end{align*} By assumption, for almost every line L in the direction of a coordinate axis, ![]() $L\cap E$ is at most countable. Take a line segment
$L\cap E$ is at most countable. Take a line segment ![]() $\gamma\colon [0,\ell]\to L\cap \Omega$ in such a line L, with length
$\gamma\colon [0,\ell]\to L\cap \Omega$ in such a line L, with length ![]() $\ell \gt 0$. We denote also the image of γ by the same symbol. If
$\ell \gt 0$. We denote also the image of γ by the same symbol. If ![]() $\ell\ge R$, we have
$\ell\ge R$, we have
 \begin{align}
\int_\gamma g\,ds
\ge 2\sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\int_\gamma \frac{\operatorname{diam} f(U_{j,k}) }{r_{j,k}}\chi_{B_{j,k}}\,ds
\ge \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\operatorname{diam} f(U_{j,k}).
\end{align}
\begin{align}
\int_\gamma g\,ds
\ge 2\sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\int_\gamma \frac{\operatorname{diam} f(U_{j,k}) }{r_{j,k}}\chi_{B_{j,k}}\,ds
\ge \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\operatorname{diam} f(U_{j,k}).
\end{align}By (4.14), we have
 \begin{align*}
\gamma\setminus E \subset \bigcup_{j,k}\tfrac 12 B_{j,k}.
\end{align*}
\begin{align*}
\gamma\setminus E \subset \bigcup_{j,k}\tfrac 12 B_{j,k}.
\end{align*} Let ![]() $0 \lt \delta \lt R$. Since
$0 \lt \delta \lt R$. Since ![]() $L\cap E$ is at most countable, using the continuity of f we find a finite or countable collection of disks
$L\cap E$ is at most countable, using the continuity of f we find a finite or countable collection of disks ![]() $\{B_l\}$ intersecting
$\{B_l\}$ intersecting ![]() $\gamma\cap E$ such that
$\gamma\cap E$ such that ![]() $\overline{B_l}\subset \Omega$ and
$\overline{B_l}\subset \Omega$ and
 \begin{align*}
\gamma\cap E\subset \bigcup_l B_l
\quad\textrm{and}\quad
\sum_l \operatorname{diam} f(\overline{B_l}) \lt \delta.
\end{align*}
\begin{align*}
\gamma\cap E\subset \bigcup_l B_l
\quad\textrm{and}\quad
\sum_l \operatorname{diam} f(\overline{B_l}) \lt \delta.
\end{align*} Since the disks  $\tfrac 12 B_{j,k}$ and Bl are open, there is in fact a finite number of them covering γ. Thus, there are finite index sets I 1 and I 2 such that every disk
$\tfrac 12 B_{j,k}$ and Bl are open, there is in fact a finite number of them covering γ. Thus, there are finite index sets I 1 and I 2 such that every disk  $\tfrac 12 B_{j,k}$ with
$\tfrac 12 B_{j,k}$ with ![]() $(j,k)\in I_1$ intersects γ and
$(j,k)\in I_1$ intersects γ and
 \begin{align*}
\gamma
\subset \bigcup_{(j,k)\in I_1}\tfrac 12 B_{j,k}\cup \bigcup_{l\in I_2} B_l
\subset \bigcup_{(j,k)\in I_1} B(x_{j,k},s_{j,k})\cup \bigcup_{l\in I_2} B_l.
\end{align*}
\begin{align*}
\gamma
\subset \bigcup_{(j,k)\in I_1}\tfrac 12 B_{j,k}\cup \bigcup_{l\in I_2} B_l
\subset \bigcup_{(j,k)\in I_1} B(x_{j,k},s_{j,k})\cup \bigcup_{l\in I_2} B_l.
\end{align*} We find subsets ![]() $J_1\subset I_1$ and
$J_1\subset I_1$ and ![]() $J_2\subset I_2$ such that among the disks
$J_2\subset I_2$ such that among the disks ![]() $B(x_{j,k},s_{j,k})$,
$B(x_{j,k},s_{j,k})$, ![]() $(j,k)\in J_1$, Bl,
$(j,k)\in J_1$, Bl, ![]() $l\in J_2$, no disk is fully contained in another disk, and we still have
$l\in J_2$, no disk is fully contained in another disk, and we still have
 \begin{align*}
\gamma
\subset \bigcup_{(j,k)\in J_1}B(x_{j,k},s_{j,k})
\cup \bigcup_{l\in J_2} B_l.
\end{align*}
\begin{align*}
\gamma
\subset \bigcup_{(j,k)\in J_1}B(x_{j,k},s_{j,k})
\cup \bigcup_{l\in J_2} B_l.
\end{align*} Relabel the disks ![]() $B(x_{j,k},s_{j,k})$,
$B(x_{j,k},s_{j,k})$, ![]() $(j,k)\in J_1$, and Bl,
$(j,k)\in J_1$, and Bl, ![]() $l\in J_2$, as
$l\in J_2$, as ![]() $B(y_1,r_1),\ldots,B(y_M,r_M)$. We can assume that γ is in the x 2-coordinate direction. Denote by zm the x 2-coordinate of the point in
$B(y_1,r_1),\ldots,B(y_M,r_M)$. We can assume that γ is in the x 2-coordinate direction. Denote by zm the x 2-coordinate of the point in ![]() $\gamma\cap \overline{B}(y_m,r_m)$ with the smallest x 2-coordinate. We can assume that the disks
$\gamma\cap \overline{B}(y_m,r_m)$ with the smallest x 2-coordinate. We can assume that the disks ![]() $B(y_1,r_1),\ldots,B(y_M,r_M)$ are ordered such that
$B(y_1,r_1),\ldots,B(y_M,r_M)$ are ordered such that ![]() $z_1\le \cdots \le z_M$. Since these disks cover γ, for each
$z_1\le \cdots \le z_M$. Since these disks cover γ, for each ![]() $m=1,\ldots,M-1$ we have that
$m=1,\ldots,M-1$ we have that ![]() $\overline{B}(y_{m+1},r_{m+1})$ necessarily intersects
$\overline{B}(y_{m+1},r_{m+1})$ necessarily intersects ![]() $\bigcup_{m'=1}^m\overline{B}(y_{m'},r_{m'})\cap \gamma$, and since none of the disks
$\bigcup_{m'=1}^m\overline{B}(y_{m'},r_{m'})\cap \gamma$, and since none of the disks ![]() $\overline{B}(y_{m'},r_{m'})$,
$\overline{B}(y_{m'},r_{m'})$, ![]() $m'\in\{1,\ldots,M\}$ is contained in another one, in fact
$m'\in\{1,\ldots,M\}$ is contained in another one, in fact ![]() $S(y_{m+1},r_{m+1})$ necessarily intersects
$S(y_{m+1},r_{m+1})$ necessarily intersects ![]() $\bigcup_{m'=1}^m S(y_{m'},r_{m'})$. In total,
$\bigcup_{m'=1}^m S(y_{m'},r_{m'})$. In total,  $\bigcup_{m=1}^M S(y_{m},r_{m})$ is a connected set. It follows that
$\bigcup_{m=1}^M S(y_{m},r_{m})$ is a connected set. It follows that
 \begin{align}
\operatorname{diam}\left(\left(\bigcup_{m=1}^{M}f(S(y_m,r_m))\right)\right)
\le \sum_{m=1}^{M}\operatorname{diam} f(S(y_m,r_m)).
\end{align}
\begin{align}
\operatorname{diam}\left(\left(\bigcup_{m=1}^{M}f(S(y_m,r_m))\right)\right)
\le \sum_{m=1}^{M}\operatorname{diam} f(S(y_m,r_m)).
\end{align}Denote by ω a modulus of continuity of f at the end points of the line segment γ. Then
 \begin{align*}
|f(\gamma(0))-f(\gamma(\ell))|
&\le \operatorname{diam}\left(\left(\bigcup_{m=1}^{M}f(S(y_m,r_m))\right)\right)+2\omega(R)\\
&\le \sum_{m=1}^M\operatorname{diam} f(S(y_m,r_m))+2\omega(R)
\quad\textrm{by (4.16)}\\
&\le \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}
\operatorname{diam} f(S(x_{j,k},s_{j,k}))+\sum_l \operatorname{diam} f(\overline{B_l})+2\omega(R)\\
&\le \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\operatorname{diam} f(U_{j,k})+\sum_l \operatorname{diam} f(\overline{B_l})+2\omega(R)\\
&\le \int_\gamma g\,ds +\delta+2\omega(R)
\quad\textrm{by (4.15)}.
\end{align*}
\begin{align*}
|f(\gamma(0))-f(\gamma(\ell))|
&\le \operatorname{diam}\left(\left(\bigcup_{m=1}^{M}f(S(y_m,r_m))\right)\right)+2\omega(R)\\
&\le \sum_{m=1}^M\operatorname{diam} f(S(y_m,r_m))+2\omega(R)
\quad\textrm{by (4.16)}\\
&\le \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}
\operatorname{diam} f(S(x_{j,k},s_{j,k}))+\sum_l \operatorname{diam} f(\overline{B_l})+2\omega(R)\\
&\le \sum_{j,k,\,\gamma\cap \tfrac 12 B_{j,k}\neq \emptyset}\operatorname{diam} f(U_{j,k})+\sum_l \operatorname{diam} f(\overline{B_l})+2\omega(R)\\
&\le \int_\gamma g\,ds +\delta+2\omega(R)
\quad\textrm{by (4.15)}.
\end{align*}Letting δ → 0, we get
 \begin{align}
|f(\gamma(0))-f(\gamma(\ell))|
\le \int_\gamma g\,ds +2\omega(R).
\end{align}
\begin{align}
|f(\gamma(0))-f(\gamma(\ell))|
\le \int_\gamma g\,ds +2\omega(R).
\end{align} By Young’s inequality, we have for any ![]() $b_1,b_2\ge 0$ and
$b_1,b_2\ge 0$ and ![]() $0 \lt \kappa\le 1$ that
$0 \lt \kappa\le 1$ that
 \begin{align}
\begin{split}
b_1b_2=\kappa^{1/2} b_1 \kappa^{-1/2} b_2
&\le \frac{1}{2}\kappa b_1^2 + \frac{1}{2}\kappa^{-1} b_2^{2}.
\end{split}
\end{align}
\begin{align}
\begin{split}
b_1b_2=\kappa^{1/2} b_1 \kappa^{-1/2} b_2
&\le \frac{1}{2}\kappa b_1^2 + \frac{1}{2}\kappa^{-1} b_2^{2}.
\end{split}
\end{align} For every ![]() $j\in{\mathbb N}$, we estimate
$j\in{\mathbb N}$, we estimate
 \begin{align*}
2\pi^{-1}\sum_{k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} | B_{j,k}|
& \le 2\sum_{k}\operatorname{diam} f(U_{j,k})r_{j,k}\\
& \le 2\sum_{k} |f(B_{j,k})|^{1/2}
\left(K_f^{\mathrm{fine}}(x_{j,k})^{1/2}+\varepsilon\right)r_{j,k}
\quad\textrm{by (4.10)}\\
& \le\kappa\sum_{k} |f(B_{j,k})|
+2\kappa^{-1}\sum_{k} (K_f^{\mathrm{fine}}(x_{j,k})+\varepsilon)r_{j,k}^{2}
\quad\textrm{by (4.18)}.
\end{align*}
\begin{align*}
2\pi^{-1}\sum_{k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} | B_{j,k}|
& \le 2\sum_{k}\operatorname{diam} f(U_{j,k})r_{j,k}\\
& \le 2\sum_{k} |f(B_{j,k})|^{1/2}
\left(K_f^{\mathrm{fine}}(x_{j,k})^{1/2}+\varepsilon\right)r_{j,k}
\quad\textrm{by (4.10)}\\
& \le\kappa\sum_{k} |f(B_{j,k})|
+2\kappa^{-1}\sum_{k} (K_f^{\mathrm{fine}}(x_{j,k})+\varepsilon)r_{j,k}^{2}
\quad\textrm{by (4.18)}.
\end{align*}Using (4.11), we estimate further
 \begin{align*}
&2\pi^{-1} \sum_{k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} | B_{j,k}|\\
&\ \le \kappa\sum_{k} |f(B_{j,k})|+
2 \kappa^{-1}\sum_{k} \int_{B_{j,k}}(h+2\varepsilon)\,d\mathcal L^2\\
&\ \le 6400 \kappa |f(W_j)|\quad\textrm{by lemma 4.4}(3)\,\textrm{and injectivity}\\
&\qquad +
12800 \kappa^{-1} \int_{W_{j}}(h+2\varepsilon)\,d\mathcal L^2
\quad \textrm{by lemma 4.4}(3)\\
&\ \le 6400\kappa (|f(D_j)|+2^{-j}\varepsilon)+\\
&\qquad +12800 \kappa^{-1}
\left(\int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon\right)
\quad\textrm{by (4.12) and (4.13)}.
\end{align*}
\begin{align*}
&2\pi^{-1} \sum_{k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} | B_{j,k}|\\
&\ \le \kappa\sum_{k} |f(B_{j,k})|+
2 \kappa^{-1}\sum_{k} \int_{B_{j,k}}(h+2\varepsilon)\,d\mathcal L^2\\
&\ \le 6400 \kappa |f(W_j)|\quad\textrm{by lemma 4.4}(3)\,\textrm{and injectivity}\\
&\qquad +
12800 \kappa^{-1} \int_{W_{j}}(h+2\varepsilon)\,d\mathcal L^2
\quad \textrm{by lemma 4.4}(3)\\
&\ \le 6400\kappa (|f(D_j)|+2^{-j}\varepsilon)+\\
&\qquad +12800 \kappa^{-1}
\left(\int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon\right)
\quad\textrm{by (4.12) and (4.13)}.
\end{align*} It follows that for every ![]() $j\in{\mathbb N}$,
$j\in{\mathbb N}$,
 \begin{align}
\begin{split}
\pi^{-1}\int_{\Omega}g\,d\mathcal L^2
&= 2\pi^{-1}\sum_{j,k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} \mathcal |B_{j,k}|\\
&\le 6400\kappa \sum_{j=1}^{\infty}(|f(D_j)|+2^{-j}\varepsilon)+\\
&\qquad +12800 \kappa^{-1}
\sum_{j=1}^{\infty}\left(\int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon\right)\\
& \le 6400\kappa (|f(\Omega)|+\varepsilon)
+ 12800\kappa^{-1} \left(\int_{\Omega}(h+2\varepsilon)\,d\mathcal L^2+\varepsilon\right)\\
& \le 6400\kappa |f(\Omega)| +12800\kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2
+19200\kappa^{-1}\varepsilon.
\end{split}
\end{align}
\begin{align}
\begin{split}
\pi^{-1}\int_{\Omega}g\,d\mathcal L^2
&= 2\pi^{-1}\sum_{j,k}\frac{\operatorname{diam} f(U_{j,k})}{r_{j,k}} \mathcal |B_{j,k}|\\
&\le 6400\kappa \sum_{j=1}^{\infty}(|f(D_j)|+2^{-j}\varepsilon)+\\
&\qquad +12800 \kappa^{-1}
\sum_{j=1}^{\infty}\left(\int_{D_j}(h+2\varepsilon)\,d\mathcal L^2+2^{-j}\varepsilon\right)\\
& \le 6400\kappa (|f(\Omega)|+\varepsilon)
+ 12800\kappa^{-1} \left(\int_{\Omega}(h+2\varepsilon)\,d\mathcal L^2+\varepsilon\right)\\
& \le 6400\kappa |f(\Omega)| +12800\kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2
+19200\kappa^{-1}\varepsilon.
\end{split}
\end{align} We can pick functions g as above, with the choices ![]() $R=1/i$, to obtain a sequence
$R=1/i$, to obtain a sequence ![]() $\{g_i\}_{i=1}^{\infty}$. Recall the definition of pointwise variation from (2.11), as well as (2.12). By (4.17), for
$\{g_i\}_{i=1}^{\infty}$. Recall the definition of pointwise variation from (2.11), as well as (2.12). By (4.17), for ![]() $\mathcal L^{1}$-a.e.
$\mathcal L^{1}$-a.e. ![]() $z\in\pi_2(\Omega)$, we get for any line segment
$z\in\pi_2(\Omega)$, we get for any line segment ![]() $\gamma\colon [0,\ell]\to \Omega$ with
$\gamma\colon [0,\ell]\to \Omega$ with ![]() $\gamma(s):=(z,t+s)$ for some
$\gamma(s):=(z,t+s)$ for some ![]() $t\in{\mathbb R}$ that
$t\in{\mathbb R}$ that
 \begin{align*}
|f(\gamma(0))-f(\gamma(\ell))|\le \liminf_{i\to\infty}\left(\int_{\gamma} g_i\,ds+2\omega(1/i)\right)
=\liminf_{i\to\infty}\int_{\gamma} g_i\,ds,
\end{align*}
\begin{align*}
|f(\gamma(0))-f(\gamma(\ell))|\le \liminf_{i\to\infty}\left(\int_{\gamma} g_i\,ds+2\omega(1/i)\right)
=\liminf_{i\to\infty}\int_{\gamma} g_i\,ds,
\end{align*}and so
 \begin{align*}
\operatorname{pV}(f_z,\Omega_z)
\le \liminf_{i\to\infty}\int_{\Omega_z} g_i\,ds.
\end{align*}
\begin{align*}
\operatorname{pV}(f_z,\Omega_z)
\le \liminf_{i\to\infty}\int_{\Omega_z} g_i\,ds.
\end{align*}We estimate
 \begin{align*}
&\int_{\pi_2(\Omega)}\operatorname{pV}(f_z,\Omega_z)\,d\mathcal L^{1}(z)\\
&\qquad \le \int_{\pi_2(\Omega)}\liminf_{i\to\infty}\int_{\Omega_z} g_i\,ds\,d\mathcal L^{1}(z)\\
&\qquad \le \liminf_{i\to\infty}\int_{\pi_2(\Omega)}\int_{\Omega_z} g_i\,ds\,d\mathcal L^{1}(z)
\quad\textrm{by Fatou's lemma}\\
&\qquad = \liminf_{i\to\infty}\int_{\Omega} g_i\,d\mathcal L^{2}\quad\textrm{by Fubini}\\
&\qquad \le 6400 \pi \kappa |f(\Omega)| +12800 \pi \kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2
+19200 \pi \kappa^{-1} \varepsilon
\quad\textrm{by (4.19)}.
\end{align*}
\begin{align*}
&\int_{\pi_2(\Omega)}\operatorname{pV}(f_z,\Omega_z)\,d\mathcal L^{1}(z)\\
&\qquad \le \int_{\pi_2(\Omega)}\liminf_{i\to\infty}\int_{\Omega_z} g_i\,ds\,d\mathcal L^{1}(z)\\
&\qquad \le \liminf_{i\to\infty}\int_{\pi_2(\Omega)}\int_{\Omega_z} g_i\,ds\,d\mathcal L^{1}(z)
\quad\textrm{by Fatou's lemma}\\
&\qquad = \liminf_{i\to\infty}\int_{\Omega} g_i\,d\mathcal L^{2}\quad\textrm{by Fubini}\\
&\qquad \le 6400 \pi \kappa |f(\Omega)| +12800 \pi \kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2
+19200 \pi \kappa^{-1} \varepsilon
\quad\textrm{by (4.19)}.
\end{align*}Recall (2.13). Since we can do the above calculation also in the x 1-coordinate direction, we obtain
 \begin{align*}
\operatorname{Var}(f,\Omega) \le 12800\pi\kappa |f(\Omega)|
+25600\pi \kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2+38400 \pi\kappa^{-1} \varepsilon.
\end{align*}
\begin{align*}
\operatorname{Var}(f,\Omega) \le 12800\pi\kappa |f(\Omega)|
+25600\pi \kappa^{-1}\int_{\Omega} (h+2\varepsilon) \,d\mathcal L^2+38400 \pi\kappa^{-1} \varepsilon.
\end{align*}Letting ɛ → 0, we get the estimate
 \begin{align*}
\operatorname{Var}(f,\Omega)\le 25600\pi \left(\kappa |f(\Omega)| +\kappa^{-1}\int_{\Omega}h\,d\mathcal L^2\right) \lt \infty.
\end{align*}
\begin{align*}
\operatorname{Var}(f,\Omega)\le 25600\pi \left(\kappa |f(\Omega)| +\kappa^{-1}\int_{\Omega}h\,d\mathcal L^2\right) \lt \infty.
\end{align*} All of the reasoning so far can be done also in every open subset ![]() $W\subset\Omega$, and so we have in fact
$W\subset\Omega$, and so we have in fact
 \begin{align*}
|Df|(W)\le 25600\pi \left(\kappa |f(W)| +\kappa^{-1}\int_{W}h\,d\mathcal L^2\right).
\end{align*}
\begin{align*}
|Df|(W)\le 25600\pi \left(\kappa |f(W)| +\kappa^{-1}\int_{W}h\,d\mathcal L^2\right).
\end{align*} By considering small κ > 0, we find that ![]() $|Df|$ is absolutely continuous with respect to
$|Df|$ is absolutely continuous with respect to ![]() $\mathcal L^2$ in Ω. Thus we get
$\mathcal L^2$ in Ω. Thus we get ![]() $f\in D^1(\Omega;{\mathbb R}^2)$, and choosing κ = 1, we get the estimate
$f\in D^1(\Omega;{\mathbb R}^2)$, and choosing κ = 1, we get the estimate
 \begin{align*}
\int_{\Omega}|\nabla f|\,d\mathcal L^2
\le 25600\pi\left( |f(\Omega)| +\int_{\Omega} h \,d\mathcal L^2\right).
\end{align*}
\begin{align*}
\int_{\Omega}|\nabla f|\,d\mathcal L^2
\le 25600\pi\left( |f(\Omega)| +\int_{\Omega} h \,d\mathcal L^2\right).
\end{align*} Now we remove the assumption that h is lower semicontinuous. Using the Vitali–Carathéodory theorem (theorem 2.5), we find a sequence ![]() $\{h_i\}_{i=1}^{\infty}$ of lower semicontinuous functions in
$\{h_i\}_{i=1}^{\infty}$ of lower semicontinuous functions in ![]() $L^1(\Omega)$ such that
$L^1(\Omega)$ such that ![]() $h\le h_{i+1}\le h_i$ for all
$h\le h_{i+1}\le h_i$ for all ![]() $i\in{\mathbb N}$, and
$i\in{\mathbb N}$, and ![]() $h_i\to h$ in
$h_i\to h$ in ![]() $L^1(\Omega)$. Thus, we get
$L^1(\Omega)$. Thus, we get
 \begin{align}
\int_{\Omega}|\nabla f|\,d\mathcal L^2
\le \liminf_{i\to\infty}25600\pi\left( |f(\Omega)| +\int_{\Omega} h_i \,d\mathcal L^2\right)
\le 25600\pi\left( |f(\Omega)| +\int_{\Omega} h \,d\mathcal L^2\right).
\end{align}
\begin{align}
\int_{\Omega}|\nabla f|\,d\mathcal L^2
\le \liminf_{i\to\infty}25600\pi\left( |f(\Omega)| +\int_{\Omega} h_i \,d\mathcal L^2\right)
\le 25600\pi\left( |f(\Omega)| +\int_{\Omega} h \,d\mathcal L^2\right).
\end{align} Now we prove that in fact ![]() $f\in D^p(\Omega;{\mathbb R}^2)$. Note that
$f\in D^p(\Omega;{\mathbb R}^2)$. Note that  $K_f^{\mathrm{fine}} \lt \infty$ a.e. in Ω. Since
$K_f^{\mathrm{fine}} \lt \infty$ a.e. in Ω. Since  $f\in D^1(\Omega,\Omega')\subset W_{\mathrm{loc}}^{1,1}(\Omega;\Omega')$, by proposition 4.3, we have
$f\in D^1(\Omega,\Omega')\subset W_{\mathrm{loc}}^{1,1}(\Omega;\Omega')$, by proposition 4.3, we have
 \begin{align}
K_f^{\mathrm{fine}}(x)^{1/2}J_f(x)^{1/2}
=\frac{2}{\pi^{1/2}}\Vert \nabla f(x)\Vert
\quad \textrm{for a.e. }x\in \Omega.
\end{align}
\begin{align}
K_f^{\mathrm{fine}}(x)^{1/2}J_f(x)^{1/2}
=\frac{2}{\pi^{1/2}}\Vert \nabla f(x)\Vert
\quad \textrm{for a.e. }x\in \Omega.
\end{align} In the case ![]() $1 \lt p \lt 2$, by Young’s inequality, and recalling that
$1 \lt p \lt 2$, by Young’s inequality, and recalling that  $h\ge K_f^{\mathrm{fine}}$, we get
$h\ge K_f^{\mathrm{fine}}$, we get
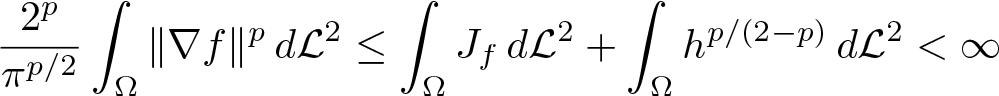 \begin{align}
\frac{2^p}{\pi^{p/2}}\int_{\Omega} \Vert \nabla f\Vert ^p\,d\mathcal L^2
\le \int_{\Omega} J_f\,d\mathcal L^2 + \int_{\Omega} h^{p/(2-p)}\,d\mathcal L^2 \lt \infty
\end{align}
\begin{align}
\frac{2^p}{\pi^{p/2}}\int_{\Omega} \Vert \nabla f\Vert ^p\,d\mathcal L^2
\le \int_{\Omega} J_f\,d\mathcal L^2 + \int_{\Omega} h^{p/(2-p)}\,d\mathcal L^2 \lt \infty
\end{align} by (2.2) and by the assumption  $h\in L^{p^*/2}(\Omega)$. Thus
$h\in L^{p^*/2}(\Omega)$. Thus ![]() $f\in D^p(\Omega;{\mathbb R}^2)$.
$f\in D^p(\Omega;{\mathbb R}^2)$.
In the case p = 2, we have  $K_f^{\mathrm{fine}}\le h\in L^{\infty}(\Omega)$, and then from (4.21) we get
$K_f^{\mathrm{fine}}\le h\in L^{\infty}(\Omega)$, and then from (4.21) we get
 \begin{align}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{4}\Vert h\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align}
\begin{align}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{4}\Vert h\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align} This shows that ![]() $f\in D^{2}(\Omega;\Omega')$. By definition 2.3 and the discussion below it, we then have that in fact f is quasiconformal; note that
$f\in D^{2}(\Omega;\Omega')$. By definition 2.3 and the discussion below it, we then have that in fact f is quasiconformal; note that ![]() $\nabla f(x)$ is now a classical gradient for a.e.
$\nabla f(x)$ is now a classical gradient for a.e. ![]() $x\in\Omega$. Moreover, using, e.g., [Reference Heinonen, Koskela, Shanmugalingam and Tyson10, theorem 9.8], we know that f −1 is also quasiconformal and thus absolutely continuous in measure, and so
$x\in\Omega$. Moreover, using, e.g., [Reference Heinonen, Koskela, Shanmugalingam and Tyson10, theorem 9.8], we know that f −1 is also quasiconformal and thus absolutely continuous in measure, and so ![]() $J_f(x) \gt 0$ for a.e.
$J_f(x) \gt 0$ for a.e. ![]() $x\in \Omega$. Thus by proposition 4.3, we have
$x\in \Omega$. Thus by proposition 4.3, we have  $K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e.
$K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e. ![]() $x\in\Omega$, and from (4.23) we obtain that (4.8) holds.
$x\in\Omega$, and from (4.23) we obtain that (4.8) holds.
Finally, using the Dirichlet energy estimates (4.20), (4.22), and (4.23), it is easy to generalize to the case where Ω is unbounded.
Proof of theorem 1.3
For every direction ![]() $v\in \partial B(0,1)$, the intersection of E with almost every line L parallel to v is at most countable, see e.g. [Reference Väisälä21, p. 103]. For every bounded open set
$v\in \partial B(0,1)$, the intersection of E with almost every line L parallel to v is at most countable, see e.g. [Reference Väisälä21, p. 103]. For every bounded open set ![]() $\Omega\subset {\mathbb R}^2$, we have
$\Omega\subset {\mathbb R}^2$, we have ![]() $|f(\Omega)| \lt \infty$ since f is a homeomorphism, and then by theorem 4.7, we have
$|f(\Omega)| \lt \infty$ since f is a homeomorphism, and then by theorem 4.7, we have ![]() $f\in D^p(\Omega;{\mathbb R}^2)$, and in the case p = 2, moreover
$f\in D^p(\Omega;{\mathbb R}^2)$, and in the case p = 2, moreover  $K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e.
$K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e. ![]() $x\in\Omega$ and
$x\in\Omega$ and
 \begin{align*}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{2}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align*}
\begin{align*}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{2}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}(\Omega)}J_f(x)
\quad \textrm{for a.e. }x\in \Omega.
\end{align*} Thus  $f\in W^{1,p}_{\mathrm{loc}}({\mathbb R}^2;{\mathbb R}^2)$, and in the case p = 2, we have
$f\in W^{1,p}_{\mathrm{loc}}({\mathbb R}^2;{\mathbb R}^2)$, and in the case p = 2, we have  $K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e.
$K_f(x)=K_f^{\mathrm{fine}}(x)$ for a.e. ![]() $x\in{\mathbb R}^2$ and
$x\in{\mathbb R}^2$ and
 \begin{align*}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{2}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}({\mathbb R}^n)}J_f(x)
\quad \textrm{for a.e. }x\in {\mathbb R}^2.
\end{align*}
\begin{align*}
\Vert \nabla f(x)\Vert ^2
\le \frac{\pi}{2}\Vert K_f^{\mathrm{fine}}\Vert_{L^{\infty}({\mathbb R}^n)}J_f(x)
\quad \textrm{for a.e. }x\in {\mathbb R}^2.
\end{align*} Thus f is quasiconformal in ![]() ${\mathbb R}^2$.
${\mathbb R}^2$.
Proof of corollary 1.4
This follows immediately from theorem 1.3.
In closing, we note that certain open problems arise naturally from our work. Koskela–Rogovin [Reference Koskela and Rogovin15, corollary 1.3] prove that in the definition of Kf, one can replace ‘![]() $\limsup$’ by ‘
$\limsup$’ by ‘![]() $\liminf$’, and the result (analogous to theorem 1.3) still holds. Thus one can ask: does theorem 1.3 still hold if ‘
$\liminf$’, and the result (analogous to theorem 1.3) still holds. Thus one can ask: does theorem 1.3 still hold if ‘![]() $\limsup$’ is replaced by ‘
$\limsup$’ is replaced by ‘![]() $\liminf$’ in the definition of
$\liminf$’ in the definition of  $K_f^{\mathrm{fine}}$?
$K_f^{\mathrm{fine}}$?
The assumption n = 2 was needed on page 18 to ensure that suitable circles are contained in the relevant 1-finely open sets; these circles could then be seen to intersect each other on page 19. In higher dimensions, it is not necessarily true that similar spheres would be contained in the 1-finely open sets. One can ask: can our results be generalized to ![]() ${\mathbb R}^n$ with
${\mathbb R}^n$ with ![]() $n\ge 3$, and further to metric measure spaces? Much of the literature on the topic, discussed in §1, in fact deals with the setting of quite general metric measure spaces. We observe that most of the quantities and techniques used in the proof of theorem 1.3 make sense also in metric spaces.
$n\ge 3$, and further to metric measure spaces? Much of the literature on the topic, discussed in §1, in fact deals with the setting of quite general metric measure spaces. We observe that most of the quantities and techniques used in the proof of theorem 1.3 make sense also in metric spaces.