1 results
RAMANUJAN SERIES UPSIDE-DOWN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 07 July 2014, pp. 78-106
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
-
We prove that there is a correspondence between Ramanujan-type formulas for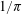
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1/\pi $ and formulas for Dirichlet 
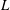$L$-values. Our method also allows us to reduce certain values of the Epstein zeta function to rapidly converging hypergeometric functions. The Epstein zeta functions were previously studied by Glasser and Zucker.
