Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T11:23:00.975Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMANUJAN SERIES UPSIDE-DOWN

Part of: Other special functions Computational number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 July 2014

JESUS GUILLERA  and
MATHEW ROGERS
JESUS GUILLERA
Affiliation:
Av. Cesáreo Alierta, 31 esc. izda 4°–A, Zaragoza, Spain email jguillera@gmail.com
MATHEW ROGERS*
Affiliation:
Department of Mathematics and Statistics, Université de Montréal, CP 6128 succ. Centre-ville, Montréal Québec H3C 3J7,Canada email mathewrogers@gmail.com
*
✉mathewrogers@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that there is a correspondence between Ramanujan-type formulas for 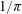$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1/\pi $ and formulas for Dirichlet 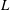$L$-values. Our method also allows us to reduce certain values of the Epstein zeta function to rapidly converging hypergeometric functions. The Epstein zeta functions were previously studied by Glasser and Zucker.

Keywords

Dirichlet L-valuesformulas for πhypergeometric serieslattice sumsRamanujan

MSC classification

Secondary: 33C20: Generalized hypergeometric series, $_pF_q$ 11F11: Holomorphic modular forms of integral weight 11F03: Modular and automorphic functions 11Y60: Evaluation of constants 33C75: Elliptic integrals as hypergeometric functions 33E05: Elliptic functions and integrals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 1 , August 2014 , pp. 78 - 106
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Apéry, R., ‘Irrationalité de ζ (2) et ζ (3)’, Astérisque 61 (1979), 11–13.Google Scholar
Baruah, N. D. and Berndt, B. C., ‘Ramanujan’s series for 1∕π arising from his cubic and quartic theories of elliptic functions’, J. Math. Anal. Appl. 341 (2008), 357–371.CrossRefGoogle Scholar
Bauer, G., ‘Von den Coefficienten der Reihen von Kugelfunctionen einer Variabeln’, J. reine angew. Math. 56 (1859), 101–121.Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part V (Springer, New York, 1998).CrossRefGoogle Scholar
Borwein, J. M. and Borwein, P. B., Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity (Wiley, New York, 1987).Google Scholar
Chan, H. H. and Cooper, S., ‘Rational analogues of Ramanujan’s formulas for 1∕π’, Math. Proc. Camb. Phil. Soc. 153 (2012), 361–383.CrossRefGoogle Scholar
Chudnovsky, D. B. and Chudnovsky, G. V., ‘Approximations and complex multiplication according to Ramanujan’, in: Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, 1–5 June, 1987 (eds. Andrews, G. E., Berndt, B. C. and Rankin, R. A.) (Academic Press, Boston, MA, 1987), 375–472.Google Scholar
Duke, W., ‘Some entries in Ramanujan’s notebooks’, Proc. Camb. Phil. Soc. 144 (2008), 255–266.Google Scholar
Glasser, M. L. and Zucker, I. J., ‘Lattice sums’, in: Theoretical Chemistry: Advances and Perspectives, Vol. 5 (eds. Eyring, H. and Henderson, D.) (1980), 67–139.CrossRefGoogle Scholar
Guillera, J., ‘Series de Ramanujan (Generalizaciones y conjecturas)’, PhD Thesis, Universidad de Zaragoza, Spain, 2007.Google Scholar
Guillera, J., ‘Hypergeometric identities for 10 extended Ramanujan-type series’, Ramanujan J. 15 (2008), 219–234.CrossRefGoogle Scholar
Guillera, J., ‘A matrix form of Ramanujan-type series for 1∕π’, in: Gems in Experimental Mathematics, AMS Special Session on Experimental Mathematics, Washington, DC, 5 January 2009, Contemporary Mathematics, 517 (eds. Amdeberhan, T., Medina, L. A. and Moll, V. H.) (American Mathematical Society, Providence, RI, 2010), 189–206.Google Scholar
Guillera, J., ‘WZ-proofs of “divergent” Ramanujan-type series’, in: Advances in Combinatorics (eds. Kotsireas, I. S. and Zima, E. V.) (Springer, Berlin, 2013), 187–195.CrossRefGoogle Scholar
Hessami Pilehrood, Kh. and Hessami Pilehrood, T., ‘Bivariate identities for values of the Hurwitz zeta function and supercongruences’, Electron. J. Combin. 18 (2012), 35–65.CrossRefGoogle Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds.) NIST Handbook of Mathematical Functions (Cambridge University Press, New York, 2010).Google Scholar
Ramanujan, S., ‘Modular equations and approximations to π [Quart. J. Math. 45 (1914), 350–372]’, in: Collected papers of Srinivasa Ramanujan 23–29, AMS Chelsea Publishing Series, 159 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Sun, Z.-W., ‘List of conjectural formulas for powers of $\pi $ and other constants’, arXiv:1102.5649.Google Scholar
Yang, Y., ‘Apéry limits and special values of L-functions’, J. Math. Anal. Appl. 343(1) (2008), 492–513.CrossRefGoogle Scholar
Zagier, D. and Gangl, H., ‘Classical and elliptic polylogarithms and special values of L-series’, in: Proceedings of the NATO Advanced Study Institute on The Arithmetic and Geometry of Algebraic Cycles, Banff, Alberta, Canada 7–19 June 1998, NATO Science Series C, Mathematical and Physical Sciences, 158 (eds. Gordon, B. B., Lewis, J. D., Müller-Stach, S., Saito, S. and Yui, N.) (Kluwer Academic, Dordrecht, The Netherlands, 2000), 561–615.Google Scholar
Zeilberger, D., ‘Closed form (pun intended!)’, Contemp. Math. 143 (1993), 579–608.CrossRefGoogle Scholar
Zucker, I. J. and McPhedran, R. C., ‘Dirichlet L-series with real and complex characters and their application to solving double sums’, Proc. R. Soc. A 464 (2008), 1405–1422.CrossRefGoogle Scholar
Zucker, I. J. and Robertson, M. M., ‘Further aspects of the evaluation of ∑(m, n≠0, 0(a m 2 + b n m + c n 2)−s’, Math. Proc. Camb. Phil. Soc. 95 (1984), 5–13.CrossRefGoogle Scholar