The two problem, both raised in the literature, are: (I) Is there, amongst all the permutational products (p.p.s.) on the amalgam 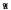 = (A, B; H) at least one which is a minimal generalized regular product? (II) If one of the p.p.s. on
= (A, B; H) at least one which is a minimal generalized regular product? (II) If one of the p.p.s. on 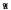 is isomorphic to the generalized free product (g.f.p.) F on U are they all? We answer both of them negatively.
is isomorphic to the generalized free product (g.f.p.) F on U are they all? We answer both of them negatively.