Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T17:09:43.316Z Has data issue: false hasContentIssue false
  • English
  • Français

The solutions to two problems on permutational products

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

R. B. J. T. Allenby
R. B. J. T. Allenby
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The two problem, both raised in the literature, are: (I) Is there, amongst all the permutational products (p.p.s.) on the amalgam 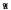= (A, B; H) at least one which is a minimal generalized regular product? (II) If one of the p.p.s. on 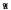is isomorphic to the generalized free product (g.f.p.) F on U are they all? We answer both of them negatively.

Keywords

generalized free productgeneralized regular productfree nilpotent grouppermutational productfree group

MSC classification

Secondary: 20E22: Extensions, wreath products, and other compositions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 4 , December 1981 , pp. 390 - 394
Copyright
Copyright © Australian Mathematical Society 1981

References

Allenby, R. B. J. T. (1969), ‘Permutational products and regular products of groups’, Trans. Amer. Math. Soc. 136, 537–543.CrossRefGoogle Scholar
Allenby, R. B. J. T. and Tang, C. Y. (1975), ‘On the Frattini subgroups of generalized free products and the embedding of amalgams’, Trans. Amer. Math. Soc. 203, 319–330.CrossRefGoogle Scholar
Gregorac, R. J. (1969), ‘On permutational products of groups’, J. Austral. Math. Soc. 10, 111–135.CrossRefGoogle Scholar
Mal'cev, A. I. (1949), ‘Nilpotent torsion-free groups’, Izv. Akad. Nauk SSSR Ser. Mat. 13, 201–212.Google Scholar
Neumann, B. H. (1960), ‘Permutational products of groups’, J. Austral. Math. Soc. 1, 299–310.CrossRefGoogle Scholar
Wiegold, J. (1959), ‘Nilpotent products of groups with amalgamations’, Publ. Math. Debrecen 6, 131–168.CrossRefGoogle Scholar
Wiegold, J. (1961), ‘Some remarks on generalised products of groups with amalgamations’, Math. Z. 75, 57–78.CrossRefGoogle Scholar