Brightest cluster galaxies (BCGs) residing in cool-core clusters are known to be the stage of intricate baryon cycle phenomena (e.g. gas inflows, AGN outflows, star formation feedback). The scenarios describing the observed properties of these galaxies are still controversial, suffering from limitations due to the spatial resolving power of the instruments, specifically for galaxies beyond the Local Universe. However, the dramatic improvements introduced by the integral-field unit instruments (e.g. MUSE) could shed light on the physical processes driving the evolution of these galaxies. We present an extensive analysis of the stellar and gas properties (i.e. kinematics, stellar mass, star formation rate) of the radio-loud BCG sitting at the centre of the X-ray luminous cool-core cluster Abell 2667 (z = 0.23), based on MUSE data. Our results indicate that the BCG is a massive elliptical, hosting an AGN that is possibly undergoing accretion of cold star-forming clouds of ICM or galactic cannibalism.

For decades, the deceptive simplicity of the radius 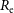$R_{\rm e}$, enclosing an arbitrary 50% of a galaxy’s light, has hamstrung the understanding of early-type galaxies (ETGs). Half a century ago, using these ‘effective half-light’ radii from de Vaucouleurs’ 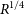$R^{1/4}$ model, Sérsic reported that bright ETGs follow the relation 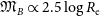$\mathfrak{M}_B\propto2.5\log R_{\rm e}$; and consequently, one has that 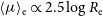$\langle\mu\rangle_{\rm e}\propto2.5\log R_{\rm e}$ and 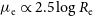$\mu_{\rm e}\propto2.5\log R_{\rm e}$, where 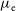$\mu_{\rm e}$ and 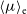$\langle\mu\rangle_{\rm e}$ are the effective surface brightness at 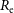$R_{\rm e}$ and the mean effective surface brightness within 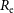$R_{\rm e}$, respectively. Sérsic additionally observed an apparent transition which led him to advocate for a division between what he called dwarf and giant ETGs; a belief frequently restated to occur at 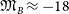$\mathfrak{M}_B \approx -18$ mag or 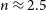$n\approx 2.5$. Here, the location of this false dichotomy in diagrams using ‘effective’ parameters is shown to change by more than 3 mag simply depending on the arbitrary percentage of light used to quantify a galaxy’s size. A range of alternative radii are explored, including where the projected intensity has dropped by a fixed percentage plus a battery of internal radii, further revealing that the transition at 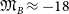$\mathfrak{M}_B\approx -18$ mag is artificial and does not demark a boundary between different physical processes operating on the ETG population.

The above understanding surrounding the effective radius 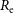$R_{\rm e}$ is of further importance because quantities such as dynamical mass 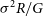$\sigma^2R/G$, gravitational-binding energy 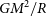$GM^2/R$, acceleration 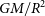$GM/R^2$, and the ‘Fundamental Plane’ also depend on the arbitrary percentage of light used to define R, with implications for dark matter estimates, galaxy formation theories, compact massive galaxies, studies of peculiar velocity flows, and more. Finally, some of the vast literature which has advocated for segregating the ETG population at 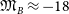$\mathfrak{M}_B \approx -18$ mag (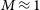$M\approx1$–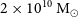$2\times10^{10}\,{\rm M}_{\odot}$) is addressed, and it is revealed how this pervasive mindset has spilled over to influence both the classical bulge versus pseudobulge debate and recently also correlations involving supermassive black hole masses.

Cosmological simulations predict that early-type galaxies (ETGs) are the results of extended mass accretion histories. The latter are characterized by different numbers of mergers, mergers’ mass ratios and gas fractions, and timing. Depending on the sequence and nature of these mergers that follow the first phase of the in-situ star formation, these accretion histories may lead to ETGs that have low or high mass halos, and that rotate fast or slow. Since the stellar halos maintain the fossil records of the events that led to their formation, a discontinuity may be in place between the inner regions of ETGs and their outer halos, because the time required for the halos’ stars to exchange their energies and momenta is very long compared with the age of these systems. Exquisite deep photometry and extended spectroscopy for significant samples of ETGs are then used to quantify the occurrence and significance of such a transition in the galaxies’ structural and kinematical parameters. Once this transition radius is measured, its dependency with the effective radius of the galaxies’ light distribution and total stellar masses can be investigated. Such correlations can then be compared with the predictions of accreted, i.e. ex-situ vs. in-situ components from cosmological simulations to validate such models.

We present preliminary results of the wide-field photometric study of the isolated elliptical galaxy NGC 1172, and its globular cluster system. Our data was obtained with the GMOS camera mounted on the Gemini South telescope, in the g′, r′, i′ and z′ bands. The aim of this work is to further our understanding of the evolution of NGC 1172, and to look for possible explanations for its unusual high specific frequency.

We present an analysis of the globular cluster system (GCS) of the galaxy NGC 3613, an intrinsically bright elliptical galaxy (MV = −21.5) in a low density environment (it is the central galaxy of a group of a dozen galaxies). Based on Gemini/GMOS photometry of NGC 3613 we obtained the following properties for this GCS. A ‘blue tilt’ is detected in the colour-magnitude diagram. The colour distribution is bimodal, presenting the two classical globular cluster (GC) sub-populations. The spatial and azimuthal projected distributions show that red sub-population correlates with the stellar component of the host galaxy.

Recent analyses of Lee et al. (2018, 2019) have confirmed that Galactic bulge consists of stellar populations originated from Milky Way globular clusters (MWGCs). Motivated by this, here we present the evolutionary population synthesis (EPS) for the Galactic bulge and early-type galaxies (ETGs) with the realistic treatment of individual variations in light elements observed in the MWGCs. We have utilized our model with GC-origin populations to explain the CN spread observed in ETGs, and the results show remarkable matches with the observations. We further employ our model to estimate the age of ETGs, which are considered as good analogs for the MW bulge. We find that, without the effect of our new treatments, EPS models will almost always underestimate the true age of ETGs. Our analysis indicates that the EPS with GC-origin populations is an essential constraint in determining the ETG formation epoch and is closely related to understanding the evolution of the Universe.

Based on very deep photometry, Surface Brightness Fluctuations (SBF) have been traditionally used to determine galaxy distances. We have recently computed SBF spectra of stellar populations at moderately high resolution, which are fully based on empirical stars. We show that the SBF spectra provide an unprecedented potential for stellar population studies that, so far, have been tackled on the basis of the mean fluxes. We find that the SBFs are able to unveil metal-poor stellar components at the one percent level, which are not possible to disentangle with the standard analysis. As these metal-poor components correspond to the first stages of the chemical enrichment, the SBF analysis provides stringent constrains on the quenching epoch.

Our multi-component photometric decomposition of the largest galaxy sample to date with dynamically-measured black hole masses nearly doubles the number of such galaxies. We have discovered substantially modified scaling relations between the black hole mass and the host galaxy properties, including the spheroid (bulge) stellar mass, the total galaxy stellar mass, and the central stellar velocity dispersion. These refinements partly arose because we were able to explore the scaling relations for various sub-populations of galaxies built by different physical processes, as traced by the presence of a disk, early-type versus late-type galaxies, or a Sérsic versus core-Sérsic spheroid light profile. The new relations appear fundamentally linked with the evolutionary paths followed by galaxies, and they have ramifications for simulations and formation theories involving both quenching and accretion.

In this work, we present preliminary results regarding the nuclear emission lines of a statistically complete sample of 56 early-type galaxies that are part of the Deep Integral Field Spectroscopy View of Nuclei of Galaxies (DIVING3D) Project. All early type galaxies (ETGs) were observed with the Gemini Multi-Object Spectrograph Integral Field Unit (GMOS-IFU) installed on the Gemini South Telescope. We detected emission lines in 93% of the sample, mostly low-ionization nuclear emission-line region galaxies (LINERs). We did not find Transition Objects nor H II regions in the sample. Type 1 objects are seen in ∼23% of the galaxies.

The surface-brightness profiles of galaxies I(R) and the density profiles of dark-matter halos ρ(r) are well represented by the same analytic function, named after either Sérsic, I∝e−(R/R*)1/m, or Einasto, ρ∝e−(r/r*)α, where R* and r* are characteristic radii. Systems with high Sérsic index m (or low Einasto index α) have steep central profiles and shallow outer profiles, while systems with low m (or high α) have shallow central profiles and steep profiles in the outskirts. We present the results of idealized numerical experiments which suggest that the origin of these profiles can be traced back to the initial density fluctuation field: high-α (low-m) systems form in smooth regions via few mergers, while low-α (high-m) systems form in clumpy regions via several mergers.

Early-type galaxies (ETGs) host a hot ISM produced mainly by stellar winds, and heated by Type Ia supernovae and the thermalization of stellar motions. High resolution 2D hydrodynamical simulations showed that ordered rotation in the stellar component results in the formation of a centrifugally supported cold equatorial disc. In a recent numerical investigation we found that subsequent generations of stars are formed in this cold disc; this process consumes most of the cold gas, leaving at the present epoch cold masses comparable to those observed. Most of the new stellar mass formed a few Gyrs ago, and resides in a disc.

Due to their environment isolated elliptical galaxies (IEs) should not be undergoing extant evolutionary processes yet many IEs have interacting dwarf companions, and where no merger remnants are visible IEs are often dynamically young. Furthermore, some IEs do not require dark matter to explain their dynamics. However, according to Cold Dark Matter (CDM) simulations all elliptical galaxies should be dark matter dominated, even if isolated, and IEs are much rarer in nature than predicted by CDM. Moreover, merging at the ~107 M⊙ level was recently discovered in the M31 system, showing that hierarchical merging may indeed be scale-free, as predicted by CDM. It seems a natural question to ask: what can IEs tell us about CDM? Here we analyse several IEs as probes of CDM. Our results spawn many new questions.

We summarise the HI properties of early-type galaxies, in particular the differences in HI morphologies observed in early-type galaxies of different luminosities. We find that in low-luminosity early-type galaxies the HI is almost always in a disk-like structure, with central surface densities high enough for star formation to occur. In a few luminous early-type galaxies the HI is also in a disk or in a ring-like structure, but in most luminous early-type galaxies the HI has a relatively irregular morphology. The surface densities in the HI disks in luminous early-type galaxies are lower than in the HI disks in low-luminosity early-type galaxies and no large-scale star formation should occur in these disks. We discuss these different HI characteristics in the context of other properties of early-type galaxies that correlate with luminosity.

We present the kpc-scale behaviour of the powerful extragalactic radio source Hercules A and the behaviour of the intracluster gas in which the radio source is situated. We have found that Hercules A exhibits a strong Laing-Garrington effect. The X-ray observations have revealed an extended X-ray emission elongated along the radio galaxy axis. The estimated temperature of the cluster is kT=2.45 keV and the central electron density is n○≃7.8×10−3 cm−3 which reveals a hot, dense environment in which Hercules A is situated. From the combined study of the radio and X-ray data we have estimated a central value of 3 ≲ B○(μG)≲9.

We also present the most recent results from the analysis of the radio data on the pc-scale structure of the radio galaxy, observed at 18 cm by the EVN–MERLIN array. A faint but compact radio source, coincident with the optical centre of Hercules A, was detected by the EVN at 18 mas resolution. The total flux density of the EVN core is 14.6 mJy. Its angular size is 18×7 mas with a position angle of ≃139°. There is also evidence for extended emission in the NW–SE direction, most probably from the eastern pc-scale jet. If this is true then there is a misalignment between the direction of the pc-eastern and the aligned kpc-scale jets of ≃35°.

We present H-band observations of the elliptical galaxy NGC 4696, the brightest member of the Centaurus cluster of galaxies. We have measured its light profile, using a two-dimensional fitting algorithm, out to a radius of 180 arcsec (37 h70−1 kpc). The profile is well described by a de Vaucouleurs law, with an effective radius of 35.3 ± 1.0 h70−1 kpc. There is no need for the extra free parameter allowed by a Sérsic law. Allowing for a variation of 0.3% in the sky level, the profile obtained is compatible with data from the Two-Micron All Sky Survey (2MASS). The profile shows no sign of either a truncation or an extended halo.

We assemble a sample of galaxy clusters whose brightest members are dumbbell galaxies and compare them with a control sample in order to investigate if they are the result of recent mergers. We show that the dumbbell sample is no more likely than other clusters to exhibit subclustering. However, they are much more likely to have at least one dumbbell component possessing a significant peculiar velocity with respect to the parent cluster than a non-dumbbell brightest cluster member. We interpret this in the context of seeing the clusters at various stages of post-merger relaxation.

We review our recent studies of the globular cluster system of NGC 5128. First, we have obtained low-resolution, high signal-to-noise spectroscopy of 72 globular clusters using Gemini-S/GMOS to obtain the ages, metallicities, and the level of alpha enrichment of the metal-poor and metal-rich globular cluster subpopulations. Second, we have explored the rotational signature and velocity dispersion of the galaxy's halo using over 560 globular clusters with radial velocity measurements. We have also compared the dependence of these properties on galactocentric distance and globular cluster age and metallicity. Using globular clusters as tracer objects, we have analyzed the mass, and mass-to-light ratio of NGC 5128. Last, we have measured the structural parameters, such as half-light radii, of over 570 globular clusters from a superb 1.2-square-degree Magellan/IMACS image. We will present the findings of these studies and discuss the connection to the formation and evolution of NGC 5128.

Surface Brightness Fluctuations (SBFs) are one of the most powerful techniques to measure the distance and to constrain the unresolved stellar content of extragalactic systems. For a given bandpass, the absolute SBF magnitude M depends on the properties of the underlying stellar population. Multi-band SBFs allow scientists to probe different stages of the stellar evolution: ultraviolet and blue wavelength band SBFs are sensitive to the evolution of stars within the hot horizontal branch and post-asymptotic giant branch phases, whereas optical SBF magnitudes explore the stars within the red giant branch and horizontal branch regimes. Near- and far-infrared SBF luminosities probe the important stellar evolution stage within the asymptotic giant branch and thermally pulsating asymptotic giant branch phases. Since the first successful application by Tonry and Schneider, a multiplicity of works have used this method to expand the distance scale up to 150 Mpc and beyond. This article gives a historical background of distance measurements, reviews the basic concepts of the SBF technique, presents a broad sample of investigations and discusses possible selection effects, biases, and limitations of the method. In particular, exciting new developments and improvements in the field of stellar population synthesis are discussed that are essential to understand the physics and properties of the populations in unresolved stellar systems. Further, promising future directions of the SBF technique are presented. With new upcoming space-based satellites such as Gaia, the SBF method will remain as one of the most important tools to derive distances to galaxies with unprecedented accuracy and to give detailed insights into the stellar content of globular clusters and galaxies.

Supermassive black holes (BHs) have been found in 75 galaxies by observing spatially resolved dynamics. The Hubble Space Telescope (HST) revolutionized BH work by advancing the subject from its ‘proof of concept’ phase into quantitative studies of BH demographics. Most influential was the discovery of a tight correlation between BH masses M• and the velocity dispersions σ of stars in the host galaxy bulge components at radii where the stars mostly feel each other and not the BH. Together with correlations between M• and bulge luminosity, with the ‘missing light’ that defines galaxy cores, and with numbers of globular clusters, this has led to the conclusion that BHs and bulges coevolve by regulating each other's growth. This simple picture with one set of correlations for all galaxies dominated BH work in the past decade.

New results are now replacing the above, simple story with a richer and more plausible picture in which BHs correlate differently with different kinds of galaxy components. BHs with masses of 105—106M⊙ live in some bulgeless galaxies. So classical (merger-built) bulges are not necessary equipment for BH formation. On the other hand, while they live in galaxy disks, BHs do not correlate with galaxy disks or with disk-grown pseudobulges. They also have no special correlation with dark matter halos beyond the fact that halo gravity controls galaxy formation. This leads to the suggestion that there are two modes of BH feeding, (1) local, secular and episodic feeding of small BHs in largely bulgeless galaxies that involves too little energy feedback to drive BH–host-galaxy coevolution and (2) global feeding in major galaxy mergers that rapidly grows giant BHs in short-duration events whose energy feedback does affect galaxy formation. After these quasar-like phases, maintenance-mode BH feedback into hot, X-ray-emitting gas continues to have a primarily negative effect in preventing late-time star formation when cold gas or gas-rich galaxies get accreted. Finally, the highest-mass galaxies inherit coevolution effects from smaller galaxies; the tightness of their BH correlations is caused mainly by averaging during dissipationless major mergers.

The presence of exponential bulges and anti-truncated disks has been noticed in many lenticular galaxies. In fact, it could be expected because the very formation of S0 galaxies includes various processes of secular evolution. We discuss how to distinguish between a pseudobulge and an anti-truncated disk, and also what particular mechanisms may be responsible for the formation of anti-truncated disks. Some clear examples of lenticular galaxies with a multi-tier exponential stellar structure are presented, – among them two central group giant S0s seen face-on and perfectly axisymmetric.