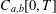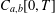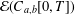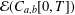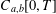1 results
A REPRESENTATION FOR THE INVERSE GENERALISED FOURIER–FEYNMAN TRANSFORM VIA CONVOLUTION PRODUCT ON FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 424-435
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
-
We study a representation for the inverse transform of the generalised Fourier–Feynman transform on the function space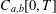
$C_{a,b}[0,T]$ which is induced by a generalised Brownian motion process. To do this, we define a transform via the concept of the convolution product of functionals on 
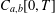$C_{a,b}[0,T]$. We establish that the composition of these transforms acts like an inverse generalised Fourier–Feynman transform and that the transforms are vector space automorphisms of a vector space 
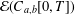${\mathcal{E}}(C_{a,b}[0,T])$. The vector space 
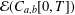${\mathcal{E}}(C_{a,b}[0,T])$ consists of exponential-type functionals on 
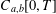$C_{a,b}[0,T]$.
