Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T19:56:27.808Z Has data issue: false hasContentIssue false
  • English
  • Français

A REPRESENTATION FOR THE INVERSE GENERALISED FOURIER–FEYNMAN TRANSFORM VIA CONVOLUTION PRODUCT ON FUNCTION SPACE

Part of: Set functions and measures on spaces with additional structure Harmonic analysis in several variables Markov processes

Published online by Cambridge University Press:  05 January 2017

SEUNG JUN CHANG  and
JAE GIL CHOI
SEUNG JUN CHANG
Affiliation:
Department of Mathematics, Dankook University, Cheonan 330-714, Republic of Korea email sejchang@dankook.ac.kr
JAE GIL CHOI*
Affiliation:
Department of Mathematics, Dankook University, Cheonan 330-714, Republic of Korea email jgchoi@dankook.ac.kr
*
✉jgchoi@dankook.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a representation for the inverse transform of the generalised Fourier–Feynman transform on the function space 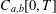$C_{a,b}[0,T]$ which is induced by a generalised Brownian motion process. To do this, we define a transform via the concept of the convolution product of functionals on 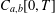$C_{a,b}[0,T]$. We establish that the composition of these transforms acts like an inverse generalised Fourier–Feynman transform and that the transforms are vector space automorphisms of a vector space 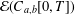${\mathcal{E}}(C_{a,b}[0,T])$. The vector space 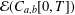${\mathcal{E}}(C_{a,b}[0,T])$ consists of exponential-type functionals on 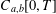$C_{a,b}[0,T]$.

Keywords

generalised Brownian motion processGaussian processexponential-type functionalgeneralised analytic Fourier–Feynman transformconvolution product

MSC classification

Primary: 28C20: Set functions and measures and integrals in infinite-dimensional spaces (Wiener measure, Gaussian measure, etc.)
Secondary: 42B10: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type 60J65: Brownian motion
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 424 - 435
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (2015R1C1A1A01051497) and the Ministry of Education (2015R1D1A1A01058224).

References

Brue, M. D., A Functional Transform for Feynman Integrals Similar to the Fourier Transform, PhD Thesis, University of Minnesota, Minneapolis, 1972.Google Scholar
Cameron, R. H. and Storvick, D. A., ‘An L 2 analytic Fourier–Feynman transform’, Michigan Math. J. 23 (1976), 1–30.CrossRefGoogle Scholar
Chang, S. J., Choi, J. G. and Skoug, D., ‘Integration by parts formulas involving generalized Fourier–Feynman transforms on function space’, Trans. Amer. Math. Soc. 355 (2003), 2925–2948.CrossRefGoogle Scholar
Chang, S. J., Lee, W. G. and Choi, J. G., ‘ L 2 -sequential transforms on function space’, J. Math. Anal. Appl. 421 (2015), 625–642.CrossRefGoogle Scholar
Chang, S. J. and Skoug, D., ‘Generalized Fourier–Feynman transforms and a first variation on function space’, Integral Transforms Spec. Funct. 14 (2003), 375–393.CrossRefGoogle Scholar
Choi, J. G. and Chang, S. J., ‘Generalized Fourier–Feynman transform and sequential transforms on function space’, J. Korean Math. Soc. 49 (2012), 1065–1082.CrossRefGoogle Scholar
Choi, J. G., Chung, H. S. and Chang, S. J., ‘Sequential generalized transforms on function space’, Abstr. Appl. Anal. 2013 565832 (2013), 12 pp.CrossRefGoogle Scholar
Huffman, T., Park, C. and Skoug, D., ‘Analytic Fourier–Feynman transforms and convolution’, Trans. Amer. Math. Soc. 347 (1995), 661–673.CrossRefGoogle Scholar
Huffman, T., Park, C. and Skoug, D., ‘Convolutions and Fourier–Feynman transforms of functionals involving multiple integrals’, Michigan Math. J. 43 (1996), 247–261.CrossRefGoogle Scholar
Huffman, T., Park, C. and Skoug, D., ‘Convolution and Fourier–Feynman transforms’, Rocky Mountain J. Math. 27 (1997), 827–841.CrossRefGoogle Scholar
Johnson, G. W. and Skoug, D. L., ‘An L p analytic Fourier–Feynman transform’, Michigan Math. J. 26 (1979), 103–127.CrossRefGoogle Scholar
Skoug, D. and Storvick, D., ‘A survey of results involving transforms and convolutions in function space’, Rocky Mountain J. Math. 34 (2004), 1147–1175.CrossRefGoogle Scholar
Yeh, J., ‘Singularity of Gaussian measures on function spaces induced by Brownian motion processes with non-stationary increments’, Illinois J. Math. 15 (1971), 37–46.CrossRefGoogle Scholar
Yeh, J., Stochastic Processes and the Wiener Integral (Marcel Dekker, New York, 1973).Google Scholar