We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Given two sets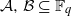 
of elements of the finite field 𝔽q of q elements, we show that the product set 
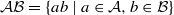contains an arithmetic progression of length k≥3 provided that k<p, where p is the characteristic of 𝔽q, and #𝒜#ℬ≥3q2d−2/k. We also consider geometric progressions in a shifted product set 𝒜ℬ+h, for f∈𝔽q, and obtain a similar result.
