Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:10:43.799Z Has data issue: false hasContentIssue false
  • English
  • Français

ARITHMETIC AND GEOMETRIC PROGRESSIONS IN PRODUCT SETS OVER FINITE FIELDS

Part of: Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  01 December 2008

IGOR E. SHPARLINSKI
IGOR E. SHPARLINSKI*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia (email: igor@ics.mq.edu.au)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given two sets 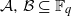of elements of the finite field 𝔽q of q elements, we show that the product set 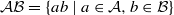contains an arithmetic progression of length k≥3 provided that k<p, where p is the characteristic of 𝔽q, and #𝒜#ℬ≥3q2d−2/k. We also consider geometric progressions in a shifted product set 𝒜ℬ+h, for f∈𝔽q, and obtain a similar result.

Keywords

arithmetic progressionsgeometric progressionsproduct setscharacter sums

MSC classification

Secondary: 11T30: Structure theory 11T23: Exponential sums
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 78 , Issue 3 , December 2008 , pp. 357 - 364
Copyright
Copyright © 2009 Australian Mathematical Society

References

[1]Ahmadi, O. and Shparlinski, I. E., ‘Geometric progressions in sum sets over finite fields’, Monatsh. Math. 152 (2007), 177–185.CrossRefGoogle Scholar
[2]Croot, E. and Borenstein, E., ‘Geometric progressions in thin sets’, Preprint, 2006.Google Scholar
[3]Croot, E., Ruzsa, I. Z. and Schoen, T., ‘Arithmetic progressions in sparse sumsets’, in: Combinatorial Number Theory (Walter de Gruyter, Berlin, 2007), pp. 157–164.Google Scholar
[4]Green, B. J., ‘Arithmetic progressions in sumsets’, Geom. Funct. Anal. 3 (2002), 584–597.CrossRefGoogle Scholar
[5]Green, B. and Tao, T., ‘The primes contain arbitrarily long arithmetic progressions’, Ann. of Math. 167 (2008), 481–547.CrossRefGoogle Scholar
[6]Ismoilov, D., ‘Estimates of complete character sums of polynomials’, Proc. Steklov Math. Inst., Moscow 200 (1992), 171–184 (in Russian).Google Scholar
[7]Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
[8]Ruzsa, I. Z., ‘Arithmetic progressions in sumsets’, Acta Arith. 60 (1991), 191–202.CrossRefGoogle Scholar
[9]Tao, T. and Vu, V., Additive Combinatorics (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar