1 results
An analysis of the effect of ghost force oscillation on quasicontinuum error
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 43 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 08 April 2009, pp. 591-604
- Print publication:
- May 2009
-
- Article
- Export citation
-
The atomistic to continuum interface for quasicontinuum energiesexhibits nonzero forces under uniform strain that have beencalled ghost forces.In this paper,we prove for a linearization of a one-dimensional quasicontinuum energyaround a uniform strainthat the effect of the ghost forces on the displacementnearly cancels and has a small effect on the error away from the interface.We give optimal order error estimatesthat show that the quasicontinuum displacementconverges to the atomistic displacement at the rate O(h)in the discrete $\ell^\infty$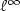
andw 1,1 norms where h is the interatomic spacing.We also give a proof that the error in the displacement gradientdecays away from the interface to O(h) at distance O(h|logh|)in the atomistic region and distance O(h) in the continuum region.Our work gives an explicit and simplified form for the decay of the effect of theatomistic to continuum coupling error in terms of a general underlying interatomic potential and gives the estimates described above in the discrete $\ell^\infty$ 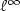and w1,p norms.
