Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T14:55:16.163Z Has data issue: false hasContentIssue false
  • English
  • Français

An analysis of the effect of ghost force oscillation on quasicontinuum error

Published online by Cambridge University Press:  08 April 2009

Matthew Dobson  and
Mitchell Luskin
Matthew Dobson
Affiliation:
School of Mathematics, University of Minnesota, 206 Church Street SE Minneapolis, MN 55455, USA. dobson@math.umn.edu; luskin@umn.edu
Mitchell Luskin
Affiliation:
School of Mathematics, University of Minnesota, 206 Church Street SE Minneapolis, MN 55455, USA. dobson@math.umn.edu; luskin@umn.edu
Get access

Abstract

The atomistic to continuum interface for quasicontinuum energiesexhibits nonzero forces under uniform strain that have beencalled ghost forces.In this paper,we prove for a linearization of a one-dimensional quasicontinuum energyaround a uniform strainthat the effect of the ghost forces on the displacementnearly cancels and has a small effect on the error away from the interface.We give optimal order error estimatesthat show that the quasicontinuum displacementconverges to the atomistic displacement at the rate O(h)in the discrete $\ell^\infty$ 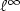andw 1,1 norms where h is the interatomic spacing.We also give a proof that the error in the displacement gradientdecays away from the interface to O(h) at distance O(h|logh|)in the atomistic region and distance O(h) in the continuum region.Our work gives an explicit and simplified form for the decay of the effect of theatomistic to continuum coupling error in terms of a general underlying interatomic potential and gives the estimates described above in the discrete $\ell^\infty$ 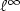and w1,p norms.

Keywords

Quasicontinuumatomistic to continuumghost force.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 43 , Issue 3 , May 2009 , pp. 591 - 604
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arndt, M. and Luskin, M., Goal-oriented atomistic-continuum adaptivity for the quasicontinuum approximation. Int. J. Mult. Comp. Eng. 5 (2007) 407–415. CrossRef
Arndt, M. and Luskin, M., Error estimation and atomistic-continuum adaptivity for the quasicontinuum approximation of a Frenkel-Kontorova model. Multiscale Model. Simul. 7 (2008) 147–170. CrossRef
Arndt, M. and Luskin, M., Goal-oriented adaptive mesh refinement for the quasicontinuum approximation of a Frenkel-Kontorova model. Comp. Meth. App. Mech. Eng. 197 (2008) 4298–4306. CrossRef
Badia, S., Parks, M.L., Bochev, P.B., Gunzburger, M. and Lehoucq, R.B., On atomistic-to-continuum (AtC) coupling by blending. Multiscale Model. Simul. 7 (2008) 381–406. CrossRef
Blanc, X., Le Bris, C. and Legoll, F., Analysis of a prototypical multiscale method coupling atomistic and continuum mechanics. ESAIM: M2AN 39 (2005) 797–826. CrossRef
Curtin, W. and Miller, R., Atomistic/continuum coupling in computational materials science. Model. Simul. Mater. Sc. 11 (2003) R33–R68. CrossRef
Dobson, M. and Luskin, M., Analysis of a force-based quasicontinuum method. ESAIM: M2AN 42 (2008) 113–139. CrossRef
W. E and P. Ming. Analysis of the local quasicontinuum method, in Frontiers and Prospects of Contemporary Applied Mathematics, T. Li and P. Zhang Eds., Higher Education Press, World Scientific (2005) 18–32.
W. E., J. Lu and J. Yang, Uniform accuracy of the quasicontinuum method. Phys. Rev. B 74 (2006) 214115. CrossRefPubMed
Knap, J. and Ortiz, M., An analysis of the quasicontinuum method. J. Mech. Phys. Solids 49 (2001) 1899–1923. CrossRef
Lin, P., Theoretical and numerical analysis for the quasi-continuum approximation of a material particle model. Math. Comp. 72 (2003) 657–675 (electronic). CrossRef
Lin, P., Convergence analysis of a quasi-continuum approximation for a two-dimensional material. SIAM J. Numer. Anal. 45 (2007) 313–332. CrossRef
Miller, R. and Tadmor, E., The quasicontinuum method: Overview, applications and current directions. J. Comput. Aided Mater. Des. 9 (2002) 203–239. CrossRef
Miller, R., Shilkrot, L. and Curtin, W.. A coupled atomistic and discrete dislocation plasticity simulation of nano-indentation into single crystal thin films. Acta Mater. 52 (2003) 271–284. CrossRef
P. Ming and J.Z. Yang, Analysis of a one-dimensional nonlocal quasicontinuum method. Preprint.
Oden, J.T., Prudhomme, S., Romkes, A. and Bauman, P., Multi-scale modeling of physical phenomena: Adaptive control of models. SIAM J. Sci. Comput. 28 (2006) 2359–2389. CrossRef
C. Ortner and E. Süli, A-posteriori analysis and adaptive algorithms for the quasicontinuum method in one dimension. Research Report NA-06/13, Oxford University Computing Laboratory (2006).
Ortner, C. and Süli, E., Analysis of a quasicontinuum method in one dimension. ESAIM: M2AN 42 (2008) 57–91. CrossRef
Parks, M.L., Bochev, P.B. and Lehoucq, R.B., Connecting atomistic-to-continuum coupling and domain decomposition. Multiscale Model. Simul. 7 (2008) 362–380. CrossRef
Prudhomme, S., Bauman, P.T. and Error, J.T. Oden control for molecular statics problems. Int. J. Mult. Comp. Eng. 4 (2006) 647–662. CrossRef
Rodney, D. and Phillips, R., Structure and strength of dislocation junctions: An atomic level analysis. Phys. Rev. Lett. 82 (1999) 1704–1707. CrossRef
Shenoy, V., Miller, R., Tadmor, E., Rodney, D., Phillips, R. and Ortiz, M., An adaptive finite element approach to atomic-scale mechanics – the quasicontinuum method. J. Mech. Phys. Solids 47 (1999) 611–642. CrossRef
Shimokawa, T., Mortensen, J., Schiotz, J. and Jacobsen, K., Matching conditions in the quasicontinuum method: Removal of the error introduced at the interface between the coarse-grained and fully atomistic regions. Phys. Rev. B 69 (2004) 214104. CrossRef
G. Strang and G. Fix, Analysis of the Finite Elements Method. Prentice Hall (1973).
Tadmor, E., Ortiz, M. and Phillips, R., Quasicontinuum analysis of defects in solids. Phil. Mag. A 73 (1996) 1529–1563. CrossRef